Течение жидкости в трубопроводах с местными сопротивлениями
Местными сопротивлениями называются места изменения формы и размеров канала, в которых поток деформируется – расширяется, сужается, искривляется.
Уравнения сохранения для течений с местными сопротивлениями имеют тот же вид, что и для течений с трением, только вместо работы сил трения или потерь давления необходимо подставлять работу на преодоление местных сопротивлений. Если расчет ведется с учетом потерь на трение, то полные потери Dрп должны складываться из потерь на трение Dртр и местных потерь Dрм.
Потери давления, происходящие в местных сопротивлениях, выражаются формулой Вейсбаха
,
где xм – безразмерный коэффициент местного сопротивления, отнесенный к скорости за или перед местным сопротивлением; u – средняя скорость потока в сечении, расположенном за или перед местным сопротивлением.
Таким образом, потери давления на трение и в местных сопротивлениях выражаются формулой
.
Значения коэффициента xм зависят от формы местного сопротивления, его геометрических параметров и числа Рейнольдса.
Можно считать, что при турбулентном режиме течения коэффициент местных сопротивлений от числа Рейнольдса не зависит и, следовательно, потери давления пропорциональны квадрату скорости (квадратичный режим сопротивления). При ламинарном режиме считают, что
,
где А – число, определяемое формой местного сопротивления; xкв – коэффициент местного сопротивления при квадратичном режиме сопротивления.
|
|
|
Значения коэффициентов местного сопротивления приводятся в справочной литературе и в приложении 1.
При расчете газовых потоков иногда для оценки гидродинамических потерь удобнее вместо коэффициента потерь пользоваться коэффициентом сохранения полного давления.
Если идеально затормозить газовый поток, т. е. уменьшить скорость течения до нуля изоэнтропийным путем, то давление газа станет равным полному давлению или давлению стационарно заторможенного потока р*. Если на участке потока 1-2 наблюдаются потери, то полное давление 
в сечении 2 будет ниже полного давления 
в сечении 1, а коэффициент сохранения полного давления вычисляется по формуле
.
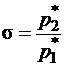Кроме того, из-за потерь на участке 1-2 скорость потока, а также приведенная скорость l будет меньше, чем при течении без потерь. Это несоответствие учитывается коэффициентом скорости
,
где lт – приведенная скорость в расчетном сечении (сечение 2), определяемая по статическому давлению в этом сечении и полному давлению в базовом сечении (сечение 1).
Зная lт, можно определить коэффициент скорости
и затем определить s
.
ПРИМЕР
Воздух всасывается по трубе из окружающей среды. Показания вакуумметра, установленного на трубе Dpв = 2500 Па. Коэффициент сопротивления входной части трубы до места присоединения вакуумметра xм = 0,1. Плотность воздуха 1,25 кг/м3. Определить скорость воздуха в трубе.
|
|
|
Решение
Напишем уравнение Бернулли для двух сечений, первое из которых относиться к окружающей среде, а второе в месте установки вакуумметра. Судя по небольшой величине разрежения в трубе, плотность газа можно принять постоянной.
.
В окружающей среде u1 = 0, разность уровней давлений p2 – p1 равна показаниям вакуумметра. Поэтому
,
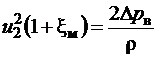откуда скорость воздуха в трубе
.
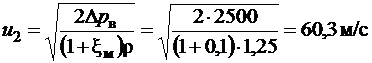ЗАДАЧИ
Задача 2.3.1. В качестве нагревательных приборов системы отопления использованы трубы диаметром d1 = 0,1 м (рис. 2.12). Стояк, подводящий нагретую воду и соединительные линии, выполнены из труб диаметром d2 = 0,025 м и приварены к торцам нагревательных труб. Определить потери давления при внезапном расширении трубопроводов, если скорость движения горячей воды в подводящих линиях равна 0,3 м/с, а температура воды 70° С. Кинематическая вязкость и плотность воды n = 0,37×10-6 м2/с, r = 972 кг/м3.
Рис. 2.12
Задача 2.3.2. Для ограничения расхода воды в водопроводной линии установлена диафрагма. Избыточные давления в трубе до и после диафрагмы равны соответственно 6,37×104 Па и 2,05×104 Па. Диаметр трубы равен 0,076 м. Определить необходимый диаметр отверстия диафрагмы с таким расчетом, чтобы расход в линии был равен 0,006 м3/с.
|
|
|
Задача 2.3.3. Вода протекает по горизонтальной трубе, внезапно сужающейся от диаметра 0,2 м до диаметра 0,1 м. Расход воды равен 0,02 м3/с. Определить, какую разность уровней ртути покажет дифференциальный манометр, включенный в месте изменения сечения. Температура воды 20° С.
Задача 2.3.4. Определить потери давления при движении масла в радиаторе, если расход масла равен 0,0004 м3/с. Диаметр коллектора радиатора равен 0,03 м, диаметр трубок 0,01 м, длина их 1 м. Плотность масла 900 кг/м3, кинематическая вязкость масла равна
6,5×10-5 м2/с.
Задача 2.3.5. Определить избыточное давление, создаваемое насосом системы охлаждения двигателя и абсолютное давление перед входом в насос (рис. 2.13). Клапан, установленный в крышке радиатора срабатывает при избыточном давлении 5 кПа. Длина верхнего патрубка равна 0,3 м, нижнего – 0,4 м. Диаметр патрубков равен
0,04 м. Коэффициенты потерь, приведенные к скорости в патрубках, равны: блока цилиндров – 3,5; термостата – 2,5; радиатора – 1,5. Расход жидкости в системе охлаждения составляет 4 л/с.
|
|
|
Рис. 2.13
Задача 2.3.6. Определить коэффициент сопротивления жиклера, установленного в канале диаметром 10 мм, если число Рейнольдса потока жидкости в канале равно 100 (рис. 2.14).
Рис. 2.14
Задача 2.3.7. Определить диаметр топливного жиклера карбюратора, обеспечивающего при расходе воздуха 7 кг/ч коэффициент избытка воздуха в топливо-воздушной смеси a = 1 (Gв/Gт = 15). Воздух считать несжимаемым плотностью 1,2 кг/м3. Принять следующие коэффициенты сопротивления, отнесенные к скорости во входящем патрубке воздушного фильтра: фильтрующего элемента xф = 3; диффузора карбюратора xк = 0,1 (рис. 2.15).
Рис. 2.15
Дата добавления: 2018-02-15; просмотров: 1103; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!