Уравнения сохранения для идеальной жидкости
Основные уравнения сохранения для двух сечений потока, позволяющие решать простейшие задачи, получают интегрированием уравнений сохранения. Для задач, в которых не учитываются потери в местных сопротивлениях и на преодоление трения, а также отсутствует техническая работа, уравнения сохранения имеют следующий вид:
уравнение неразрывности
 ;
;
уравнение энергии
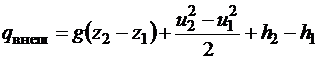 ;
;
уравнение Бернулли
 .
.
При расчете течения газа часто пренебрегают изменением потенциальной энергии g(z2 – z1) вследствие ее малости.
В случае, когда плотность жидкости на участке 1-2 меняется незначительно или жидкость считается несжимаемой, интеграл в уравнении Бернулли равен
 .
.
В изобарическом процессе изменения состояния газа интеграл равен нулю:
 .
.
В изотермическом процессе
 .
.
Если состояние газа изменяется по идеальной адиабате, то
 .
.
Уравнение сохранения количества движения при отсутствии трения после интегрирования уравнения (1.4) имеет вид
 .
.
При решении задач часто используются еще и другие уравнения: уравнение Менделеева-Клапейрона, связывающее основные термодинамические параметры идеального газа

и уравнение адиабаты
 .
.
ПРИМЕР
Идеальная сжимаемая жидкость течет по горизонтальной трубе переменного поперечного сечения. В некотором сечении площадью F1 известны все параметры потока: скорость u1, давление p1, плотность r1. Определить параметры потока в сечении с площадью F2, считая процесс течения адиабатным.
|
|
|
Решение
В случае адиабатного течения и неизменной потенциальной энергии g(z2 – z1) уравнение Бернулли имеет вид
 .
.
Запишем еще уравнение сохранения массы
 .
.
В этих двух уравнениях три неизвестные: u2, p2, и r2, поэтому добавим третье уравнение – уравнение адиабаты:
 .
.
Решая совместно три уравнения, находим параметры во втором сечении.
ЗАДАЧИ
Задача 2.1.1. Вентилятор всасывает атмосферный воздух через кольцевую трубу с внутренним диаметром d = 150 мм и внешним диаметром D = 300 мм (рис. 2.1). Статическое давление воздуха в трубе измеряется с помощью водяного дифференциального манометра, причем разность уровней равна H = 280 мм. Атмосферное давление p0 = 0,1 МПа, температура воздуха T0 = 293 K. Определить расход воздуха через кольцевую трубу.

Рис. 2.1
Задача 2.1.2. Камера смешения представляет собой трубу диаметром d. В начальном сечении 1-1 известно распределение скорости и температуры воздуха: в кольцевой части (0,5d0 < d < d0) скорость воздуха u1 = 100 м/с, температура Т1 = 300 К; в центральной части
(d < 0,5d0) скорость воздуха u1' = 220 м/с, температура Т1' = 400 К. Статическое давление р1 = 0,1 МПа постоянно по сечению. В выходном сечении 2-2 поток выравнивается, т. е. имеет постоянные по сечению значения скорости u2, температуры T2 и давления p2. Определить u2, T2 и p2. Трением пренебречь.
|
|
|
Задача 2.1.3. На трубопровод диаметром 350 мм установлен расходомер типа трубы Вентури с диаметром узкого сечения 225 мм (рис. 2.2). По трубопроводу перекачивается воздух при давлении
105 Па и температуре 370 K. Определить разность давлений, которую покажет заполненный водой U-образный манометр, подключенный к расходомеру, если через трубу проходит 20 кг/с воздуха. Потери не учитывать.

Рис. 2.2
Задача 2.1.4. Определить расход воздуха через карбюратор, при котором начнется подача в диффузор топлива из поплавковой камеры (рис. 2.3). Уровень топлива в поплавковой камере находится на 3 мм ниже выходного отверстия распылителя. Плотность топлива r =
= 740 кг/м3, диаметр диффузора d = 25 мм.

Рис. 2.3
Задача 2.1.5. Скорость воздушного потока равна 200 м/с, температура торможения равна 400 К. Определить статическую температуру в потоке.
Задача 2.1.6. Уровень воды в водонапорном баке 1 превышает уровень воды в трубопроводе на величину Н = 2 м (рис. 2.4). Вода течет по трубопроводу диаметром d1 = 50 мм. На трубопроводе имеется сужение 2 диаметром d2 = 40 мм, к которому присоединена трубка 3, опущенная в резервуар 4. Уровень воды в резервуаре 4 ниже уровня воды в трубопроводе на величину h = 1 м. Определить направление движения воды в трубке 3. Трением пренебречь.
|
|
|

Рис. 2.4
Задача 2.1.7. Воздух вытекает из камеры через трубопровод с площадью выходного сечения 300 см2 (рис. 2.5). Давление в камере равно 0,15 МПа, а температура – 1500 К. Найти реактивную силу. Трением и местными потерями пренебречь.

Рис. 2.5
Задача 2.1.8. Вода вытекает из большого закрытого бака в атмосферу (р0 = 0,1 МПа) через сопло с выходной площадью 10 см2. Высота воды в баке над соплом 12 м. Над уровнем воды в баке давление равно 0,5 МПа. Определить расход воды через сопло.
Задача 2.1.9. Жидкость вытекает из трубы с диаметром d, на конце которой укреплена круглая шайба 1 диаметром D (рис. 2.6). На расстоянии H = d/4 от шайбы помещен диск 2 того же диаметра D. Жидкость, выходящая из трубы растекается радиально между двумя плоскостями и затем выходит в атмосферу. Расход и плотность жидкости заданы. Найти закон изменения давления вдоль радиуса диска, считая жидкость идеальной. Принять течение радиальным и безотрывным.

Рис. 2.6
Задача 2.1.10. Трубопровод переменного сечения смонтирован в вертикальной плоскости. В сечении 1-1 диаметр трубопровода равен d1 = 150 мм, а давление равно р1 = 0,12 МПа. Сечение 2-2 находится выше сечения 1-1 на 7 м и имеет диаметр d2 = 250 мм, а давление в нем р2 = 0,1 МПа. По трубопроводу перекачивается керосин с плотностью r = 830 кг/м3. В каком направлении движется жидкость по трубопроводу при расходе 0,2 м3/с?
|
|
|
Течение жидкости с трением
Будем рассматривать установившееся течение в трубе постоянного поперечного сечения при наличии трения, но без теплообмена с внешней средой.
Уравнение Бернулли в этом случае имеет вид
 .
.
Работа сил трения на участке длиной dx определяется по выражению
 ,
,
где lтр – коэффициент потерь на трение в трубе; dэ – эквивалентный диаметр трубы.
Эквивалентный диаметр рассчитывается по формуле
dэ = 4F/П,
где П – смоченный периметр сечения трубы.
Уравнение неразрывности в этом случае (F = const) имеет следующий вид:
ru = const
или в дифференциальной форме
 .
.
Преобразуя приведенные выше уравнения, можно получить для газов следующую формулу:
 ,
,
где l – приведенная скорость потока.
Приближенно полагают lтр = const. В этом случае последнее уравнение легко интегрируется:
 .
.
Для несжимаемой жидкости уравнение Бернулли при течении с трением имеет вид
 .
.
Потери давления на трение по длине трубопровода l определяются по формуле Дарси-Вейсбаха
 ,
,
где uср – средняя скорость потока по длине l.
Коэффициент трения lтр зависит от режима течения (числа Рейнольдса), относительной шероховатости стенки и формы поперечного сечения трубопровода (рис. 2.7).

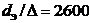




Рис. 2.7
Числа Рейнольдса является безразмерным критерием, характеризующим режим течения
 ,
,
где n – кинематическая вязкость жидкости (см. приложение 1).
При ламинарном режиме течения, т. е. при Re < 2300, коэффициент lтр зависит от числа Рейнольдса и формы поперечного сечения трубы
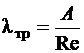 ,
,
где А – коэффициент, зависящий от формы поперечного сечения трубы (см. приложение 1).
При турбулентном режиме течения, т.е. при Re > 4 000 для технически гладких труб шероховатость поверхности на сопротивление не влияет. В этом случае при Re < 105 коэффициент трения lтр определяется по формуле Блазиуса
 ,
,
а при Re > 105 по формуле
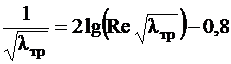 .
.
Для шероховатых труб коэффициент трения lтр может определяться по следующей формуле:
 ,
,
где D – эквивалентная равномерно-зернистая абсолютная шероховатость поверхности трубы.
Уравнение количества движения при течении с трением имеет вид
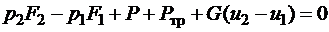 .
.
ПРИМЕР
По горизонтальному трубопроводу диаметром d = 0,01 м течет вода, имеющая в первом сечении следующие параметры: u1 = 10 м/c, p1 = = 1,5 МПа и Т1 = 293 К. Определить давление в сечении, отстоящем на расстоянии 2 м от первого сечения ниже по потоку, если относительная шероховатость поверхности трубы равна 0,003, а плотность воды 998 кг/м3.
Решение
Запишем уравнение Бернулли для несжимаемой жидкости

и уравнение сохранения массы
r1u1F1 = r2u2F2.
Поскольку воду можно считать несжимаемой, т. е. r1 = r2, а площадь трубопровода постоянна (F1 = F2), то
u1 = u2,
и уравнение Бернулли упрощается
 .
.
Отсюда
 .
.
Для определения коэффициента потерь вычислим число Рейнольдса
 .
.
Кинематическая вязкость воды при Т = 293 К n = 1,01×10-6 м2/с. Тогда
 .
.
Так как режим течения турбулентный (Re > 4 000), то lтр определим по формуле для шероховатых труб
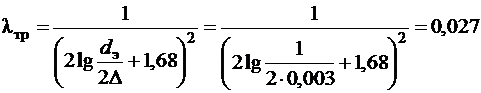 .
.
Давление во втором сечении
 .
.
ЗАДАЧИ
Задача 2.2.1. Вентиляционная труба диаметром d = 0,1 м имеет длину l = 100 м. Определить давление, которое должен развивать вентилятор и мощность электродвигателя, если расход воздуха, подаваемого по трубе Q = 0,078 м3/с, а КПД вентилятора h = 0,6. Давление окружающей среды 0,1 МПа, температура 20° С. Относительная шероховатость поверхности трубы 0,002. Местных сопротивлений нет.
Задача 2.2.2. Вода вытекает их верхнего резервуара в нижний через отверстие в дне резервуара (рис. 2.8). Каким способом и во сколько раз можно увеличить расход жидкости, не меняя диаметра отверстия и напора воды Н1. Размеры Н1 = 0,5 м, Н2 = 1,5 м. Местными потерями пренебречь.

Рис. 2.8
Задача 2.2.3. Определить максимально возможную секундную утечку жидкости через зазор между насосным плунжером и цилиндром при давлении Dp = 25 МПа, если диаметр плунжера равен d =
= 20 мм, а радиальный зазор при соосном расположении плунжера и цилиндра равен d = 0,01 мм (рис. 2.9). Длина зазора l = 30 мм, вязкость жидкости n = 1×10-6 м2/с, плотность жидкости r = 800 кг/м3.

Рис. 2.9
Задача 2.2.4. Определить расход воды из напорного бака с учетом потерь на трение (рис. 2.10). Трубы технически гладкие. Давление окружающей среды равно 0,1 МПа, давление в баке рб =
= 0,15 МПа. Размеры: H = 3 м, l1 = 2 м, l2 = 1,5 м, D = 0,04 м, d =
= 0,03 м.

Рис. 2.10
Задача 2.2.5. Расход воды при температуре 10° С в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб (абсолютная шероховатость D =
= 0,15 мм) равен 0,075 м3/с. Внутренняя труба имеет наружный диаметр d = 0,075 м, а наружная труба имеет внутренний диаметр D =
0,1 м. Найти потери давления на трение по длине трубы l = 300 м.
Задача 2.2.6. Определить потери давления в магистралях гидропередач, если расходы жидкости Q1 = 0,0001 м3/с, Q2 = 0,0002 м3/с, диаметры трубопроводов d1 = 0,005 м, d2 = 0,01 м, длины l1 = 1 м, l2 = 2 м, плотность жидкости r = 900 кг/м3, кинематическая вязкость
n = 6,5×10-5 м2/с (рис. 2.11).

Рис. 2.11
Задача 2.2.7. Определить диаметр нового стального трубопровода длиной 1000 м, который должен пропускать расход воды 0,02 м3/с при потерях давления 0,02 МПа. Температура подаваемой воды 20° С.
Дата добавления: 2018-02-15; просмотров: 2828; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
