Теплоотдача в ограниченном пространстве
Процесс рассчитывается по уравнениям теплопроводности, но при этом вводится понятие эквивалентной теплопроводности
lэкв = lж × eк,
где: e- коэффициент конвекции, который учитывает влияние конвекции. При вычислении чисел подобия за определяющий размер принята толщина зазора d, а за определяющую температуру средняя температура tср = (tc1 +tc2)/2
если Gr × Pr < 103, то eк = 1
если 103 <Gr × Pr< 106, то eк = 0.105 × Grs,ср0.3 × Prср0.3
если 106 <Gr × Pr< 1010, то eк = 0.4 × Grs,ср0.2 × Prср0.2
Вынужденная конвекция
Теплоотдача при омывании плоской поверхности
Характерный размер - длина поверхности в направлении движения потока l или расстояние x от входной кромки до точки, в которой определяется значение локального коэффициента теплоотдачи. Определяющая температура - температура потока tж.
Если Re < 5×105, то для определения локального коэффициента используется уравнение:
Nuхж = 0.33 × Reхж0.55 × Prж0.33 ×(Prж / Prс)0.25
среднего коэффициента теплоотдачи :
Nulж = 0.66 × Relж0.5 × Prж0.33 × (Prж / Prс)0.25
Для воздуха Nulж = 0.57 × Relж0.5
если Re > 5 × 105 то для определения локального коэффициента теплоот-
дачи
Nuхж = 0.03 × Reхж0.2 × × Prж0.43 × (Prж / Prc)0.25
среднего
Nuхж = 0.037 × Reхж0.8 ×× Prж0.43 ×(Prж / Prc)0.25
для воздуха
Nulж = 0.032 × Relж0.8
Теплоотдача при течении жидкости в трубах
Характерный размер - внутренний диаметр трубы. Если канал не круглого сечения, то dпр = 4 × S / P, где S - площадь сечения канала, м2, P - периметр, м. Определяющая температура tж - температура потока. Если труба согнута в змеевик, то вводится поправка eR, значение которой рассчитывается по формуле:
|
|
|
eR = 1 + 1.77 dт / R з
где dт - диаметр трубы, м; Rз - радиус змеевика, м.
При 10 < Re < 104 и l / d > 10
Nudж = 1,4 * (Redж ×(d/l))0.4 × Prж0.33 × (Prж / Prс)0.25 eR
при Re > 104
Nudж = 0,021 × Redж0.8 × Prж0.43 × (Prж / Prс)0.25 eR
для воздуха Nudж = 0,018 × Redж0.8
где el - учитывает изменение коэффициента теплоотдачи от длины трубы, если l/d > 50, то el = 1, остальные значения можно найти из табл.1
Таблица 1
Значения поправочного коэффициента el
| Redж | Отношение длины трубы к ее диаметру l /d | ||||||||
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 104 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 5×104 | 1,34 | 1,27 | 1,18 | 1,13 | 1,10 | 1,08 | 1,04 | 1,02 | 1 |
| 105 | 1,28 | 1,22 | 1,15 | 1,10 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 106 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Теплоотдача при поперечном омывании труб
Одиночная труба.
Характерный размер - наружный диаметр трубы d, определяющая температура - температура потока tж.
Если Redж < 105, Nudж=0.56 × Redж0.5× Prж0.36×(Prж /Prc)0.25× ey
Для воздуха : Nudж=0.49 × Redж0.25 × ey
При Redж >105 Nudж=0.28 ××Redж0.6 × Prж 0.3 ×(Prж/Prc )0.25× ey
|
|
|
Для воздуха Nudж = 0.245× Redж0.6 × ey
ey- поправочный коэффициент, учитывающий угол атаки y значение которого можно найти в табл.2
Таблица 2
Значения поправочного коэффициента ey
| Поправочный | Угол атаки, y | ||||||||
| коэффициент | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 |
| ey | 1 | 1 | 0.98 | 0.94 | 0.88 | 0.78 | 0.67 | 0.52 | 0.42 |
Пучки труб: Коридорные пучки
При Redж < 103 Nudж = 0.56 × Redж0.5 × Prж0.36 × (Prж / Prс)0.25× ey × eS
для воздуха Nudж = 0.49 × Redж0.5 × ey× eS
При Redж < 103 Nudж = 0.22 × Redж0.65 × Prж0.3 ×(Prж / Prс)0.25 × ey× eS
для воздуха Nudж = 0.194 × Redж0.65 × ey × eS ,
где eS - поправочный коэффициент, учитывающий влияние относительных шагов.
eS= (S2 / d)-0.15
где S2 - расстояния между рядами труб в пучке.
Шахматные пучки
При Re < 103 Nudж = 0.56 × Redж0.5 × Prж0.36 × (Prж / Prс)0.25 × ey × eS1
для воздуха Nudж = 0.49 × Redж0.5 × ey × eS1
При Rc < 103 Nudж = 0.4 × Redж0.6 × Prж0.36 × (Prж / Prс)0.25 × ey × eS1
для воздуха Nudж = 0.35 × Redж0.6,
где eS1 - поправочный коэффициент, учитывающий расстояние между трубами в пучке.
Если S1 / S2 < 2, то eS1 = (S1 / S2)1/6
Если S1 / S2 >=2, то eS1 = 1,12
где S1 - расстояние между трубами в ряду, а S2 - расстояние между рядами ;
|
|
|
Примеры решения задач
Задача 1
Определить средний коэффициент теплоотдачи в поперечном потоке воздуха для трубы диаметром d = 20 мм, если температура воздуха tЖ = 30°С, а скорость W = 5 м/с.
Решение
При tЖ = 30°С, lЖ = 0,0267 Вт/(м×К), n = 16,0×10-6 м2/с,
 . Re > Reкрит.
. Re > Reкрит.
Режим движения турбулентный, следовательно, уравнение подобия имеет вид
 ;
;
так как  , то отсюда
, то отсюда  .
.
Задача 2
Определить средний коэффициент теплоотдачи для восьмирядного коридорного пучка труб, состоящего из труб диаметром 40 мм, S1 = 72, S2 = 92. Средняя температура воздуха tЖ = 300°С, средняя скорость в узком сечении 10 м/с, угол атаки 60°.
Решение
При tЖ = 300°С, lЖ = 0,046 Вт/(м×К), n = 48,33×10-6 м2/с,
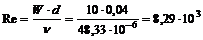 .
.
Режим течения турбулентный.
Уравнение подобия имеет вид:
 .
.
ey = 0,94 (по таблицам),  ,
,
 .
.
Отсюда среднее значение коэффициента теплоотдачи для труб третьего и последующих рядов:
 .
.
Для первого ряда:  .
.
Для второго ряда:  .
.

Задача 3
Гладкая плита, шириной 1 м и длиной 1,2 м, обдувается воздухом со скоростью 8 м/с. Определить средний коэффициент теплоотдачи, полный тепловой поток и изменение теплоотдачи вдоль поверхности, если температура стенки 60°С, а воздуха 20°С.
Решение
При tЖ = 20°С, lЖ = 0,0259 Вт/(м×К), n = 15,06×10-6 м2/с,
|
|
|
 .
.
Режим течения турбулентный.
 ,
,
 ,
,
 .
.
Для определения значений локального коэффициента теплоотдачи в качестве характерного размера примем координату х , которая изменяется от 0 до 1,2 м с шагом z = 0,1.
 . (2.1)
. (2.1)
Уравнения подобия
при Re < 5×105  ,
,
при Re ³ 5×105  .
.
Расчет значений a удобно провести на ЭВМ.
Задача 4
Определить потерю теплоты путем конвекции вертикальным неизолированным паропроводом диаметром 100 мм и высотой 4 м, если температура наружной стенки трубы 170°С, а температура среды (воздуха) 30°С.
Решение
При tЖ = 30°С, lЖ = 0,0267 Вт/(м×К), n = 16,0×10-6 м2/с, b = 3,4×10-3 1/К,
 ,
,
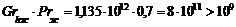 .
.
Следовательно, выбираем уравнение подобия вида:
 ,
,
 .
.
Искомая потеря теплоты:
 .
.
Дата добавления: 2018-02-15; просмотров: 2798; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
