Решение уравнений в символьном виде

Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:

· Если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр, поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении.

· Если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.

Чтобы решить уравнение символьно необходимо:

· Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш [Ctrl]=).

· Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью.

· Выбрать пункт менюСимволы→Переменные→Вычислить.

Нет необходимости приравнивать выражение нулю. Если MathCAD не находит знака равенства, он предполагает, что требуется приравнять выражение нулю.

Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:

· Напечатать ключевое слово Given.

· Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется [Ctrl]=.

· Напечатать функцию Find, соответствующую системе уравнений.

· Нажать [Ctrl].(клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства → .

· Щелкнуть мышью на функции Find.

Пример 6 иллюстрирует символьное решение системы уравнений в MathCAD.

Пример 6 Решение системы уравнений в символьном виде

Given

x + 2 ∙ π ∙ y = a

4 ∙ x+ y = b

– используйте [Ctrl]. (клавиша Ctrl. сопровождаемая точкой) для печати символьного знака равенства

Решение дифференциальных уравнений в MathCAD

Встроенные функции MathCAD предназначены для решения задачи Коши и граничных задач. Они решают их для нормальных систем обыкновенных дифференциальных уравнений.

Задачи для уравнений высших порядков сводятся к соответствующим задачам для нормальных систем.

Рассмотрим задачу Коши:

Численное решение этой задачи состоит в построении таблицы приближенных значений y_i,1 , y_i,2 , ..., y_i,N решения y₁ (x), y₂ (x), ..., y_N (x) на отрезке [x₀ , x_N ] в точках x₁ , x₂ , ..., x_N, которые называются узлами сетки.

Обозначив

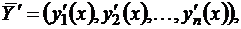
где – искомое решение, – вектор начальных условий, а 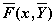–вектор правых частей, запишем систему дифференциальных уравнений в векторной форме:

В MathCAD решить задачу Коши для такой системы можно с помощью следующих функций:

· rkfixed(y, x1, x2, npoints, D) –решение задачи на отрезке методом Рунге—Кутты с постоянным шагом;

· Rkadapt(y, x1, x2, npoints, D) –решение задачи на отрезке методом Рунге—Кутты с автоматическим выбором шага;

· rkadapt(y, x1, x2, acc, npoints, D, kmax, save) –решения задачи в заданной точке методом Рунге-Кутты с автоматическим выбором шага;

Смысл параметров для всех функций одинаков и определяется математической постановкой задачи:
y– вектор начальных условий

x1, x2 – начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 – начальная точка, x2 – заданная точка;
npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку;
D– имя вектор-функции D(x,y) правых частей ,

; ( имя D – от Derivative – производная, имя вектора, содержащего выражения для производных (derivatives) искомого решения);
J – имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей:

acc – параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение не станет меньше save );

kmax – максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке, максимальное число строк в результате;

save – наименьшее допустимое значение шага неравномерной сетки. Результат работы функции – матрица, содержащая n+1; ее первый столбец содержит координаты узлов сетки, второй столбец – вычисленные приближенные значения решения y₁ (x) в узлах сетки,

(k+1) -й – значения решения y_k (x) в узлах сетки.

При решении задачи Коши для дифференциального уравнения первого порядка результат вычислений всех приведенных выше функций – матрица, в первом столбце которой содержатся координаты узлов сетки x₀ , x₁ , ..., x_N, а во втором – значения приближенного решения в соответствующих узлах (см. пример 8).

Для решения дифференциального уравнения более высокого порядка используют функцию Odesolve (пример 7).

Решение системы дифференциальных уравнений рассмотрено в прил. 2.

Пример 7

Будем решать граничную задачу y''-sin(x)y'+y = x/2p, y(0)=0, y'(4 p )=1 с помощью функции Odesolve. Прежде чем вводить дифференциальное уравнение, введем ключевое слово Given, а затем – дифференциальное уравнение. При вводе дифференциального уравнения необходимо в скобках указать аргумент искомого решения и использовать знак символьного равенства.

Следом за уравнением необходимо ввести граничные условия. При вводе граничных условий, как и при вводе уравнения, следует использовать знак символьного равенства. Знак символьного равенства можно ввести щелчком по соответствующей кнопке в панели Evaluation, а также ввести с клавиатуры, нажав одновременно клавиши <Ctrl> и <=>. Выполняем

В результате переменной y присваиваются значения численного решения задачи Коши на отрезке (0, 4π)

Построим график найденного решения y(x) (рис. 3).

Для того чтобы построить график решения y(x), щелкните в панели Graph по пиктограмме декартова графика, введите в помеченных позициях имена аргумента и функции и щелкните по свободному месту в рабочем документе вне выделяющей рамки

Пример 8

Будем решать на отрезке [0, 3] с помощью функции rkfixed на равномерной сетке из 30 узлов задачу Коши для системы уравнений:

y₁′ = – y₂+sin(x*y₃)

y₂′ = – y₁²

y₃′ = – y₃– y₁

Начальные условия: y₁(0) = 1, y₂(0) = 0, y₃(0) = 1.

Прежде чем вводить дифференциальное уравнение, определим номер первой компоненты вектора цифрой 1 (а не нулем, как предполагается по умолчанию)

Ключевое слово ORIGIN обязательно писать з а г л а в н ы м и буквами.

Полагая, что решение – это вектор y с тремя компонентами , введем начальное условие.. Для того чтобы определить матрицу, введите ее имя и знак присваивания, а затем щелкните по символу матрицы в панели Matrix и введите размеры матрицы – число строк и число столбцов. В итоге получим: x:=0..3 ORIGIN:=1

Определим правую часть уравнения – матрицу D(x,y) , которая в данном случае является вектором с тремя компонентами (по числу уравнений в системе). Здесь x – независимая переменная, y – с компонентами y1 и y2 и y3.

Затем вводим

В результате матрица Y содержит решение: в первом ее столбце значения x, а во втором и последующих столбцах – соответствующие значения полученного решения.

Для того чтобы вывести в рабочий документ матрицу Y, введите с клавиатуры имя матрицы Y и знак равенства.

Для того чтобы построить график решения y(x) (рис. 4), щелкните в панели Graph по пиктограмме декартова графика, введите в помеченных позициях имена аргумента (первый столбец матрицы Y) и функции (второй столбец матрицы Y) и щелкните по свободному месту в рабочем документе вне выделяющей рамки. Для того чтобы ввести имя столбца матрицы Y, введите имя матрицы, затем щелкните по символу номера столбца в панели Matrix (там он обозначен М^{[ ]})и введите номер столбца в помеченной позиции в угловых скобках.

Приложение 2.

Дата добавления: 2018-02-15; просмотров: 1255; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 15 161718 19 20 Следующая ⇒

Мы поможем в написании ваших работ!