ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

⇐ ПредыдущаяСтр 14 из 20Следующая ⇒

П р и м е р 7.1. В электрическом поле точечного заряда напряжение между точками а и b равно 25 В (рис. 7.1). Определить значение и направление напряженности поля в точке с, если точки a, b и с лежат в плоскости рисунка.

Р е ш е н и е.Напряженность электрического поля точечного заряда в произвольной точке

E = . (1)

Напряженность электрического поля в точке с

E_с= . (2)

Напряжение между точками a и b

= (3)

Получив выражение для заряда q из уравнения (3) и подставив его в уравнение (2), найдем

Е_с= = 525 В.

П р и м е р 7.2. Коаксиальный кабель имеет радиусы внутренней жилы a = 2 мм и внешней оболочки b = 5 мм.

Определить емкость кабеля на единицу длины и под какое напряжение можно подключить кабель, если максимальная напряженность поля не должна превышать 1/3 пробивной напряженности, равной Е_пр = 2·10⁴кВ/м.

Р е ш е н и е.Проведем вокруг внутренней жилы коаксиального кабеля цилиндрическую поверхность радиусом r и длиной l.

По теореме Гаусса ∫ .

Из условий симметрии находим, что напряженность электрического поля Е направлена по радиусу и на торцевых поверхностях

Тогда уравнение Гаусса можно записать в виде Е·2πrl = q/ε_a.

Откуда E = q/2πε_arl = , где τ -линейная плотность заряда.

По определению потенциал в любой точке равен

Полагая потенциал равным нулю на поверхности коаксиального кабеля при r = b, найдем произвольную постоянную const = .

Тогда потенциал в любой точке равен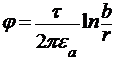

Потенциал внутренней жилы коаксиального кабеля (при r = a) определим по уравнению .

Это позволяет выразить линейную плотность заряда через напряжение U

и определить емкость кабеля на единицу длины

Напряженность электрического поля в любой точке

Напряженность поля максимальна на поверхности внутреннего цилиндра, т.е. в точках r = a: Е_max= . (1)

По условию Е_max=Е_пр/3. (2)

Решая уравнение (1) относительно выражения U и учитывая соотношение (2), получаем = 12,2 кВ.

П р и м е р 7.3.Определить потенциал точки М, расположенной между двумя заряженными осями. Определить положение эквипотенциалей.

Р е ш е н и е .Пусть одна ось на единицу длины имеет заряд +τ, другая – заряд – τ. Возьмем в поле некоторую произвольную точку М (рис.7.3) Результирующая напряженность поля в ней равна геометрической сумме напряженностей от обоих зарядов. Расстояние точки М до положительно заряженной оси обозначим через а, до отрицательно заряженной оси – через b. Потенциал есть функция скалярная. Потенциал точки М равен сумме потенциалов от каждой оси: .

Потенциал определяется с точностью до постоянной С. Зададим φ = 0 при a = b. Для этого проведем ось х декартовой системы координат через заряженные оси, а ось y посредине между заряженными осями. Тогда при расположении точки М на оси у (при х = 0) всегда а = b и

φ_М = С = 0. В остальных случаях

Эквипотенциаль представляет собой совокупность точек, отношение расстояний которых до двух заданных точек есть величина постоянная, т.е. b/a = const = k . Поскольку

и то ,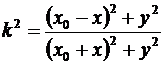

или .

Последнее уравнение определяет окружность радиуса ,

у которой центр смещен относительно начала координат на расстояние 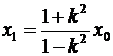. Между величинами x₁, R, x₀ выполняется равенство x₁² = x₀²+R²

Таким образом, уравнение эквипотенциали для двух заряженных осей является окружность, смещенная относительно начала координат. Для построения картины поля нужно, чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, т.е.

или при возрастании порядкового номера эквипотенциали числа k должны изменяться по геометрической прогрессии .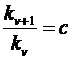

П р и м е р 7.4.Два провода радиусом 1 мм расположены на расстоянии 10 мм друг от друга. Провода находятся под напряжением 100 В. Построить картину электростатического поля между проводами. Рассчитать емкость на единицу длины. Разбить весь поток на 12 трубок равного потока, эквипотенциали провести через 10 В.

Р е ш е н и е. Известно, что поверхность проводящего тела является поверхностью с равным потенциалом (эквипотенциальной поверхностью) и напряженность электрического поля внутри проводника равна нулю.

Так как провода находятся под напряжением 100 В, то можно положить, что потенциал левого проводника равен 50 В, а у правого проводника – 50 В (потенциал определяется с точностью до произвольной постоянной). При таком условии поверхность с потенциалом равном нулю будет находиться посередине между проводниками.

Из предыдущей задачи известно, что эквипотенциали для двух заряженных осей являются окружностями, смещенными на разные расстояния по отношению к началу координат. В рассматриваемой задаче поверхности проводников являются эквипотенциалями и имеют вид окружности. По-видимому можно найти такое положение заряженных осей, чтобы они создавали эквипотенциаль радиусом

1 мм с потенциалом 50 В, и тогда все расчеты можно провести, используя формулы предыдущей задачи.

Полагая радиус эквипотенциали R = 1 мм, координату центра эквипотенциали (смещение от начала координат) x₁ = l/2 = 5 мм, найдем координату заряженной оси .

Возьмем точку М на эквипотенциале (для удобства вычисления расположим ее при y = 0) и найдем отношение расстояний от точки М до заряженных осей (рис. 7.4)

Используя полученное в предыдущем примере уравнение для потенциала

и подставляя в него значение потенциала точки М и величину отношения а/b = k_м = 0,101, найдем линейную плотность заряда

**)

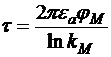Для определения положения эквипотенциалей со значениями

φ₁₀ = – 10 В, φ₂₀ = –20 В, φ₃₀ = –30 В, φ₄₀ = –40 В используем уравнение (*) и находим величины k₁₀, k₂₀, k₃₀, k₄₀:

Аналогично

Используя полученные ранее уравнения для радиуса и координаты центра эквипотенциалей найдем соответствующие величины. Например, для эквипотенциали φ₃₀ = –30 В находим

= 5,57 мм.

Откладывая от начала координат величину x₃₀ = 5,57 мм, находим координату центра окружности и радиусом R₃₀= =2,65 мм проводим дугу (рис.7.4). Во всех точках, лежащих на этой дуге потенциал равен φ₃₀ = –30 В. Аналогично строим эквипотенциали φ_10,φ₂₀ и φ₄₀ (рис.7.5). Эквипотенциали с положительными значениями потенциала 10, 20, 30, 40 В строят по тем же цифрам, но откладывают их слева от оси y.

Для определения емкости на единицу длины используем уравнение (**):

Для построения силовых линий электростатического поля двух заряженных осей используем уравнение любой линии напряженности поля

Эта линия представляет собой дугу окружности, проходящей через заряженные оси. Действительно для всех точек, лежащих на дуге

V = const угол θ = θ₂ – θ₁ будет неизменным, так как он измеряется половиной дуги AFB (рис.7.6).

При этом центральный угол AOF тоже равен θ, так как он определяется дугой ASF, которая равна половине дуги AFB. Это позволяет определить радиус этой дуги и смещение ее центра у₁ = OO₁ = x₀ ctgβ, где β = π – θ.

Чтобы подразделить поле на трубки равного потока следует получить разности ∆V = V_ν₊₁– V_ν одинаковые для двух любых соседних линий. Для этого необходимо при переходе от любой линии напряженности поля к соседней, изменять угол θ на постоянную величину ∆θ. Чтобы разбить весь поток электростатического поля на 12 трубок равного потока, нужно дать приращения углов θ на , т.е. иметь углы θ равные . При этом шесть трубок будет выше оси x и шесть трубок – ниже. Для проведения соответствующих окружностей находим координаты их центров по уравнению y_к = x₀ctgθ_к. Получаем у₁ = ±9,9мм, у₂ = ± 5,8 мм, у₃ = 4,9 мм. Окружности должны были проходить через заряженные оси, так как в данной задаче рассматривается поле, созданное двумя проводниками и внутри проводников электрическое поле отсутствует, то силовые линии, ограничивающие трубки равного потока должны начинаться на левом проводнике и заканчиваться на правом (рис.7.5).

По картине поля можно ориентировочно определить емкость двухпроводной линии на единицу длины. Полагая, что при пересечении силовых линий и эквипотенциалей на рис.7.5 получились криволинейные квадраты, найдем

где m – число трубок равного потока, n – число приращений потенциала. Сравнивая полученный результат с вычисленным ранее, находим, что погрешность графического метода порядка 12 %.

П р и м е р 7.5. Рассчитать и построить картину поля коаксиального кабеля со смещенной жилой, если радиус жилы R₁ = 1 мм, радиус внутренней поверхности экрана R₂ = 4 мм, а смещение осей

d = 0,5мм. Кабель находится под напряжением 100 В. Определить емкость кабеля на единицу длины.

Р е ш е н и е. Так как металлические поверхности жилы и экрана являются эквипотенциальными и в поперечном сечении представляют окружности, то используя аналогию с эквипотенциальными поверхностями двух заряженных осей (рис. 7.7), рассчитаем линейную плотность заряда, которая создала бы разность потенциалов 100 В между эквипотенциалями диаметрами 1 и 4 мм. При этом поверхность с потенциалом, равным нулю, окажется в стороне, потенциалы точек N и M будут сравнительно большими, но разность их будет равна 100 В, т.е. φ_N – φ_M = 100 В.

Обозначая величины смещения центров окружностей от начала координат (где φ = 0) соответственно х₁ и х₂, запишем для них уравнение

Решая полученную систему уравнений, находим

Потенциалы точек М и N определяются уравнениями

где

Зная разность потенциалов φ_N – φ_M = 100 В, определим линейную плотность заряда, обеспечивающую эту разность потенциалов:

или

Тогда потенциал точки М равен

Для построения эквипотенциалей внутри коаксиального кабеля нужно сначала найти значение коэффициентов k₂₀, k₄₀, k₆₀, k₈₀. Например, для эквипотенциали, соответствующей 40 % напряжения, приложенного между электродами, найдем k₄₀ из уравнения:

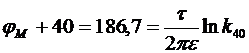или

Тогда радиус эквипотенциали и координата ее центра определяем по уравнению

, .

Аналогично определяем

и соответствующие радиусы эквипотенциалей и координаты их центров.

Емкость на единицу длины коаксиального кабеля со смещенной жилой определяем по формуле

Ф/м.

П р и м е р 7.6. Вдоль двухпроводной линии протекает постоянный ток I = 36 А. Направление тока в проводах линии показательно на рис. 7.8. Расстояние между осями проводов d = 1 м.

Определить разность скалярных магнитных потенциалов между точками M и N, M и P, т.е. и . Координаты точек x_M = 0,5м; y_M = 0,5м; x_N = 0; y_N = 0,5м; x_р= – 0,5м;

y_р= – 0,5м. Качественно построить картину магнитного поля двухпроводной линии.

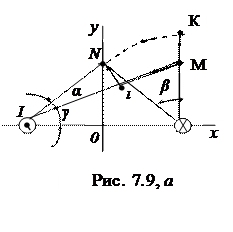Р е ш е н и е. Магнитное напряжение между точками M и N по пути MlN, обусловленное током левого провода

(рис. 7.9,а), U_mM= .

Магнитное напряжение между точками M и N по пути MКN, обусловленное током правого провода,

, где β = 45º,

так как . Для определения угла α сначала найдем угол γ, считая tg γ = y_м/d = 0,5; γ =26,5º, и α = 45º – 26,5º = 18,5º.

Магнитное напряжение между точками M и N

U_mMN = = 36/360º (– 45º+18,5º) = – 2,65 А.

Магнитное напряжение между точками M и P (рис. 7.9, б)

U_mMP= = (I/360) β₁ – (I/360) α₁= 12,5 А,

где β₁= 360º – 90º – 26,5º = 243,5º; α₁= 90º+26,5º = 116,5º.

Картина магнитного поля двухпроводной линии приведена на рис. 7.9, в.

П р и м е р 7.7. Вдоль длинного цилиндрического стального провода протекает постоянный ток. Радиус провода r₀ =1 см. Относительная магнитная проницаемость стали μ = 50. Средой, окружающей провод, является воздух. Проекция векторного магнитного потенциала на ось z меняется в функции расстояний от оси провода по закону A₁= – 6,28 r²Вб/м, а вне провода она меняется по закону

А₂= – 25,1· 10^{-6 In} – 6,28·10^-4Вб/м.

Найти законы изменения модуля напряженности магнитного поля и модуля вектора намагниченности в функции расстояния от оси провода. Построить графики Н = f ( R ) и J = f₁ ( R ) при 0 < r < ∞.

Р е ш е н и е.Так как , то модуль вектора магнитной индукции внутри и вне провода найдем из выражений

B₁= B₁_α = rot_α = – = 12,56 r,

B₂= B₂_α = rot_α = – = 25,1·10^-6 1/r.

Определим модуль напряженности магнитного поля внутри и вне провода, полагая μ_1а = μ∙μ₀, μ_2а = μ₀:

Н₁=В₁/μ_1а=2·10⁵r А/м, (1)

Н₂=В₂/μ_2а=20 1/ r А/м. (2)

Пользуясь выражениями (1) и (2), строим график зависимости Н =f(r) (рис. 7.10). Так как индукция , то модуль вектора

намагниченности внутри провода

J₁= В₁/μ₀– H₁=9,8·10⁶r А/м; (3)

модуль вектора намагниченности вне провода J₂= 0. (4)

По уравнениям (3) и (4) строим график зависимости J= f(r) (рис.7.10).

П р и м е р 7.8. Определить индуктивность двухпроводной линии, если радиус проводников а, а расстояние между проводниками d. (Рис.7.11)

Р е ш е н и е. Выберем внутри проводника площадку dS = ldr и определим магнитный поток внутри проводника

;

и потокосцепление

. (1)

Так как через сечение проводника радиуса r протекает часть тока I, равная ,

то из закона полного тока Hdl=i определим

и подставим это выражение в уравнение (1):

μ_a ldr =

Определим магнитный поток и потокосцепление между проводниками от одного проводника (снаружи)

Определим суммарное потокосцепление от двух проводников

Индуктивность двухпроводной линии

При d >>a и немагнитных проводниках .

П р и м е р 7.9. Электрический ток i = 100 А течет по бесконечно длинному прямолинейному проводу круглого сечения радиусом R = 2 см, расположенному в однородной среде с магнитной проницаемостью μ₀. Рассчитайте и постройте зависимости А(r), В(r) внутри и вне провода.

Р е ш е н и е. Векторный магнитный потенциал удовлетворяет внутри и вне провода уравнениям при 0 ≤ r ≤ R;

при r ≥ R, решение этих уравнений имеет вид

при 0 ≤ r ≤ R

и A(r) = C₃ ln r + C₄, B(r) = – C₃/r при r ≥ R.

Для нахождения входящих в решения постоянных С₁, С₂, С₃, С₄ используем следующие условия. Так как при r = 0 имеем В = 0, то

C₁ = 0. При r = R магнитная индукция не может иметь разрыв, что приводит к условию откуда получаем .

Потенциал А при r = R также непрерывен:

Одна из постоянных (С₂ или С₄) может иметь произвольное конечное значение, так как изменение векторного магнитного потенциала на постоянную не оказывает влияния на магнитную индукцию. Принимая С₄ = 0, получаем С₂ = –μ₀i (lnR – 0,5)/2π и окончательно можем написать

при 0 ≤ r ≤ R;

при r ≥ R.

П р и м е р 7.10. Используя метод наложения, рассчитайте зависимость А(х) вдоль линии, соединяющей ближайшие друг к другу точки двух бесконечно длинных прямолинейных проводов круглого сечения с токами встречных направлений, расположенных в однородной среде с магнитной проницаемостью μ₀. Расстояние между осями проводов d = 10 см. Ток каждого провода i = 80 А.

Р е ш е н и е. Поместим начало прямоугольной системы координат в точке на расстоянии 0,5d от осей проводов (рис.7.12.). Потенциал вне проводов в точках оси х,в соответствии с решением предыдущего примера равен

Постоянную С принимаем равной нулю, так как при x = 0 имеем А = 0

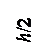
П р и м е р 7.11. В пазу прямоугольной формы, изображенном на рис.7.13, размещены два провода прямоугольного сечения с токами встречных направлений. Допуская, что имеющий единственную составляющую А_z векторный магнитный потенциал зависит только от координаты у, найдите зависимости А_z(у), В_х(у) для 0 ≤ у ≤ h и постройте кривые их изменения. Ток одного провода i = 50 А, магнитная проницаемость вещества провода μ₀.

Р е ш е н и е. Векторный магнитный

потенциал удовлетворяет уравнению

где

Интегрируя уравнение, получаем

при 0 ≤ y ≤ 0,5h и

при 0,5h ≤ y ≤ h

Постоянную С₁ интегрирования определяем из условия B_x = 0 при y = 0: получаем C₁ = 0. Интегрирование функции B_x(y) = dA/dy приводит к выражениям при 0 ≤ y ≤ 0,5h и

при 0,5h ≤ y ≤ h.

Постоянную С можно принять произвольной, например, равной нулю, поскольку ее значение не оказывает влияния на магнитную индукцию. Кривые зависимостей В_х(у), А(у) (принято С = 0) показаны на рис.7.14.

П р и м е р 7.12.Постройте картину магнитного поля в воздушной области, ограниченной внутренним контуром стальных листов (рис 7.15), принимая допущение о том, что магнитная проницаемость вещества сердечника бесконечно велика и что магнитное поле является плоскопараллельным, не изменяющимся в направлении, перпендикулярном плоскости листов. Обмотку центрального стержня представьте в виде бесконечно тонкого охватывающего стержень слоя тока, по высоте которого ток распределен равномерно. Рассчитайте индуктивность L обмотки ,используя построенную картину магнитного поля.

Обозначения размеров магнитной системы показаны на рис.7.15:

а = с = 12 см, е = 2см, b = 6 см , d = 4 см , h = 6 см. Число витков обмотки w = 100, ток в обмотке I = 1 A.

Р е ш е н и е.Учитывая симметрию поля относительно пунктирной линии (см.рис.7.15), ограничимся построением картины поля лишь в половине всей области. Для построения картины магнитного поля, включающей линии напряженности и линии постоянных значений скалярного магнитного потенциала, следует задать граничные условия для скалярного магнитного потенциала на линии ABCDEFGA. Поскольку обмотка стержня представлена в виде бесконечно тонкого слоя с постоянной линейной плотностью тока, то скалярный магнитный потенциал изменяется вдоль линии CD по линейному закону, причем разность потенциалов между точками С и D равна Iw = 100 А. Потенциал в точке D задаем равным нулю. Так как магнитная проницаемость материала сердечника принята бесконечно большой, то скалярный потенциал на линии DEFG сохраняется постоянным и равным нулю. По той же причине потенциал будет постоянным и равным 100 А на линии ABC. Линия AG является линией симметрии; нормальная к ней составляющая напряженности Н_n магнитного поля равна нулю, и поэтому на ней

При построении картины поля следует соблюдать следующие правила: а) линии напряженности поля и линии постоянного потенциала должны пересекаться под прямым углом, б) линии напряженности поля должны подходить под прямым углом к поверхностям, на которых потенциал постоянный, в) ячейки сетки, образованные линиями напряженности поля и линиями постоянного потенциала, должны быть подобными.

Примем изменение ΔU_m потенциала при переходе от любой линии к соседней равным 25 А. В этом случае следует изобразить всего три линии, на которых потенциал равен 25 , 50 и 75 А. Необходимо отметить точки токового слоя (p, q, r), в которых потенциал принимает эти значения, и проводить линии, начиная с этих точек. Так как линейная плотность тока постоянна, то эти точки распределены вдоль линии CD равномерно. Определив ориентировочно вид этих линий, переходим к изображению линий напряженности магнитного поля, стараясь выполнить правила построения картины поля. Обычно линии напряженности поля проводят так, чтобы ячейки были квадратными или близкими к ним, т.е. чтобы отношение Δa/Δn (рис.7.16) было близким к единице.

После этого следует скорректировать положение линий постоянного потенциала, затем – положение линий напряженности поля и т. д. Эту процедуру следует выполнять до тех пор, пока картина поля не будет удовлетворять требуемым правилам. В итоге получаем картину

поля (рис.7.16), в которой линии напряженности подразделяют всю область на трубки постоянных значений потока. Заметим, что линии напряженности поля подходят к линии CD под углом, не равным 90°, так как на этой линии распределен слой тока.

Для расчета индуктивности L, находим магнитный поток, сцепленный с обмоткой среднего стержня. С этой целью вычисляем магнитный поток одной трубки, а также число трубок, сцепленных с обмоткой. Магнитный поток трубки равен ΔФ = μ₀HΔS= μ₀ (ΔU_m/Δn ) Δаt = 8π·10^-7Вб (принято толщина сердечника t = 0,02м Δa/Δn = 1). Трубки магнитного потока с номерами 1, 2,... 6 (рис.7.16) охватывают всю обмотку, тогда как трубки с номерами 7, 8, 9 охватывает лишь ее части. Пунктирными линиями на рис.7.16 изображены средние, или осевые линии некоторых трубок, по положению которых и определяем, какую часть обмотки охватывает трубка потока.

Таким образом, полный поток, сцепленный с обмоткой среднего стержня, составляет ψ₁ = 2ΔФw₁(m₀ + h₁/h + h₂/h ... ), где m₀ – число трубок, сцепленных со всеми витками w₁обмотки. Число слагаемых вида h_K/h равно числу трубок, сцепленных не со всей обмоткой. Имеем

ψ₁ = 1,6π·10^-6(6 +0,97 + 0,84+0,67) ≈ 4,3·10^-5Вб, L = ψ₁/i = 4,3·10^-5Гн.

П р и м е р 7.13. Плоская электромагнитная волна проникает из воздуха в металлическую плиту. Удельная проводимость металла

γ = 5·10⁶ См/м, его относительная магнитная проницаемость μ = 1. Фронт волны параллелен поверхности плиты. Частота колебаний f = =5000 Гц. Амплитуда плотности тока на поверхности J_m= =5√2·10⁵ А/м².

Определить активную мощность, поглощаемую слоем металла толщиной 0,5 см и площадью 1м². Найти глубину проникновения электромагнитной волны h и ее длину λ в металле.

Р е ш е н и е. Комплекс действующего значения модуля вектора Пойнтинга на поверхности плиты ,

где ; ; Z_B = = 8,85·10^-5е^j^45º Ом.

Подставляя числовые значения в последние уравнения, получим

=1130 е^j^45ºВт/м².

Комплекс действующего значения модуля вектора Пойтинга на глубине x = 0,5 см

= 1130 е ^{– 314 · 0,005}е^j^45º= 235 е^j^45ºВт /м²,

где κ = = 314 м ^-1.

Активная мощность, поглощаемая слоем металла толщиной

5 мм и площадью s = 1 м², P = (S₁-S₂)s cos 45º = 632 Вт.

Глубина проникновения электромагнитной волны в металл

h=1/κ=3,18·10^{-3 м.}

Длина волны λ = 2π/ κ = 2·10^{-2 м.}

П р и м е р 7.14. Стальная полоса с поперечными размерами

2а = 1 мм и h = 50 мм находится в переменном магнитном поле, изменяющемся во времени по синусоидальному закону с частотой f = 500 Гц

(рис. 7.17) Вектор напряженности магнитного поля на поверхности шины А/м. Удельная проводимость стали γ = 4·10⁶См/м, относительная магнитная проницаемость μ = 200.

Найти действующее значение магнитного потока, проходящего через поперечное сечение шины. Построить график зависимости модуля действующего значения плотности вихревых токов от координаты z.

Р е ш е н и е.Определив м^-1, найдем и среднее значение магнитной индукциипо сечению шины = 5,06·10^-3е^j^31º Tл,

где th pa = =0,895 е^j^31º.

Действующее значение магнитного потока

=25,3 ·10^-8Вб.

Плотность вихревых токов распределяется по сечению шины по закону

·.

Подставим численные значения в последнее выражение:

при z = 0,25мм J = 1,44∙10⁴ А/м²,

z = 0,5мм J = 3,18∙10⁴ А/м² .

По этим данным строим зависимость модуля действующих значений плотности вихревых токов в функции координаты z, (рис. 7.18).

П р и м е р 7.15. Определить активное и внутреннее индуктивное сопротивление медной прямоугольной шины длиной 1 м, толщиной 1 мм и высотой 20 мм для переменного тока частотой

ω = 10⁵ рад/с, если См/м, μ_r = 1.

Р е ш е н и е. Используя теорему Пойнтинга в комплексной форме и полученные ранее уравнения для напряженностей электрического и магнитного полей

где h – высота, 2a – толщина пластины, р – корень характеристического уравнения. Найдем комплексное сопротивление шины

При этом учитываем взаимную перпендикулярность векторов E и H и направленность потока вектора Пойнтинга внутрь пластины через две боковые поверхности величиной 2hl.

Определяем значения корня характеристического уравнения

Вычисляем величину

полагая p = k + jk;

, , .

Подставляем вычисленные значения и определяем комплексное сопротивление шины на единицу длины

Ом/м

Таким образом, активное сопротивление шины длиной 1 м равно Ом, а индуктивное сопротивление равно Ом.

П р и м е р 7.16. Определить активное и полное индуктивное сопротивление двух медных шин длиной 1 м, высотой 20 мм и толщиной 1 мм, расположенных на расстоянии b = 2 мм, если по ним проходит ток частотой ω = 10⁵ рад/с.

Р е ш е н и е. Полное сопротивление двух шин будет складываться из внутреннего комплексного сопротивления шин и индуктивного сопротивления, обусловленного магнитным потоком, проходящим в пространстве между шинами Z_полн= 2Z_вн+2jX_сн

Учитывая эффект близости и полученные ранее формулы для напряженностей электрического и магнитного полей

Определяем внутреннее комплексное сопротивление одной шины

где

Отметим, что из-за эффекта близости активное сопротивление шины возросло (см предыдущий пример) с 9,8∙10^-4 до 15,7∙10^-4 Ом/м.

Определяем индуктивное сопротивление, обусловленное магнитным потоком, проходящим в пространстве между шинами:

Полное сопротивление линии из двух шин длиной 1 м равно

Ом.

З а д а ч и

1. Определить частоты f , при которых землю можно считать «практически» диэлектриком. Удельная проводимость земли γ, абсолютная диэлектрическая проницаемость ε_а.

Указание. На практике считают диэлектриком среду, для которой отношение плотности тока проводимости к плотности тока смещения

1. f < 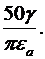2. f > 3. f > 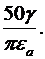4. f <

2. В проводящей среде с удельной проводимостью γ = 57∙10⁶ См/м и абсолютной магнитной проницаемостью μ₀ распространяется плоская электромагнитная волна. Определить ее фазовую скорость v и длину волны λ при частоте f = 10⁶ Гц.

5.v = 0,418 м/с; λ = 4,18 см. 6.v = 418 м/с; λ =0,418 см.

7.v = 300 м/с; λ = 418 см. 8.v = 4,18 м/с; λ =0,0418 см.

3.Две параллельные разноименно заряженные оси расположены

в воздухе на расстоянии D = 100 см друг от друга . Линейная плотность заряда осей

τ = 100 пКл/см. Определить координату х₀ центра эквипотенциальной линии с потенциалом φ = – 249 В.

9. x₀ = 51,3 см. 10. x₀ = 56,7 см.

11. x₀ = 61,8 см 12. x₀ = 71,5 см.

4.Определить погонную емкость С₀ между двумя весьма длинными проводящими цилиндрами кругового сечения с параллельными осями. Радиусы цилиндров r = 15 см, расстояние между геометрическими осями D=50 см, диэлектрическая проницаемость среды ε =1.

13. C₀=46,4 пФ/м. 14. C₀=13,2 пФ/м.

15. C₀=25,4 пФ/м. 16. C₀=50,8 пФ/м.

5. Через заземлитель в виде полусферы пропускают постоянный ток I. Вольтметр, присоединенный к двум зондам, отстоящим на расстоянии a и b от центра полусферы, показывает напряжение U. Определить удельную проводимость γ почвы.

17. 18.

19. 20.

ОТВЕТЫ

Глава1

1) I₁=40 A; I₃=40/3 A; I₅=80/3 A; I₄=80/9 A; I₁=160/9 A; 2) 9 A; 3) 1 Oм; 4) 2R; 5) 200 B; 6) I_H=10 A; I_E=5 A; P=500 Bт; 7) I₁=20 A; I₂= =I₃=25 A; 8) 2 A; 9) 1; 10) 2; 11) 190 A; 12) 162 Вт; 13) 400 A; 14) I₁=0,667(1+I₂) A; 15) U=25-0,5I B;16) R_i=25 Oм; R; R_ш=0,025 Ом; 17) нельзя; 18) а)8 А; 80 В; б) 6 А; 60 В; в) 4,8 А; 48 В; г) 4 А; 40 В.

Глава 2

1)P=15 Вт, cosj=0,6; 2)U_ab =100 В; 3) 3,46 А; 4) φ = 15⁰ R = 4,83 Ом, X =1,3 Ом; 5) ,Z_э= Z₂; 6) 630 В; 7) I=0,0216 А, U_R=2,6 В, U_c=3,9 В, U_L=15,6 В; 8) I₁=0,5+j0,5 А; I₂= –0,5+j0,5 А; 9) Ом; Ом; Ом; 10) w=433c^-1; 11) А; А; А; А; 12) а) U₂=80 В; P₁=0; б)P₂=130 Вт; U₂=27 В; 13) Ф; 14) R=4 Ом; L=0,1 Гн; 15) в.