УРАВНЕНИЯ ИЗОБАРЫ И ИЗОХОРЫ ХИМИЧЕСКОЙ РЕАКЦИИ.
РАСЧЕТ КОНСТАНТ РАВНОВЕСИЯ И ТЕПЛОВЫХ ЭФФЕКТОВ ХИМИЧЕСКИХ РЕАКЦИЙ ПО УРАВНЕНИЮ ИЗОБАРЫ
Количественно влияние температуры на химическое равновесие описывается уравнением изобары химической реакции.
Рассмотрим вывод уравнения изобары:
Перепишем уравнения изотермы в следующем виде:

Продифференцируем это уравнение по температуре и перепишем его:

выражение в квадратных скобках есть  , тогда:
, тогда:

Представим уравнение Гиббса – Гельмгольца в виде:

Левые части последних уравнений равны, следовательно, равны и правые:

Получаем:  (3.2.1)
(3.2.1)
(3.2.1) – уравнение изобары химической реакции в дифференциальной форме.
 (3.2.2)
(3.2.2)
(3.2.2) – уравнение изохоры химической реакции в дифференциальной форме.
Из этих уравнений следует, что влияние температуры на константу равновесия определяется знаком теплового эффекта. Если реакция эндотермическая, т.е.


и с повышением температуры константа равновесия будет расти, равновесие будет смещаться в сторону продуктов реакции. Если реакция экзотермическая, т.е.

то с повышением температуры константа равновесия будет уменьшаться, равновесие будет смещаться в сторону реагентов.
При помощи уравнений изобары и изохоры можно не только определить изменение констант равновесия в зависимости от температуры, но и найти тепловой эффект химической реакции. Для этого получим уравнение изобары в интегральной форме.
|
|
|
Разделим переменные:

Интегрирование проведем для двух случаев.
1) Первый: DН = const. Тогда после интегрирования имеем:
 (3.2.3)
(3.2.3)
где В – постоянная интегрирования.
Согласно уравнению (3.2.3) можно рассчитать тепловой эффект реакции графическим методом, что представлено на рис. 3.2.1.
Из рис. 3.2.1. видно, что  Þ DН = – Rtga
Þ DН = – Rtga
 |
Рис. 3.2.1. Графическое определение теплового эффекта
Интегрирование можно провести в интервале температур:


 Þ
Þ 
2) Второй: DН ≠ const. В этом случае интегрирование проводят с использованием уравнения Кирхгофа.
Зависимость Кх от давления может быть определена следующим образом:

Kp и Kc от давления не зависят, а Kx является функцией давления:
 (3.2.4)
(3.2.4)
Уравнение (3.2.4) называется уравнением Планка-Ван-Лаара, согласно которому при повышении давления равновесие смещается в сторону меньшего объема.
ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ
ТЕМПЕРАТУРЫ. МЕТОД ШВАРЦМАНА-ТЕМКИНА
|
|
|
В основе метода расчета, основанного на использовании стандартных термодинамических величин, используются два уравнения:


|


1. Тепловой эффект реакции при температуре Т и Р = const можно вычислить по уравнению Кирхгофа в интегральной форме:
 (3.3.2)
(3.3.2)
Величину  находят с помощью таблиц стандартных теплот образования участников реакции
находят с помощью таблиц стандартных теплот образования участников реакции
|
 (3.3.3)
(3.3.3)
2. Для расчета энтропии используют уравнение:
 , (3.3.4)
, (3.3.4)
которое при стандартных условиях принимает следующий вид:
 (3.3.5)
(3.3.5)
Проинтегрируем это уравнение в интервале температур от 298 К до Т и получим:
 (3.3.6)
(3.3.6)
Величину  находят с помощью таблиц стандартных энтропий
находят с помощью таблиц стандартных энтропий
|
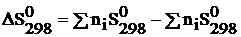 (3.3.7)
(3.3.7)
DСр определяется с помощью справочных таблиц как функция температуры Ср = f(T). Известно, что в общем случае для неорганических и органических соединений эта зависимость выражается следующим рядом:
|
|
|
DСр = Dа + DвТ + DСТ2 + DС/Т –2 + …, (3.3.8)
|
Объединяя все выражения, получим:
 (3.3.9)
(3.3.9)
и подставим в выражение для константы равновесия:
 (3.3.10)
(3.3.10)
Вычисление двух последних интегралов является довольно кропотливой операцией и на практике пользуются методом, предложенным Темкиным и Шварцманом. Суть метода заключается в том, что значение DСр = f(T) подставляют в подинтегральное выражение двух последних интегралов и вычисляют их.



 (3.3.11)
(3.3.11)
Объединяя члены, содержащие Dа, Dв и т.д. и приводя подобные, получим:

 (3.3.12)
(3.3.12)
Обозначим величины в квадратных скобках Dа, Dв, Dс и Dс¢ соответственно через М0, М1, М2, М–2.Индекс при коэффициенте М равен показателю степени, в которой входит температура в уравнении с = f(T). Таким образом,

 (3.3.13)
(3.3.13)
В структуре М1, М2, М–2 можно легко усмотреть общую закономерность и записать общую формулу для расчета всех коэффициентов, включая М3, отвечающей опущенному ранее в выражении
|
|
|
DСр = f(T) cT3.
 ,
,
где n = 1, 2, 3 или (-2).
Коэффициенты M0, Mn являются функциями только температуры. Их значения вычислены для различных температур, обычно с интервалом 500 или 1000, и сведены в таблицы.
Переходя к десятичным логарифмам, получим окончательное уравнение для вычисления константы равновесия Кр по методу Темкина – Шварцмана:
 (3.3.14)
(3.3.14)
Если  и
и  и теплоемкость выражены в джоулях, то 2,303 . R = 19,14 Дж/моль . град, а если в калориях, то 4,576 кал/ моль . град.
и теплоемкость выражены в джоулях, то 2,303 . R = 19,14 Дж/моль . град, а если в калориях, то 4,576 кал/ моль . град.
Полученное уравнение (3.3.14) используется для расчета константы равновесия Кр реакций между веществами, для которых имеются стандартные данные.
Таким образом, чтобы рассчитать константу равновесия или величину DG0T для какой-либо реакции, необходимо знать:
1. Стандартные энтропии всех веществ при 298 К
2. Стандартные энтальпии образования всех участников реакции при 298 К 2. Коэффициенты а, в, с, с/ в уравнении зависимости теплоемкости от температуры всех участников реакции в интервале температур от 298 К до Т (для вычисления Dа, Dв …).
3. Коэффициенты М0, М1, М2, М –2 для данной температуры Т.
Если температура Т не очень сильно отличается от 298 К, то можно считать, что  и
и  , следовательно, DСр @ 0. В этом случае уравнение (20) принимает вид:
, следовательно, DСр @ 0. В этом случае уравнение (20) принимает вид:
 и Dа = Dв = Dс = Dс/ = 0
и Dа = Dв = Dс = Dс/ = 0
Для более точного расчета можно применять уравнение следующего вида:
 (3.3.15)
(3.3.15)
Если изменение теплоемкости (Ср) не равно нулю, но практически не зависит от температуры, то вместо Dа в последнем уравнении (3.3.15) подставляют DСр, т.е. изменение теплоемкости системы при реакции, рассчитанное по средним теплоемкостям.
Дата добавления: 2018-02-15; просмотров: 5858; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 (3.3.1)
(3.3.1)