Оптимизация режимов резания методом линейного программирования.
В основе метода лежит построение математической модели, процесса резания, включающей в себя совокупность технических ограничений, которые в наибольшей степени определяют описываемый процесс и оценочную функцию (критерий оптимальности).[2,4]
Расчет оптимальных режимов
Период стойкости инструмента Т,мин
(10.11.)
Так как 
, то для оптимизируемых параметров и получим условие, когда стойкость будет не менее нормативной
(10.12.)
Мощность электродвигателя главного движения станка
(10.13.)
получим 
, (10.14.)
Прочность механизма подач станка
(10.15.)
Прочность инструмента
(10.16.)
где:
h – толщина твердосплавной пластинки
Жесткость заготовки
(10.17.)
d - допуск на размер, мм;
Е – модуль упругости, МПа;
Dпр – приведенный диаметр ступенчатого вала, мм;
L3 – длина заготовки, мм;
ХР – расстояние от правого торца до места приложения силы, мм;
Жесткость инструмента
где: (10.18)
В – ширина резца, мм;
М – высота резца, мм;
Lвр – вылет резца. Мм;
Шероховатость обработанной поверхности
(10.19.)
где: r – радиус при вершине резца, мм;
|
|
|
Rz – средняя высота неровностей, мкм;
Наименьшая допустимая скорость резания
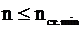(10.20.)
Наибольшая допустимая скорость резания
(10.21.)
Наименьшая допустимая подача
(10.22.)
11. Наибольшая допустимая подача
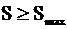(10.23.)
Приняв X1=ln n и X2=ln(100S)
Получаем систему неравенств
(10.24)
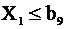
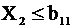
Преобразование технических ограничений к линейному виду и представление их в виде неравенств в совокупности с оценочной функцией дает математическую модель процесса резания металлов (10.24).
Применительно к математической модели (10.24.) задача определения оптимального режима резания сводится к отысканию среди всевозможных неотрицательных значений Х1 и Х2 системы таких значений Х1опт и Х2опт, при которых оценочная функция принимает максимальное значение Fmax.
Определение оптимальных значений Х1опт и Х2опт может производиться с использованием численных методов линейного программирования с применением ЭВМ. Эта же задача может быть решена графическим методом. В этом случае каждое техническое ограничение представляется граничной прямой, которая определяет полуплоскость , где возможно существование решение системы неравенств. Граничные прямые, пересекаясь, образуют многоугольник решений АВСД (рис.46), внутри которого любая точка удовлетворяет всем без исключения неравенствам. Для определения оптимальных значений Х1опт и Х2опт под углом 450 к осям Х1и Х2 строится вектор максимизации М для оценочной функции F, которая изображается прямой (штриховая линия), перпендикулярной этому вектору. В точке Р, где прямая оценочной функции коснется многоугольника решений, функция принимает минимальное значение F0 max. Координаты этой точки являются оптимальными значениями Х1опт и Х2опт, они определяются графически (рис. 46) [2,3,5].
|
|
|
Рис 46. Графическое построение математической модели определения оптимальных режимов резания.
Численные значения оптимального режима резания вычисляются по следующим зависимостям
n=eX1 (10.25) 
(10.26)
(начало)
Анализ математической модели задачи определения оптимальных режимов резания при чистовом точении
При изучении процесса чистового точения возникает задача максимизации функции [ 2]
|
|
|
F=nS (10.27)
при ограничениях
(10.28)
(10.29)
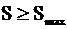(10.30)
(10.31)
(10.32)
(10.33)
Здесь
n – частота вращения шпинделя (об/мин)
S – подача (мм/об)
YV – безразмерный коэффициент [1])
CV - коэффициент [1]
XV – безразмерный коэффициент [1]
D – диаметр детали (мм)
T – стойкость инструмента
m – безразмерный коэффициент [1]
t – глубина резания (мм)
KiV - коэффициент [1]
Smin , Smax – соответственно наибольшая и наименьшая глубина подачи, допускаемые кинематикой станка (мм/об)
nст.min , nст. max– соответственно наибольшая и наименьшая частота вращения, допускаемые кинематикой станка (об/мин)
r – радиус при вершине резца (мм)
Ra – шероховатость, то есть средняя высота неровностей (мкм).
Целевая функция (10.27) и ограничения (10.28- 10.33) являются нелинейными, что усложняет задачу оптимизации. Чтобы упростить эту задачу мы прологарифмируем почленно соотношения (10.28-10.33) (натуральные логарифмы) (е =2,71828).
X1=ln n , X2=ln(100S) (10.34)
|
|
|
Придем к линейной задаче максимизации функции
При ограничениях
( 10.35)
Здесь W= ln (100F)
b1 = ln 1000 Cv Kv 100y ,
π D T m t x
b2 = ln (100 Smin ),
b3 = ln (100 Smax ),
b4 = ln (ncm. min ),
b5 = ln (ncm. max ),
b6 = ln (100√r2 – (r –0,005* Ra)2 ) (10.36)
В дальнейшем решение этой задачи аналогично предыдущему.
Варианты практических заданий по определению оптимальных режимов резания при чистовом точении даны в разделе N 3 (Работа N4) .
(начало)
Вопросы для самоконтроля
10.4.1.Что означает понятие “целевая функция?”.
10.4.2. Какие режимы резания являются оптимальными? Каковы критерии оптимальности?
10.4.3. В чем суть метода линейного программирования?
10.4.4. Принимая Х1=ln n, почему мы принимаем X2=ln(100 S)?
10.4.5. В чем суть графического метода решения задачи линейного программирования?
Литература
1. Справочник технолога-машиностроителя /Под ред. Косиловой А.Г. и Мещерякова Р.К. Т 2. - М.: Машиностроение. 1986. 495с.
2. Аверченко В.И. Оптимизация технологических процессов в САПР ТП. Брянск: БИТМ, 1987. 108с.
3. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986. – 319с., ил.
4. Аверченков В.И. и др. САПР технологических процессов, приспособлений и режущих инструментов: Учеб. пособие для вузов. – Мн.: Высш. шк., 1993 – 288с., ил.
5. Сборник задач и упражнений по технологии машиностроения: Учеб. пособие для машиностроительных вузов / В.И. Аверченков, О.А. Горленко и др.; Под общей ред. О.А. Горленко. – М.: Машиностроение, 1988. – 192с., ил.
Дата добавления: 2018-02-15; просмотров: 1603; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!