Построения фрагмента локального сплайна

Тема: «Квадратичные и кубические сплайны»

Выполнил: студент гр.  624  

Корнилов М. М.  

______________ 2015 г. _____________ /_____________/

          (дата)                                          (подпись студента)             (Расшифровка подписи)

                                      Руководитель: Ширков П.Д.

                                          Оценка руководителя ________________________

Дмитров

2015 г.

Содержание

Введение…………………………………………………………….……….3

1. Сплайн……………………………………………....………...……….4

1.1 Построения фрагмента локального сплайна…………………………..6

1.2 Классификация сплайнов……………………….………………………8

1.3Краевые условия…………....……………………………...………...…11

1.4Форма представления.………………………………………………....12

2. Кубический сплайн…………………………………….……………14

2.1. Построение……………………………..………………………………15

2.2 Реализация на языке C++…..………………………………..…………16

2.3 Реализация на языке C# Платформа .NET…..…..……………………19

2.4 Реализация на Python 2.7…..……………………………………......…22

3. Квадратичный сплайн……………………………………………...24

3.1 Квадратичный сплайн дефекта ………………………………...……..25

3.2Формирование систем………………………………………………...…..26

4 Заключение……………………………………………………...……27

5.Список литературы………………………………………………….28

Ведение

Сплайн — функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим многочленом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.

В современном понимании сплайны — это решения многоточечных краевых задач сеточными методами.

Сплайны имеют многочисленные применения, как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах системах компьютерного моделирования.

 Сплайны двух аргументов называют би-сплайнами (например, бикубический сплайн), которые являются двумерными сплайнами, моделирующими поверхности. Их часто путают с B-сплайнами (базисными сплайнами), которые являются одномерными и в линейной комбинации составляют кривые — каркас для «натягивания» поверхностей. Также из базисных сплайнов, возможно, составить трёхмерную конструкцию для моделирования объёмных тел.

Сплайн

Сплайном (англ. spline) называли гибкую металлическую линейку — универсальное лекало, которое использовали чертёжники для соединения точек на чертеже плавной кривой, то есть для графического исполнения интерполяции.

Более того, кривая, описывающая деформацию гибкой линейки, зафиксированной в отдельных точках, является сплайном. Итак, имеется физическая модель сплайн-функции (или, наоборот, сплайн-функция является математической моделью гибкой линейки). Интуитивный подход к использованию кусочных функций в задачах аппроксимации встречался в математике в течение длительного времени. Физической моделью, называемой механической аналогией сплайна, является многоопорная балка, не испытывающая внешней нагрузки, а деформации которой вызваны внутренними реакциями на заданные смещения опор в фиксированные узлы. Математически данная модель описывается дифференциальным уравнением деформации балки и является многоточечной краевой задачей, для решения которой был применён известный в то время сеточный метод, который получил решение именно в таком виде, называемом сегодня сплайном. Но, как отмечает советский учёный Николай Корнейчук, вторжение сплайнов в теорию приближения произошло из-за задачи интерполяции, благодаря их хорошим вычислительным и аппроксимативным свойствам. Сплайны обладают исключительно хорошими аппроксимативными свойствами, универсальностью и обеспечивают простоту реализации вычислительных алгоритмов, полученных на их основе. При этом алгоритмы построения сплайнов совпадают с алгоритмом метода конечных элементов, который является основным промышленным методом прочностного анализа в системах автоматизированного проектирования (САПР).

Теория интерполяции сплайнами и сам термин сплайн ведут свой отсчёт со статьи Айзека Шонберга (англ. Isaac Jacob Schoenberg) 1946 года. Особенно интенсивное её развитие произошло в 50-70 годы. В настоящее время традиционной прикладной сферой использования интерполяционных сплайнов стали САПР. Однако потенциальные возможности сплайнов значительно шире, чем просто описание некоторых кривых.

В реальном мире большое количество физических процессов по самой своей природе являются сплайнами. В механике это деформация гибкой пластины или стержня, зафиксированных в отдельных точках; траектория движения тела, если сила, действующая на него меняется ступенчато (траектория искусственного космического объекта с активными и инерционными отрезками движения, траектория движения самолёта при ступенчатом ​​изменении тяги двигателей и изменении профиля крыла и т. д.).

В термодинамике это теплообмен в стержне, составленном из фрагментов с различной теплопередачей. В химии — диффузия через слои различных веществ. В электричестве — распространение электромагнитных полей через разнородные среды.

Как следует из определения, для построения сплайна, состоящего из фрагментов, требуется найти такие значения числовых параметров для каждого фрагмента — полинома степени 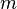, которые обеспечат непрерывность в узлах, как самой функции, так и необходимых производных. Так, всего следует определить параметров. С учётом условия интерполяции и непрерывности первых двух производных определение параметров сводится к решению системы, состоящей из линейных уравнений. Как правило, значения коэффициентов для отрезков полиномов непосредственно не рассчитываются.

Для определения интерполяционного сплайна с непрерывной первой производной достаточно рассчитать значение первой производной в узлах. Способ определения производных в узлах сплайна определяет широкое разнообразие интерполяционных сплайнов. Часто производные определяются не как константы, а как некоторые зависимости от интерполируемой функции и сетки интерполяции.

Если значение первой производной в узлах рассчитывать исходя из условия непрерывности второй производной (решая систему, составленную из n линейных уравнений), то сплайн будет иметь две непрерывные производные. Такой способ построения сплайна, как и сам сплайн называют глобальным, поскольку при определении каждого из его коэффициентов учитывается всё множество узлов интерполяции.

В других случаях, для определения отдельного коэффициента учитываются только ближайшие узлы интерполяции и такие способы построения, как и сами сплайны, называют локальными. Параметры фрагмента такого сплайна можно определить независимо от других фрагментов.

Построения фрагмента локального сплайна

Простым условием построения фрагмента локального сплайна является условие равенства полинома на концах отрезков соответствующим значениям интерполируемой функции.

Для простейшего сплайна — ломаной — этого условия вполне достаточно. Два коэффициента прямой однозначно определяются из двух уравнений. Такой сплайн является локальным. Для полиномов высших степеней следует добавить дополнительные условия таким образом, чтобы общее число уравнений было равно числу коэффициентов полинома. Так, для сплайна 3-й степени таким условием является равенство 1-й производной на концах отрезка некоторому значению, определяемому для соседних участков одинаковым образом (в формулах (2) через приближённое значение производной функции).

Система из 4-х уравнений.

позволяет однозначно определить четыре коэффициента полинома. Для полинома 5-й степени следует добавить условие равенства 2-й производной на концах отрезка и т. д. Из сказанного должно быть ясно, почему сплайны строят в основном из полиномов нечётных степеней (с чётным количеством коэффициентов).

Для полиномов чётных степеней при сборке системы (3):

· остаётся неопределённой производная в одном из концов отрезка;

· и условие равенства производных (гладкости кривой) не выполниться.   

Поэтому для полинома 2-й степени невозможно достичь равенства 1-й производной в точках стыка, а для 4-й степени — 2-й производной и т. д.

Для построения сплайнов с чётными степенями искусственно добавляют дополнительные условия, чтобы сформировать систему уравнений, подобную (3). Если производные полинома сплайна определяются также, как соответствующие производные интерполируемой функции, сплайн называется, является эрмитовым.

Существуют локальные методы построения сплайнов Бесселя и Акими.

В основном, когда речь идет о сплайнах, то имеют в виду сплайны, построенные из алгебраических полиномов. Именно к ним относится приведённое выше определение. Именно эти сплайны являются наиболее изученными. Однако, сплайн может состоять из фрагментов функций любого класса. Рассмотрено построение таких сплайнов и исследуются их свойства. Автор не даёт общего определения построенных сплайнов. Очевидно, что для любых классов функций, из которых состоит сплайн, приведённое в начале статьи определение не совсем подходит. Например, если сплайн состоит из отрезков экспоненты, то понятие дефекта сплайна теряет смысл. Хотя количество непрерывных производных останется важной характеристикой. Построение сплайна, фрагментами которого являются разрывные функции (рациональные функции, функции Паде), несколько выходит за рамки сплайновой идеи, поскольку одним из основных преимуществ сплайнов является их гладкость. Если произвольно расширять такие конструкции, то стираются различия сплайнов от кусковых функций. Другим преимуществом сплайнов является эффективность вычислений. Чрезмерное усложнение фрагментов существенно снижает преимущество сплайнов перед классическими функциями.

Для сплайнов характерны следующие признаки: сплайн состоит из фрагментов — функций одного класса, которые отличаются только своими параметрами, на соседние фрагменты в точках стыковки накладываются определенные условия, которые сводятся к непрерывности значений и некоторых первых производных. Сплайны — направление прикладной математики, которое интенсивно развивается. В Интернете содержится обширная библиография по сплайнам.

Классификация сплайнов

Как отмечалось выше, существует большое количество конструкций, которые называют сплайнами. Поэтому необходимо внести определенную классификацию в это многообразие, имея целью выделить те признаки, которые позволят выбрать сплайны годные для конкретной прикладной задачи.

Назначение сплайнов. По назначению можно выделить три основные группы сплайнов: «интерполяционные сплайны» или «функциональные сплайны» — проходящие точно через заданные точки, «сглаживающие сплайны» — проходящие через заданные точки с учетом погрешностей их определения; «корреляционные сплайны» — проходящие через корреляционное множество точек и отображающие его генеральную зависимость (тренд, регрессию). Интерполяционные и функциональные сплайны используют в задачах геометрического моделирования, например, задания обводов корпусов водных и воздушных судов. Сглаживающие сплайны используют чаще всего для описания зависимостей физических экспериментов с известной погрешностью измерений. Корреляционные сплайны используют в качестве нелинейных графиков регрессии, простейшими из которых можно считать описание зависимости ступенчатой и кусочно-линейной функцией (сплайнами нулевой и первой степени).

Вид фрагментов сплайна. То, что сплайн состоит из фрагментов одинакового вида, является одним из ключевых признаков, что отличает его от других кусковых функций. Однако существуют комбинированные сплайны, состоящие из фрагментов различных сплайнов.

Самые известные сплайны — состоящие из фрагментов — алгебраических полиномов не выше заданной степени. Как правило, это кубические полиномы, или полиномы нечётных степеней: первой, третьей (кубический), пятой степени. Более высокие степени применяют редко из-за усложнения расчетов и сложностей, описанных в предыдущем разделе. Основным их преимуществом является простота расчетов и анализа. Недостатком является то, что относительно мало реальных физических процессов соответствуют этой зависимости.

Экспоненциальные сплайны. Если гибкую металлическую линейку, зафиксированную в узлах, натянуть, то решением дифференциального уравнения будет не алгебраический полином, а экспонента. Поэтому такие сплайны называют также напряженными. Экспонента описывает многие физические процессы в динамических системах. Недостатком является трудоёмкость расчета.

Аналогично по механической аналогии с металлической линейкой, представляющей собой расчетную модель балки, получаются сплайны переменной жесткости, описанные в работах Снигирева В. Ф. и Павленко А. П. Первоначально такие сплайны называли вырождающимися или логарифмическими, так как решение исходного сплайнового дифференциального уравнения, представляющее собой фрагмент сплайна, будет содержать натуральные логарифмические функции. Жесткость в них может выступать как весовая, если она заранее задана, так и как управляющая функция, которая отыскивается из условий минимума функционала энергии оператора исходного сплайнового уравнения, аналогичного полной потенциальной энергии деформации линейки (балки). Функция жесткости позволяет управлять формой сплайна. В случае, когда функция жесткости является управляющей функцией, то такие сплайны называют сплайнами минимальной жесткости.

Тригонометрическими являются сплайны, фрагменты которых описываются тригонометрическими полиномами. Имеют достаточно сложные расчетные выражения. Более пятидесяти различных по виду фрагментов сплайнов описаны в работах Б. А. Попова.

Также существуют рациональные сплайны и сплайны Паде. Их особенностью является возможность разрыва производных на фрагментах, при непрерывности в узлах. М. Ансерме строит фракциональные сплайны, где фрагменты заданы с помощью гамма-функции.

Целесообразность применения фрагментов определенного вида основана на конкретных условиях задачи и ограничениях реализации. Как правило, основное требование — это достижение заданной точности интерполяции при приемлемых затратах времени и ресурсов на реализацию. Удачный выбор фрагментов, который соответствует характеру процесса, позволяет сократить время вычислений и требуемый объём памяти.

Число фрагментов. Очевидно, что минимальное число фрагментов — один. Классическое определение сплайна ограничивает число фрагментов определенным числом на конечном отрезке. Однако можно строить сплайны и с бесконечным числом фрагментов, а реально эти методы и алгоритмы, которые не нуждаются в информации об определенном количестве фрагментов. Представителями этих сплайнов являются кардинальные сплайны, исследованные Шенбергом. Для построения сплайнов с неограниченным числом фрагментов лучше подходят локальные сплайны.

Ширина фрагментов. Следует выделить сплайны с равной шириной фрагментов. Это позволяет значительно упростить расчетные выражения, ускорить работу алгоритмов и снизить затраты на реализацию. Определенного упрощения можно достичь за счёт применения фрагментов с кратной шириной. Существуют сплайны с нулевой шириной фрагментов (Де Бур). Это приводит к кратности узлов и возможности приближать сплайны с неразрывными фрагментами разрывных функций. Расчетные выражения получают в результате предельных переходов. Сплайны могут иметь также фрагменты с бесконечной шириной. Эти фрагменты должны быть крайними. Иногда это позволяет естественно задать краевые условия. Строго говоря, ширина фрагментов зависит от выбора параметра — аргумента сплайн-функции, а для этого требуется решать отдельную задачу параметризации. Идеальным выбором в качестве параметра является длина интерполируемой функции, которая не всегда известна, поэтому существует множество способов решения этой задачи.

Условия стыковки фрагментов. Еще один важный признак, что отличает сплайны. Когда идет речь о сплайнах, как правило, считают, что фрагменты стыкуются гладко. То есть обеспечивается непрерывность значений и первой производной. Понятие дефекта сплайна связано с числом непрерывных производных, которые имеет функция-фрагмент определенного вида и числом производных, непрерывность которых гарантирована в узлах. Экспонента, синусоида имеют бесконечное число производных. Для них это понятие не имеет смысла. Поэтому удобнее говорить прямо о числе производных, непрерывность которых гарантирована в узлах сплайна. Практически речь идет о непрерывности значений и первой, максимум второй производной. Разрыв второй и высших производных визуально не заметно, поэтому учитывается редко. Понятно, что первая производная в точках стыка может задаваться по-разному. Наиболее распространены два приёма. Значение первой производной выбирается так, чтобы обеспечить непрерывность второй (глобальные кубические сплайны минимального дефекта). Первая производная равняется первой производной.

Краевые условия

Имеется 4 типа классических краевых условий и ряд неклассических. Если сплайны имеют ограниченное число фрагментов, то, естественно, у них отсутствуют крайние фрагменты слева и справа, поэтому крайние узлы не с чем стыковать. Исключением являются лишь периодические сплайны, которые имеют естественное продолжение (3-й тип классических краевых условий). Иногда естественными называют краевые условия с нулевой производной, хотя никаких оснований считать их более естественными, чем другие, нет, но для кубического сплайна естественные (натуральные) краевые условия являются частным случаем 2-го типа классических краевых условий, задающего вторые производные на краях сплайна. В этом случае приравнивание вторых производных к нулю высвобождает края металлической линейки от нагружения изгибающим моментом, что естественным образом и происходило бы при прикладывании ее к фиксированным (заданным) узлам в физическом пространстве. В 1-м типе классических краевых условий задают первые производные (касательные) на краях сплайна; во 2-м типе — задают вторые производные(кривизну); 3-й тип используется для интерполяции замкнутых или периодических линий и заключается в стыковке крайних фрагментов сплайна; 4-й тип используется когда на краях сплайна неизвестны ни первая, ни вторая производные и заключается в стыковке соседних пар крайних фрагментов (1-го со 2-м и последнего с предпоследним) по третьим производным, что на практике реализуется в проведении по узлам пар соседних крайних фрагментов функции, аналогичной одному фрагменту сплайна (у полиномиального сплайна — полинома той же степени, что и фрагмент сплайна).

Используются различные комбинации краевых условий, которые сводятся к данным 4-м типам классических условий. Далее приведены некоторые варианты, сводящиеся к классическим краевым условиям. Если сплайн имеет фрагменты одинаковой ширины, считают недостающие фрагменты той же ширины. Другой вариант — это считать недостающие фрагменты продлёнными в бесконечность. Преимущество такого подхода в возможности экстраполяции. Можно считать ширину фрагментов нулевой. Расчетные выражения получают предельными переходами. Если взглянуть на краевые условия с точки зрения формирования сплайна из базисных функций, то они сводятся к продолжению соответствующих локальных базисных функций. Значение краевые условия имеют при обработке изображений и в задачах с экстраполяцией.

Форма представления.

Функции, задающие фрагменты сплайна, как правило, зависят от множества параметров, благодаря которым они меняют свою форму. Значения параметров на каждом из фрагментов индивидуальны. Эти параметры могут задавать конкретный сплайн. Для полиномиальных сплайнов это полиномиальные коэффициенты. Так, сплайн можно представить множеством параметров функций на каждом из фрагментов. Назовем это представление пофрагментным. Такое представление является наглядным, часто имеет явный физический смысл. Но число параметров является чрезмерным. Так, для кубического сплайна необходимо иметь 4 * (r-1) параметров (r — число узлов сплайна). Данное представление получается в результате неопределенного интегрирования фрагмента исходного сплайнового дифференциального уравнения и называется аналогичной кусочно-полиномиальной формой (pp-формой) по аналогии с полиномиальными сплайнами. Для явного выражения коэффициентов через уже известные значения координат узловых точек, применяют разложение аналогичной кусочно-полиномиальной формы на базисные функции путем подстановки ее в краевые условия Эрмита (граничные условия фрагмента сплайна, условия интерполирования и опирания на производные). В результате получается базисная форма (B-форма) сплайна. Такое представление сплайна является значительно более компактным и записывается через базисные сплайн-функции в виде:

Где:

— базисные сплайн-функции (как правило локальные),

— числовые коэффициенты, задающие вес базисных функций при формировании сплайна, физическим смыслом которых являются обобщенные (линейные и угловые) перемещения металлической линейки в узлах. Число параметров, задающих сплайн, равно числу узлов сплайна.

Между параметрами функции на фрагменте и коэффициентами полинома-сплайна существует зависимость, что позволяет с одними коэффициентами находить другие, хотя формулы могут иметь достаточно сложный вид.

Содержание коэффициентов сплайна. Как отмечалось в предыдущем пункте, содержание параметров сплайна при пофрагментном представлении определяется типом функции. При полиномиальном представлении следует выделить случай, когда коэффициенты имеют тот же физический смысл, что и входные данные. То есть, коэффициенты являются значениями сплайна в узлах. Такую форму называют Лагранжевой, по аналогии с полиномом Лагранжа. Следует заметить, что базисные сплайны этой формы равны единице в центральном узле и нулю во всех остальных.

Коэффициенты интерполяционных и функциональных сплайнов всегда содержат значения координат заданных точек, вытекающие из условий интерполирования. А так же в зависимости от условий опирания на производные, содержат значения соответствующих производных на границах фрагмента сплайна (в узловых точках). Как правило, при записи таких условий фрагмент сплайна на его границах опирают на первые или вторые производные. Опирание фрагмента сплайна на первые производные явно отражает физический смысл, так как первые производные (касательные) — это угловые перемещения (повороты) металлической линейки относительно поперечной оси. Опирание сплайна на вторые производные применяют для упрощения вида расчетных выражений с целью уменьшения ошибок при их ручной перезаписи, однако в некоторых случаях использование таких выражений в каких-либо дополнительных условиях может приводить к тривиальным решениям.

Особые сплайны. В ряде случаев рассматривают функции, которые находятся близко к границе между сплайнами и обычными функциями, а также сплайнами и кусковыми функциями. К примеру, это сплайны, состоящие из двух фрагментов. Имеют упрощенный вариант построения, но особое внимание следует уделять краевым условиям.

К особым сплайнам можно отнести многомерный ортогональный нормированный сплайн, описывающий нелинейную модель искусственного нейрона (сплайн-модель Хакимова). используемый для моделирования зависимости функции от совокупности множества аргументов.

Кубический сплайн

Теорема:Для любой функции и любого разбиения отрезка существует ровно один естественный сплайн S(x), удовлетворяющий перечисленным выше условиям.

Эта теорема является следствием более общей теоремы Шёнберга-Уитни об условиях существования интерполяционного сплайна.

Некоторая функция f(x) задана на отрезке , разбитом на части , . Кубическим сплайном дефекта 1 называетсяфункция , которая:

-на каждом отрезке является многочленом степени не выше третьей;

-имеет непрерывные первую и вторую производные на всём отрезке ;

-в точках выполняется равенство , т. е. сплайн интерполирует функцию f в точках .

Для однозначного задания сплайна перечисленных условий недостаточно, для построения сплайна необходимо наложить какие-то дополнительные требования.

Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:

Построение

Обозначим:   

На каждом отрезке функция есть полином третьей степени , коэффициенты которого надо определить. Запишем для удобства в виде:

Тогда

Условия непрерывности всех производных до второго порядка включительно записываются в виде

а условия интерполяции в виде

Отсюда получаем формулы для вычисления коэффициентов сплайна:

Если учесть, что , то вычисление можно провести с помощью метода прогонки для трёхдиагональной матрицы.

2.2 Реализация на языке C++

#include <cstdlib>

#include <cmath>

#include <limits>

 class cubic_spline

{

private:

       // Структура, описывающая сплайн на каждом сегменте сетки

       struct spline_tuple

       {

                   double a, b, c, d, x;

       };

       spline_tuple *splines; // Сплайн

       std::size_t n; // Количество узлов сетки

       void free_mem(); // Освобождение памяти

 public:

       cubic_spline(); //конструктор

       ~cubic_spline(); //деструктор

       // Построение сплайна

       // x - узлы сетки, должны быть упорядочены по возрастанию, кратные узлы запрещены

       // y - значения функции в узлах сетки

       // n - количество узлов сетки

       void build_spline(const double *x, const double *y, std::size_t n);

       // Вычисление значения интерполированной функции в произвольной точке

       double f(double x) const;

};

 cubic_spline::cubic_spline() : splines(NULL)

{

}

cubic_spline::~cubic_spline()

{

       free_mem();

}

 void cubic_spline::build_spline(const double *x, const double *y, std::size_t n)

{

       free_mem();

       this->n = n;

       // Инициализация массива сплайнов

       splines = new spline_tuple[n];

       for (std::size_t i = 0; i < n; ++i)

       {

                   splines[i].x = x[i];

                   splines[i].a = y[i];

       }

       splines[0].c = 0.;

 // Решение СЛАУ относительно коэффициентов сплайнов c[i] методом прогонки для трехдиагональных матриц

       // Вычисление прогоночных коэффициентов - прямой ход метода прогонки

       double *alpha = new double[n - 1];

       double *beta = new double[n - 1];

       double A, B, C, F, h_i, h_i1, z;

       alpha[0] = beta[0] = 0.;

       for (std::size_t i = 1; i < n - 1; ++i)

       {

                   h_i = x[i] - x[i - 1], h_i1 = x[i + 1] - x[i];

                   A = h_i;

                   C = 2. * (h_i + h_i1);

                   B = h_i1;

                   F = 6. * ((y[i + 1] - y[i]) / h_i1 - (y[i] - y[i - 1]) / h_i);

                   z = (A * alpha[i - 1] + C);

                   alpha[i] = -B / z;

                   beta[i] = (F - A * beta[i - 1]) / z;

       }

 splines[n - 1].c = (F - A * beta[n - 2]) / (C + A * alpha[n - 2]);

       // Нахождение решения - обратный ход метода прогонки

       for (std::size_t i = n - 2; i > 0; --i)

                   splines[i].c = alpha[i] * splines[i + 1].c + beta[i];

       // Освобождение памяти, занимаемой прогоночными коэффициентами

       delete[] beta;

       delete[] alpha;

       // По известным коэффициентам c[i] находим значения b[i] и d[i]

       for (std::size_t i = n - 1; i > 0; --i)

       {

                   double h_i = x[i] - x[i - 1];

                   splines[i].d = (splines[i].c - splines[i - 1].c) / h_i;

                   splines[i].b = h_i * (2. * splines[i].c + splines[i - 1].c) / 6. + (y[i] - y[i - 1]) / h_i;

       }

}

double cubic_spline::f(double x) const

{

       if (!splines)

                   return std::numeric_limits<double>::quiet_NaN(); // Если сплайны ещё не построены - возвращаем NaN

        spline_tuple *s;

       if (x <= splines[0].x) // Если x меньше точки сетки x[0] - пользуемся первым эл-том массива

                   s = splines + 1;

       else if (x >= splines[n - 1].x) // Если x больше точки сетки x[n - 1] - пользуемся последним эл-том массива

                   s = splines + n - 1;

       else // Иначе x лежит между граничными точками сетки - производим бинарный поиск нужного эл-та массива

       {

                   std::size_t i = 0, j = n - 1;

                   while (i + 1 < j)

                   {

                                std::size_t k = i + (j - i) / 2;

                                if (x <= splines[k].x)

                                            j = k;

                                else

                                            i = k;

                   }

                   s = splines + j;

       }

       double dx = (x - s->x);

       return s->a + (s->b + (s->c / 2. + s->d * dx / 6.) * dx) * dx; // Вычисляем значение сплайна в заданной точке.

}

 void cubic_spline::free_mem()

{

       delete[] splines;

       splines = NULL;

}

Мы поможем в написании ваших работ!