Площадь криволинейного сектора
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат имеет вид p = f(φ), где p – длина радиус – вектора, соединяющего полюс с произвольной точки кривой, а φ – угол наклона этого радиус – вектора к полярной оси. Тогда площадь криволинейного сектора может быть найдена по формуле:
Площадь криволинейной трапеции
Пусть функция 
неотрицательна и непрерывна на отрезке 
. Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью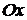 
, слева и справа – прямыми 
и 
(рис 5) вычисляется по формуле
Формула 5. Площадь криволинейной трапеции
Пример 1. Найти площадь фигуры, ограниченной линией 
и осью .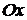
Решение. Графиком функции 
является парабола, ветви которой направлены вниз. Построим ее график (рис 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью 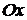(прямой 
). Для этого решаем систему уравнений 
Получаем: 
, откуда 
, 
; следовательно, 
, 
.
Рисунок 3. График функции y=2x-x2+8
Площадь фигуры находим по формуле (формула 5):
(кв.ед.).
Если функция неположительна и непрерывна на отрезке 
, то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью 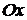, слева и справа – прямыми 
и 
, вычисляется по формуле
|
|
|
Формула 6. Отрицательная площадь криволинейной
В случае если функция 
непрерывна на отрезке 
и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис 4) равна алгебраической сумме соответствующих определенных интегралов:
Формула 7. Площадь фигуры
Рисунок 4. криволинейная трапеция
Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема. Если функция 
непрерывна на отрезке 
и 
– какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
Формула 4. Формула Ньютона-Лейбница
Формула называется формулой Ньютона–Лейбница. Разность 
принято записывать следующим образом: 
,
где символ 
называется знаком двойной подстановки.
Таким образом, формулу (формула 4) можно записать в виде:
.
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную 
для подынтегральной функции 
; на втором – находится разность 
значений этой первообразной на концах отрезка .
|
|
|
Пример 1. Вычислить интеграл 
.
Решение. Для подынтегральной функции 
произвольная первообразная имеет вид 
. Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид: 
. Тогда 
.
Дата добавления: 2018-02-15; просмотров: 848; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!