Геометрический смысл определенного интеграла. Пусть на отрезке задана непрерывная неотрицательная функция

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (Рис1).

Рисунок 1. Криволинейная трапеция

Определенный интеграл от неотрицательной функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа – отрезками прямых и , снизу – отрезком оси Ох.

Интегрирование по частям

Теорема. Пусть функции и 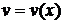имеют непрерывные производные на отрезке . Тогда имеет место следующая формула интегрирования по частям:

Формула 3. Интегрирование по частям

Доказательство.Так как , то функция является первообразной для функции . Тогда по формуле Ньютона–Лейбница получаем

, откуда

Пример 1. Вычислить .

Решение. Положим , отсюда . По формуле (формула 3) находим
.

Основные свойства определенного интеграла

1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: .

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

3. Если , то, по определению, полагаем

4. Постоянный множитель можно выносить за знак определенного интеграла:

5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

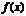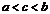6. Если функция интегрируема на и , то

7. (теорема о среднем). Если функция непрерывна на отрезке , то на этом отрезке существует точка , такая, что .

Длина дуги кривой

Пусть функция y = f(x) определена и непрерывна на отрезке [a; b] и кривая l- график этой функции. Требуется найти длину дуги плоской кривой l, заключенной между вертикальными прямыми (рис 5) x = a и x = b

Рисунок 5. Дуга плоской кривой

Под длиной дуги сначала понимаем длину ломаной A,M1,M2…Mn-1,B. Очевидно, что длина ломаной является лишь приближенным значением длины дуги. Если увеличивать число точек разбиения то длина ломаной будет стремиться к длине кривой АВ ( при этом разбиение необходимо производить таким образом, чтобы длина наибольшего частичного отрезка стремилась к нулю).

Если существует конечный предел ln при λ=max{Δx_k} → 0, то этот предел принимается за длину дуги l , а саму дугу называют спрямляемой т. е.

Формула 8. Формула конечного предела

Если конечный предел не существует, то длины дуги не существует, а сама кривая называется не спрямляемой.

Вычислим длину хорды Mk-1 M. Учтем, что координаты этих точек Mk-1(xk_-1; f(x_k-1)) и M_k (x_k;f(x_k )).

Тогда:

По теореме Лагранжа имеем:

Следовательно

Подставляя полученное выражение в формулу (формула 8), получаем

Формула 9. интегральная сумма для функции на отрезке [a; b]

В правой части равенства (формула 9) стоит интегральная сумма для функции 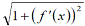на отрезке [a; b]

Предел такой суммы существует и равен определенному интегралу от этой функции на отрезке [a; b]

Таким образом, если функция f(x) имеет на отрезке [a; b] непрерывную производную, то дуга АВ -спрямляемая и ее длина l вычисляется по формуле

Дата добавления: 2018-02-15; просмотров: 1129; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!