Физический смысл определенного интеграла
Министерство образования Российской Федерации
«Ижевский государственный технический университет»
Факультет “ИВТ”
Кафедра “Вычислительные системы, комплексы и сети”
Реферат
По предмету: Математический анализ
На тему: «Определенные интегралы»
Выполнил: Вологжанин М.В. Группа Б01-781-1
Проверил(а): Возмищева Т.Г.
2011
Содержание
Содержание. 2
1. Понятие определенного интеграла. 3
2. Замена переменной в определенном интеграле. 5
3. Физический смысл определенного интеграла. 6
4. Геометрический смысл определенного интеграла. 6
5. Интегрирование по частям. 7
6. Основные свойства определенного интеграла. 8
7. Длина дуги кривой. 9
Площадь криволинейного сектора. 10
8. Площадь криволинейной трапеции. 11
9. Формула Ньютона–Лейбница. 12
10. Вычисление объема тела по площадя сечения. 14
11. Площадь поверхности тела вращения. 15
12. Длина дуги плоской кривой. 16
13. Объем тела вращения. 17
14. Несобственные интегралы от неограниченных функций. 19
Литература. 21
1. Понятие определенного интеграла
Пусть функция 
определена на отрезке 
, 
.
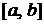Выполним следующие операции:
1. разобьем отрезок 
точками 
на n частичных отрезков 
.
2. в каждом из частичных отрезков 
, 
выберем произвольную точку 
и вычислим значение функции в этой точке: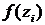 
.
|
|
|
3. найдем произведения 
, где 
– длина частичного отрезка , 
.
4. составим сумму
Формула 1. Интегральная сумма функции y=f(x)
Формула называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма 
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки 
, а высоты равны 
соответственно.
Обозначим через 
длину наибольшего частичного отрезка 
;
5. найдем предел интегральной суммы, когда 
.
Определение. Если существует конечный предел интегральной суммы (Формула 1) и он не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек 
в них, то этот предел называется определенным интегралом от функции на отрезке и обозначается 
.
Таким образом, 
В этом случае функция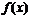 
называется интегрируемой на отрезке 
. Числа а, b называются нижним и верхним пределами интегрирования, 
– подынтегральной функцией, 
– подынтегральным выражением, 
– переменной интегрирования; отрезок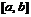 
называется промежутком интегрирования.
Теорема. Если функция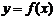 
непрерывна на отрезке , то она интегрируема на этом отрезке.
Замена переменной в определенном интеграле
|
|
|
Теорема. Пусть функция непрерывна на отрезке . Тогда, если:
1. функция 
и ее производная 
непрерывны при 
;
2. множеством значений функции 
при является отрезок ;
3. 
, 
, то справедлива формула
Формула 2. Замена переменной в определенном интеграле
Формула называется формулой замены переменной в определенном интеграле.
Заметим, что как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования 
и 
(для этого надо решить относительно переменной t уравнения 
и 
)).
На практике часто вместо подстановки используют подстановку 
. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 
, 
.
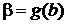Пример 1. Вычислить интеграл 
Решение. Введем новую переменную по формуле 
. Определим и 
. Возведя в квадрат обе части равенства , получим 
, откуда 
. Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы 
и 
. Получим: 
, откуда 
и, следовательно, 
; 
, откуда 
и, следовательно, 
.
|
|
|
Таким образом: 
.
Физический смысл определенного интеграла
Пусть точка движется прямолинейно вдоль числовой оси с непрерывно меняющейся скоростью V(t), t0 ≤ t ≤ T. Смещение точки за малый промежуток времени ∆tk = tk – tk-1 приближенно можно считать равным v(ξk) ∆tk, где ξk ∈ [tk-1,tk].
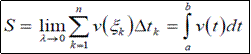
Тогда интегральная сумма 
представляет собой приближенное значение пути, пройденного точкой от момента времени t0 до T. В пределе при λ = max{∆t} → 0 получим точное значение этого пути S
Дата добавления: 2018-02-15; просмотров: 1142; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!