Однородная краевая задача для ЛОДУ второго порядка с

коэффициентами, зависящими от параметра (задача Штурма-Лиувилля). Собственные числа и собственные функции.

Оп.1. Однородной краевой задачей называется такая задача, для

которой правая часть краевых условий имеет нулевые значения, т.е. числа 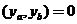,  или  равны нулю.

  Оп.2. Линейным дифференциальным оператором второго порядка с коэффициентами, зависящими от одного числового параметра , называется оператор вида

                                                                           (13)

  Оп.3. Линейным граничным дифференциальным оператором первого порядка называется опреатор вида

                                                                          (14)

здесь нижний индекс указывает на принадлежность к начальному  или конечному  значению координат точек интервала.

  Оп.4. Однородной краевой задачей для ЛОДУ второго порядка с коэффициентами, зависящими от обного числового параметра, называется краевая задача вида

                                                                    (15)

                                                                   (16)

состоящая в определении таких значений парметра , при которых поставленная задача имеет не тривиальное значение (задача Штурма-Лиувилля).

    Оп. 5. Значения параметра , прикоторых задача Штурма-Лиувилля имеет решения называются собствеными значениями  или собственными числами.

    Оп. 6. Функции-решения  задачи Штурма-Лиувилля, соответствующих собственным значениям (собственным числам), называ.тся собственными функциями.

Общая форма простейшей задачи Штурма-Лиувилля является такая, когда коэффициенты дифференциального оператора-степенные функции искомого параметра  

           (17)

где  - такие числа, дискиминант которых отрицательное число; это дает фундаментальные решения в виде экспонет и синус-косинусфункций, т.е. решение в форме

                                        (18)

произвольные  постоянные-функции параметра ,определяемые из детерминантного определяющего уравнения, составленного для заданного типа краевых условий для каждого фундаметального решения                                                                    

             (19)

и принимающего форму

                                                         (20)

в результате имеем одно трансцендентное (или тригонометрическое) детерминантное характеристическое уравнение для определения значений параметра :

- для краевых условий первого рода на обоих краях

                                     (21)

- для краевых условий второго родана обоих краях 

                                     (22)

- для краевых условий третьего рода на обоих краях                                   

       (23)

В первых двух случаях имеем тригонометрические уравнения, решения которых простые и дают счетное множество собственных чисел и собственных функций, а в третьем-уравнение трансцендентное, решение может быть определено, например, графически путем построения тангенсоиды и прямо и определения точек пересечения кривых; в результате также имеем счетное множество собственных чисел и собственных функций

 

 

Задача Штурма — Лиувилля

Задача Шту́рма — Лиуви́лля состоит в отыскании нетривиальных (т.е. отличных от тождественного нуля) решений на промежутке 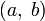однородного уравнения

удовлетворяющих однородным граничным условиям

и значений параметра , при которых такие удовлетворяющие указанным граничным условиям решения существуют.

Оператор здесь — это действующий на функцию линейный дифференциальный оператор второго порядка вида

(оператор Штурма — Лиувилля), — вещественный аргумент.

Функции предполагаются непрерывными на 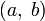, кроме того функции положительны на .

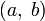Искомые нетривиальные решения называются собственными функциями этой задачи, а значения , при которых такое решение существует — её собственными значениями (каждому собственному значению соответствует собственная функция).

Свойства

Данная задача обладает рядом свойств:

· Существует бесконечное счетное множество собственных значений и соответствующая им бесконечная последовательность собственных функций. Все собственные значения можно занумеровать в порядке возрастания их абсолютной величины

· Все собственные значения задачи действительные.

· Каждому собственному значению соответствует с точностью до постоянного множителя только одна собственная функция.

· Рассмотрение комплекснозначных собственных функций не обогащает систему всех собственных функций, но добавляет в неё линейно зависимые элементы.

· В случае граничных условий и при выполнении условия все собственные значениякраевой задачи положительны .

· Собственные функции образуют на ортогональную с весом 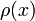систему :

 

 

---

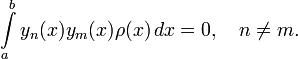
Дата добавления: 2018-02-15; просмотров: 443; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!