Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
ЗАДАЧИ КОШИ ДЛЯ ЛИНЕЙНОГО ОДУ 1 ГО ПОРЯДКА.
Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка, записанное в нормальной форме:

Областью определения уравнения называется область D определения правой части уравненияf(x,y), D ⊂ R2 .
Функция y = y(x) является решением задачи Коши
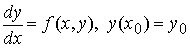
если y = y(x) дифференцируема на [a,b] , (x,y(x)) ∈ D для всех x из [a,b] , y(x0) = y0 , x0∈[a,b], и при подстановке в уравнение обращает его в тождество:

Фундаментальным результатом теории обыкновенных дифференциальных уравнений являетсятеорема существования и единственности решения задачи Коши:
Пусть функция f(x, y) и ее частная производная fy(x, y) непрерывны в некоторой области Dплоскости x0y и точка (x0, y0) принадлежит области D.
Тогда :
— в некоторой окрестности (x0 − δ,x0 + δ) точки x0 существует решение задачи Коши
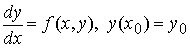
— если y = φ1(x) и y = φ2(x) два решения задачи Коши, то φ1(x) = φ2(x) на (x0 − δ,x0 + δ) .
Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x0,y0) области D проходит единственная интегральная кривая уравнения.
Бесконечное множество решений уравнения

можно рассматривать как однопараметрическое семейство функций y = φ(x; x0) — семействорешений задачи Коши
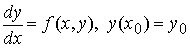
элементы которого различны для разных значений x0 . Иными словами область D"расслаивается" на интегральные кривые y = φ(x; x0) .
Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x0 . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.
|
|
|
ОДУ 2 порядка, правая часть которого не содержит явного[x]
Опр. Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов): 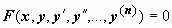 .
.  Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
 Опр. Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция
Опр. Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция 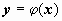 , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.
 Опр. Общим решением (общим интегралом) уравнения называется такое соотношение
Опр. Общим решением (общим интегралом) уравнения называется такое соотношение 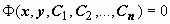 , что:
, что:
 1. Любое решение
1. Любое решение 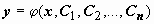 этого соотношения относительно y (для набора постоянных C1, C2, …, Cn из некоторой областиn-мерного пространства) является частным решением уравнения ;
этого соотношения относительно y (для набора постоянных C1, C2, …, Cn из некоторой областиn-мерного пространства) является частным решением уравнения ;
 2. Любое частное решение уравнения может быть получено из общего решения
2. Любое частное решение уравнения может быть получено из общего решения 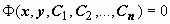 при некотором наборе постоянных C1, C2, …, Cn.
при некотором наборе постоянных C1, C2, …, Cn.
 Основную теорему - теорему о существовании и единственности решения задачи Коши для уравнения n-го порядка -мы сформулируем для записи уравнения в форме, разрешённой относительно старшей производной:
Основную теорему - теорему о существовании и единственности решения задачи Коши для уравнения n-го порядка -мы сформулируем для записи уравнения в форме, разрешённой относительно старшей производной:  .
.
 14.4.1. Постановка задачи Коши для уравнения n-го порядка: требуется найти решение уравнения
14.4.1. Постановка задачи Коши для уравнения n-го порядка: требуется найти решение уравнения
|
|
|
  ; ;
| (17) |
удовлетворяющее начальным условиям
 
| (18) |
где y0, y1, y2, …, yn-1 - заданные числа.
 В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x0, y0,) с заданным угловым коэффициентом y1.
В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x0, y0,) с заданным угловым коэффициентом y1.
 Теорема существования и единственности решения задачи Коши: Пусть функция f(x, y, p1, p2, …, pn-1) непрерывна и имеет непрерывные частные производные
Теорема существования и единственности решения задачи Коши: Пусть функция f(x, y, p1, p2, …, pn-1) непрерывна и имеет непрерывные частные производные 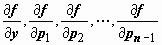 в некоторой области Dn + 1-мерного евклидового пространства переменных(x, y, p1, p2, …, pn-1), и пусть точка (x0, y0, y1, y2, …, yn-1) принадлежит области D. Тогда в некоторой окрестности точки x0 существует решение уравнения (17), удовлетворяющее начальным условиям (18). Это решение единственно.
в некоторой области Dn + 1-мерного евклидового пространства переменных(x, y, p1, p2, …, pn-1), и пусть точка (x0, y0, y1, y2, …, yn-1) принадлежит области D. Тогда в некоторой окрестности точки x0 существует решение уравнения (17), удовлетворяющее начальным условиям (18). Это решение единственно.
 14.4.2. Некоторые типы уравнений, допускающие понижение порядка.
14.4.2. Некоторые типы уравнений, допускающие понижение порядка.
 14.4.2.1. Уравнение вида
14.4.2.1. Уравнение вида  решается последовательным n-кратным интегрированием. Пример:
решается последовательным n-кратным интегрированием. Пример:

Переобозначив постояные, общее решение запишем в виде y = cos x + C1x3 + C2x2 + C3x + C4.
 14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения видаF(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y(k)(x). Тогда
14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения видаF(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y(k)(x). Тогда  z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид
z(n-k) = y(n)(x), и относительно z(x) уравнение примет вид  , т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x).
, т.е. будет уравнением n - k-го порядка. После нахождения z(x)последовательным интегрированием решается уравнение y(k) = z(x).
 Пример: решить задачу Коши:
Пример: решить задачу Коши:  .
.
 Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции
Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции  . Тогда
. Тогда  , и уравнение примет вид
, и уравнение примет вид  . Это - уравнение Бернулли; пусть z = uv, тогда
. Это - уравнение Бернулли; пусть z = uv, тогда  ,
,  ,
, 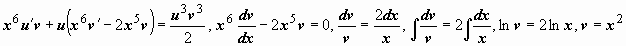 ,
, 
 следовательно,
следовательно, 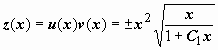 . Относительно y(x) - это уравнение
. Относительно y(x) - это уравнение  . Мы можем последовательно находить
. Мы можем последовательно находить  и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия
и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия  при x = 1 можно определить и знак частного решения, и значение постояннойC1:
при x = 1 можно определить и знак частного решения, и значение постояннойC1: 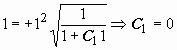 . Теперь
. Теперь  . Из условия
. Из условия 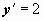 при x = 1 находим C2:
при x = 1 находим C2:  ; из условия y = 3 при x = 1 находим C3:
; из условия y = 3 при x = 1 находим C3:  . Окончательный ответ:
. Окончательный ответ:  .
.
 14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x.Порядок уравнения
14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x.Порядок уравнения  , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость
, не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость 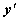 от y:
от y:  . Старшие производные y по xвычисляются по правилу дифференцирования сложной функции:
. Старшие производные y по xвычисляются по правилу дифференцирования сложной функции: 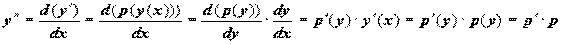 .
.
|
|
|
|
|
|
Аналогично, 
Также находятся следующие производные, и всегда k -ая производная y по x выражается через k-1 -ую производную p по y. В случае уравнения второго порядка  в результате таких преобразований получим
в результате таких преобразований получим 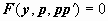 , т.е. уравнение первого порядка (в котором yвыступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1) этого уравнения решается уравнение
, т.е. уравнение первого порядка (в котором yвыступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C1) этого уравнения решается уравнение  , решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
, решение которого y = y(x, C1, C2) будет общим решением исходного уравнения.
 Примеры: 1. Задача Коши
Примеры: 1. Задача Коши  .
.
Переменная x явно в уравнение не входит, поэтому полагаем  ,
,  , тогда
, тогда  . Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений
. Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений  , поэтому рассматриваем два случая:
, поэтому рассматриваем два случая:
 1.
1.  ;
;
 2.
2.  Это - уравнение с разделяющимися переменными:
Это - уравнение с разделяющимися переменными:  . Получено уравнение
. Получено уравнение  , решаем его:
, решаем его: 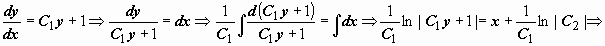
 . Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C2 = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из
. Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C2 = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из 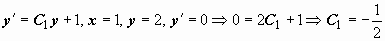 . Далее, из
. Далее, из  следует, что
следует, что  , т.е. C2 = 0. Частное решение -
, т.е. C2 = 0. Частное решение -  , т.е. y = 2.
, т.е. y = 2.
Пример 2. 
 Решение:
Решение: 

 . Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть
. Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть 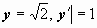 , то получим
, то получим  . Поэтому частное решение должно удовлетворять уравнению
. Поэтому частное решение должно удовлетворять уравнению  . Находим
. Находим 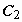 :
: 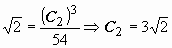 . Ответ: решение задачи Коши
. Ответ: решение задачи Коши 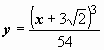 .
.
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
В этой статье поговорим о решении линейных однородных и неоднородных дифференциальных уравнений порядка выше второго с постоянными коэффициентами. Такие уравнения имеют вид  и
и  , где
, где  - действительные числа, а функция f(x) непрерывна на интервале интегрирования X.
- действительные числа, а функция f(x) непрерывна на интервале интегрирования X.
Сразу скажем, что аналитически решить такие уравнения далеко не всегда возможно и обычно используют приближенные методы. Однако в некоторых случаях возможно отыскать общее решение.
Сформулируем две теоремы, которые показывают, в каком виде искать общие решения ЛОДУ и ЛНДУ.
Общим решением y0 линейного однородного дифференциального уравнения 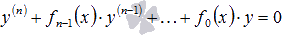 на интервале X с непрерывными коэффициентами
на интервале X с непрерывными коэффициентами  на X является линейная комбинация n линейно независимых частных решений ЛОДУ
на X является линейная комбинация n линейно независимых частных решений ЛОДУ  с произвольными постоянными коэффициентами
с произвольными постоянными коэффициентами  , то есть
, то есть  .
.
Общее решение y линейного неоднородного дифференциального уравнения  на интервале X с непрерывными на том же промежутке Xкоэффициентами
на интервале X с непрерывными на том же промежутке Xкоэффициентами  и функцией f(x) представляет собой сумму
и функцией f(x) представляет собой сумму 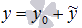 , где y0 - общее решение соответствующего ЛОДУ
, где y0 - общее решение соответствующего ЛОДУ 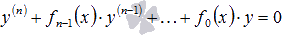 , а
, а 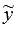 - какое-нибудь частное решение исходного ЛНДУ.
- какое-нибудь частное решение исходного ЛНДУ.
Таким образом, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами  ищем в виде
ищем в виде 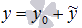 , где
, где 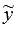 - какое-нибудь его частное решение, а
- какое-нибудь его частное решение, а  – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения  .
.
Сначала разберемся как находить  , а в конце покажем как определить
, а в конце покажем как определить 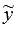 .
.
Уравнение  называется характеристическим уравнением линейного однородного дифференциального уравнения
называется характеристическим уравнением линейного однородного дифференциального уравнения  . Если мы найдем все n корней характеристического уравнения
. Если мы найдем все n корней характеристического уравнения  , то, исходя из их значений, можно определить n частных линейно независимых решений
, то, исходя из их значений, можно определить n частных линейно независимых решений  исходного ЛОДУ.
исходного ЛОДУ.
Перечислим все возможные варианты и разберем примеры на каждый из них:
1. если все решения характеристического уравнения  действительные и различные, то линейно независимые частные решения имеют вид
действительные и различные, то линейно независимые частные решения имеют вид

и
 ;
;
2. если все решения характеристического уравнения действительные и одинаковые  , то линейно независимые частные решения имеют вид
, то линейно независимые частные решения имеют вид

и

3. если решениями характеристического уравнения являются различные комплексно сопряженные пары  , n = 2m, то линейно независимые частные решения имеют вид
, n = 2m, то линейно независимые частные решения имеют вид

и
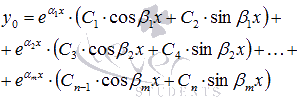
если решениями характеристического уравнения являются совпадающие комплексно сопряженные пары  , то линейно независимые частные решения имеют вид
, то линейно независимые частные решения имеют вид
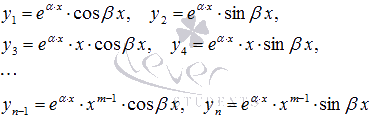
и

1. Пример.
Найдите общее решение линейного однородного дифференциального уравнения третьего порядка с постоянными коэффициентами 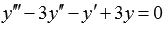 .
.
Решение.
Запишем характеристическое уравнение и найдем его корни, предварительно разложив многочлен в левой части равенства на множители способом группировки:
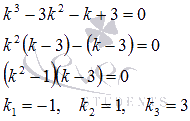
Все три корня действительные и различные, поэтому общее решение ЛОДУ имеет вид
 .
.
2. Пример.
Найдите общее решение дифференциального уравнения  .
.
Решение.
Характеристическое уравнение этого ЛОДУ четвертого порядка имеет вид  . Если обратиться к формуле бинома Ньютона, то характеристическое уравнение можно переписать в виде
. Если обратиться к формуле бинома Ньютона, то характеристическое уравнение можно переписать в виде  , откуда видно его четырехкратный корень k0 = 2. Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами есть
, откуда видно его четырехкратный корень k0 = 2. Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами есть
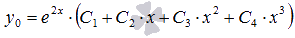 .
.
Дата добавления: 2018-02-15; просмотров: 675; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
