Признак Вейерштрасса равномерной сходимости ФР.
Т) Если дан ФР  и
и  (Cn≥0) – сходится, при этом ½Un(x)½≤Cn " x Î<a,b>, то ряд
(Cn≥0) – сходится, при этом ½Un(x)½≤Cn " x Î<a,b>, то ряд  – сходится равномерно на <a,b>
– сходится равномерно на <a,b>
Доказательство:
S(x)=Sn(x)+Rn(x)
Rn(x)=S(x)-Sn(x)

Частичная сумма остаток
½Rn(x)½=½Un+1(x)+Un+2(x)+…½≤Cn+1+Cn+2+…≤an<e " n>N(e) т.к.  – сходится
– сходится
½Rn(x)½<e " x Î <a,b> Þ ½Sn(x)-S(x)½<e " x Î <a,b>
Теорема о непрерывности суммы равномерно сходящегося ряда.
Теорема. Сумма ряда непрерывных функций, мажорируемого на некотором отрезке [о, Ь], есть функция, непрерывная на этом отрезке.
Доказательство.
U1(x)+U2 (x)+U3 (x) +… (1)
S(x)=Sn(x)+Rn(x)
Sn= U1(x)+…+Un (x)
Rn(x)= Un+1(x)+Un+2 (x)+…
Возьмем на отрезке [а, b] произвольное значение аргумента х и придадим ему такое приращение Dх, чтобы точка х+Dx лежала тоже на отрезке [a, b].
Введем обозначения:
DS=S(x+Dх)—S(х), DSn = Sn(х +D х)—Sn(х),
тогда
DS=DSn+Rn(x+Dх)-Rn(х),
откуда
|DS| ≤ | DSn | + | Rп(х+Dх) | + | Rn (x) |. (2)
Это неравенство справедливо для любого номера п.
Чтобы доказать непрерывность S(х), нужно показать, что при любом наперед заданном и как угодно малом e > 0 найдется число s > 0 такое, что при всех | Dx | < s будет | DS | < e.
Так как данный ряд (1) мажорируемый, то при любом наперед заданном e > 0 найдется такой номер N, что при всех п ≥ N, будет выполняться неравенство
| RN(x) | < e/3 (3)
при любом х из отрезка [a, b]. Значение х+Dх лежит на отрезке [а, b] и потому выполняется неравенство
| RN(x+Dx) | < e/3. (3')
|
|
|
Далее, при выбранном N частичная сумма SN (х) есть функция непрерывная (сумма конечного числа непрерывных функций) и, следовательно, можно подобрать такое положительное число s, что для всякого Dх, удовлетворяющего условию | Dx | < s, выполняется неравенство ,
| DS(x)| < e/3. (4)
На основании неравенств (2), (3), (3') и (4) получаем
| DS(x)| < e/3 + e/3 + e/3 = e
т. е.
| DS(x)| < e при | Dx | < s,
а это и означает, что S(х) является непрерывной функцией в точке х (и, следовательно, в любой точке отрезка [a, b]).
Замечание. Из доказанной теоремы следует, что если сумма ряда на каком-либо отрезке [а, b] разрывна, то ряд не мажорируем на этом отрезке.
T) (о почленном интегрировании)
Если ряд сходится равномерно в <a,b>, то  , где [a1, x] Ì <a,b>
, где [a1, x] Ì <a,b>

Доказательство.
S(x)=Sn(x)+Rn(x)


½  =
= 

<e (в силу равномерной сходимости)



e(b-a)≥  Þ
Þ 
e1
В итоге 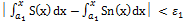 Þ
Þ



Т) (о почленном дифференцировании)
Пусть: 1) дан  (сходится " x Î <a,b>)
(сходится " x Î <a,b>)
2) Un(x) – непрерывно дифференцируемы в <a,b>, т.е. $ U’n(x) " x <a,b>
3)  – сходится равномерно в <a,b>
– сходится равномерно в <a,b>
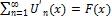 – непрерывная функция
– непрерывная функция
Тогда 
Доказательство: на теоремы о почленном интегрировании 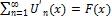 можно почленно интегрировать на [a1, x] Ì <a,b>
можно почленно интегрировать на [a1, x] Ì <a,b>
|
|
|

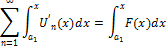



S(x)-S(a1)= 
(S(x)-S(a1))’x= 
S’(x)=F(x)
S’(x)=F(x)= 
Степенные ряды, обобщенные степенные ряды: осн. понятия и определения. Обл. сходимости степенного ряда. Доказать теор. Абеля для степ. ряда. Свойства рядов: а)непрерывность суммы степ. ряда; б)о почленном интегрировании; в)о почленном интегрировании.
ОСтепенным рядом наз-ся функциональный ряд вида 
Областью сходимости степ. Ряда явл. некоторый интервал, который, в частности, может выражаться в точку
Т АбеляПусть дан 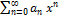 (1)
(1)
А)Если (1) сх-ся при  , то он сх-ся
, то он сх-ся  абсолютно
абсолютно
Б)Если (1) расх-ся при  , то он расх-ся
, то он расх-ся 
Д-во: А) Дано:  - сх-ся, т.е.
- сх-ся, т.е.  – сх-ся, т.е.
– сх-ся, т.е.  ограничена, т.е.
ограничена, т.е. 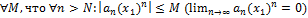
Тогда:  - сх-ся
- сх-ся  – сх-ся и притом абсолютно
– сх-ся и притом абсолютно
Б) Дано  – расх-ся. Пусть
– расх-ся. Пусть  . Предположим, что
. Предположим, что  – сх-ся (
– сх-ся (  , тогда по части (А)
, тогда по части (А)  должен сходиться,что противоречит условию. Теор. док.
должен сходиться,что противоречит условию. Теор. док.
Свойства рядов:
Т Сумма степ. Ряда – непрер-я ф-я в ОС, т.е. если 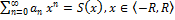 , то S(x)-непрер. в
, то S(x)-непрер. в 
ТСтеп. ряд в ОС моно почленно интегрировать и при этом 
ТСтеп. ряд можно дифференцировать в ОС и при этом : 1)  ; 2) OC:
; 2) OC: 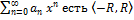
Вопрос
PU y(x)=  y(0)n/n!*xn xϵ<-R,R> (1)
y(0)n/n!*xn xϵ<-R,R> (1)
PT y(x)=  y(0)n/n!*(x-x0) xϵ<-R,R> (2)
y(0)n/n!*(x-x0) xϵ<-R,R> (2)
1. Вычисление значений функций y(x) x=x1. Раскладываем функцию в ряд Тейлора и Маклорена и вычисляем значение функции
|
|
|
2. Вычисление интегралов.  fn(x0)/n!(x-x0)n=
fn(x0)/n!(x-x0)n=  fn(x0)/n! (x-x0)ndx=
fn(x0)/n! (x-x0)ndx=  fn(x0)/n!
fn(x0)/n!  (x-x0)ndx=
(x-x0)ndx=
 f(x0)(x-x0)n+1/n!(n+1)
f(x0)(x-x0)n+1/n!(n+1)  [a,b]
[a,b]  <-R,R>
<-R,R>
3. ДУ. a) Линейные ДУ. y’’+p(x)y’+g(x)y=0 Пусть p(x)= 
q(x)=  ; y(x)=
; y(x)= 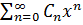 (3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении
(3) Подставим (3) в и находим коэффициенты Сn и находим из обращения в нуль коэффициентов при любой степени х в полученном выражении
б) Если p(x)= 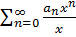 ; q(x)=
; q(x)=  Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs
Пусть a0,b0,b1 не равны, о оновр тогда решение уравнения (1) можно искать в виде обобщённого степенного ряда y(x)=xs  ; ρ(ρ-1)+a0ρ+b0=0 (6)
; ρ(ρ-1)+a0ρ+b0=0 (6)
a0=  ,b0=
,b0= 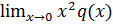
a) Если ρ1-ρ2- не целое. y1(x)=xρ1  ; y2(x)=xρ2
; y2(x)=xρ2 
y00=c1y1(x)+c2xy2(x) (!!!)
б) Если ρ1-ρ2- целое
2.1 Ряд Фурье. Пространство функции L2 [- 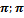 ]. Определение, св-ва.
]. Определение, св-ва.
Рассмотрим множество f(x) :  =
=  непрерывные на [-
непрерывные на [-  ]
]
Кусочные непрерывные [-  ], имеющие кон число точек разрыва 1го рода
], имеющие кон число точек разрыва 1го рода
Свойства функции:
1) Если f(x)  L2 , то С*f(x)
L2 , то С*f(x)  L2
L2
Доказательство:  =С2*
=С2*  <
< 
2) Если f1(x);f2(x)  L2 то f1(x)+f2(x)
L2 то f1(x)+f2(x)  L2
L2
Д-во: (f1(x)+f2(x))2  0
0
f12  f1f2+f22
f1f2+f22  => f12+f22>
=> f12+f22>  f1f2
f1f2
 =
= 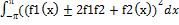 <
<  <2
<2 
Благодаря этим свойствам образуется линейное векторное пространство, которым можно показать, что L2 не имеет конечного базиса. Базис содержит бесконечное множество векторов
Можно ввести скалярное произведение:
{f(x),g(x)} = 
1) (g(x), f(x)) = 
(f(x),g(x)) =(g(x),f(x))
2) {f1(x)+f2(x),g(x)} =  =
= 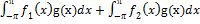
(  +
+  )*
)*  =
=  *
*  +
+  *
* 
3) { f(x), f(x)} = 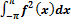
 0
0
|
|
|
4) (|f(x)|) = 
5) {|f(x)-g(x)|}= 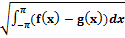
2(Ряды Фурье). Показать ортогональность функций 1, cosx, sinx, cos2x, sin2x,…,cosnx, sinnx,… на [-π,π].
{1, sinx, cosx, sin 2x, cos 2x, ... , sin nx, cos nx, ...}
1.  Поэтому
Поэтому 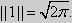
2. 
3. 
4. 


Если n=m, то 
5. 
при n ≠ m, n, m = 1, 2, 3, ... Если n = m, то 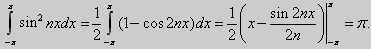
Значит, 
6. 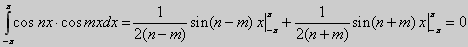
при n ≠ m, n, m = 1, 2, 3, ... Если n = m, то 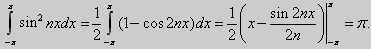
То есть 
Таким образом, доказано, что система на отрезке [ - π, + π] ортогональная.
Вопрос 3 фурье

5)Ряд Фурье для периодических функций с периодом T=2l
Пусть f(x) есть период. ф-я с T=2l,отличным от 2π. Разложим ее в ряд Фурье. Замена переменной:  /
/
Тогда ф-я 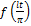 будет переод-й ф-й от t c T=2π. Ее можно разложить на
будет переод-й ф-й от t c T=2π. Ее можно разложить на 
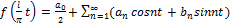 ,где
,где 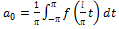 ,
, 
Возвратимся к старой переменной: 
Имеем: 
Ряд Фурье будет иметь вид: 
Дата добавления: 2018-02-15; просмотров: 539; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
