Достаточные признаки сходимости
Признак Даламбера
Если в ряде 
(an 
) 
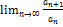=L
L<1-сходится
L>1 расходится
L=1 -??
Доказательство
a) L<1; 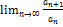=L
L<q<1
=q-L>0
< 
< 
= q-L
<q
Начиная с 
aN+1<q*aN
aN+2<q*aN+1<q2an
a1+a2+a3+…aN+aN+1+aN+2+… (4)
aN + q*aN+q2aN+q3aN+… (5)
начиная с номера 
члены ряда (1)<(2)
а ряд (2)-геометрическая прогрессия со знаменателем q>1
= 
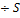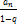- кон.число по теореме сравнения в форме неравенства
L>1; 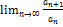=L члены с каждого номера члены ряда возрастают an+1>an, т.е. не выполняется НУС
а значит ряд расходится
в) L=1-???
Коши-Радикальный
Если в (an ), 
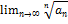=L, то
L<1-ряд сходится
L>1-ряд расходится
L=1-??
Доказательство
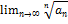=L 
=> | 
<
L<1
=q-L
-L< =q-L
<qn начиная с некоторого номера
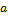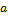n<qn
N<qN
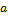N+1<qN+1
2 ряда
a1+a2+a3+…aN+aN+1+aN+2+… (6)
qN+qN+1+qN+2+… (7)
начиная с N члены (6)<(7) ряд (7) геом прогрессия 
q<1; = 
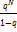- конечное число, тогда по признаку сравнения (6) сходится
Б) L>1 aN+1>aN; aN>1 т.е не выполняется НУС
В) L=1-??
Признак Коши-Интегральный
Рассмотрим ряд (an )
a(n) непрерывная функция на [n0; 
]
Если 
, - конечное число, то 
–сходится
Если =0, или , то 
– расходится
=A(n) 
= 
Вопрос 20.Если для последовательности {Sn,n≥1} частичных сумм существует конечны предел S, то ряд называется сходящимся, а число S-суммой данного ряда. Ряд называется расходящимся, если lim Sn (при n→0) не существует или бесконечен.
НУС Для того что бы ΣAn сходился, необходимо, что бы lim An(при n→0)=0
Если ряд сходится то остаток ряда тоже сходиться. Отбрасывание первых членов ряда не влияют на сходимость. Если ряд сходиться то остаток стремиться к нулю.
|
|
|
Т Знакоположительный ряд всегда имеет сумму: А) Если сумма ряда конечна, то ряд сходиться. Б) Если сумма бесконечна, то ряд разходится.
Абсолютная и условная сходимость Ряд ΣA (от 1 до ∞) называется абсолютно сходящимся, если ряд Σ‖A‖ также сходится.
Если ряд ΣAn (от 1 до ∞) сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд ΣА (от 1 до ∞) называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Знакочередующиеся ряды. Доказать теорему Лейбница.
= a1-a2+a3-a4+…-…+ 
+…
an≥0
Доказать теорему Лейбница
Если в (an≥0) выполняется 
=0, то
1. Ряд сходится
2. S>0
3. S<a1
Док-во:
S2n= a1-a2+a3-a4+…+a2n-1-a2n+…
a) S2n= (a1-a2)+(a3-a4)+…+(a2n-1-a2n)+…
≥0 ≥0 ≥0
S2n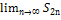≥0, 
≥0
б) S2n= a1-(a2-a3)-(a4-a5)-…-(a2n-2-a2n-1)- a2n…
S2n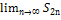≤ a1, ≤ a1
в) S2n+1= S2n+ a2n+1 0 НУС
= + 
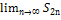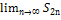= чтд.
Функциональные ряды.
О) ФР: 
(1) x Î<a,b> (1)
O) Если в (1) x=x0, то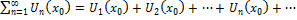 
(2) – числовой ряд
О) Если 
– (2) сходится, то говорят, что ФР (1) сходится в (.) x0
|
|
|
О) Если – (2) " x0 Î <a,b>, то говорят, что ФР (1) сходится на <a,b>
О) Если - (2) расходится, то ФР (1) расходится в (.) x0
О) - (2) сходится в (.) x0, если 
Частичная сумма сумма числового ряда
т.е. " e>0 $ N(e,x0): "(n>N) Þ ½Sn(x0)-S(x0)½<e
!!! N(e,x0) зависит и от e и от x0
Равномерная сходимость.
О) ФР (1) сходится равномерно на <a,b>, если " e>0 $ N(e): "(n>N) Þ ½Sn(x)-S(x)½<e " “x” Î <a,b> одновременно, где Sn(x)=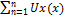 
– частичная сумма, S(x) – сумма ряда
S(x)=Sn(x)+Rn(x)
Rn(x)=Un+1(x)+Un+2(x)+… - остаток ряда
Дата добавления: 2018-02-15; просмотров: 360; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!