Завдання 1 Розрахувати приведений до поточного моменту розмір платежів.
Приклад роз’язання: Припустимо, що протягом визначеного періоду середньорічний темп приросту індексу акцій підприємств промисловості склав 10%; середня прибутковість дивідендів за той же період – 15%, інфляція – 20%.
Тоді реальна прибутковість інвестицій у промислові акції склала:
.
У майбутньому очікується, що середньорічні темпи росту промислового виробництва (π) збільшаться на 1% у реальному вираженні, а темп інфляції (a)знизиться до 15% річних. Тоді відповідно до формули Фішера 
, необхідна прибутковість акцій повинна становити r = 0,0417 + 0,01 + 0,15 + (0,0417 + 0,01) · 0,15 = 20,95% річних.
Модель із постійними дивідендами
Відповідно до даної моделі передбачається, що розмір дивідендів не змінюється в часі. Якщо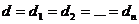 
, тоді приведена вартість дивідендів, а, отже, і ринкова ціна акцій буде дорівнювати:
. (3.5)
У тому випадку, коли термін володіння акцією не обмежений деякими тимчасовими рамками ( 
), вартість акції дорівнює розміру дивідендів, виплачуваних по акції, поділену на ставку необхідної прибутковості. По суті, процедура дисконтування дивідендів (3.5) вироджується в процедуру прямої капіталізації дивідендів:
. (3.6)
При цьому, внутрішня норма прибутковості визначається як:
, (3.7)
|
|
|
де Р - поточна ринкова ціна акції.
Завдання 2 Необхідно визначити цінові параметри акції.
Приклад роз’язання: На фондовому ринку продається акція, за яку продавець просить ціну в Р = 50 грн. Прогнозований рівень дивідендів – d = 15 грн/рік. Прибутковість альтернативного розміщення капіталу r = 25% річних. Необхідно визначити цінові параметри акції.
За формулою (3.6) визначаємо капіталізовану вартість акції V = 15/0,25 = 60 грн. За формулою (3.7) внутрішня норма прибутковості 
= 15/50 = 30%. Оскільки P < V а >r – акція є недооціненою.
Моделі з виплатами дивідендів , що змінюються в часі
Сценарії з постійними дивідендами на практиці зустрічаються досить рідко. Умовам практичної діяльності акціонерних товариств відповідають сценарії з виплатами дивідендів, що змінюються в часі. При цьому розрізняють:
- сценарії з постійним темпом приросту дивідендів;
- сценарії з перемінними темпами приросту дивідендів.
Модель із постійним темпом приросту дивідендів
Якщо виплати дивідендів на одну акцію в базовому році (періоді) складають d0, а в наступних передбачається приріст виплат на визначений розмір g, то дисконтований розмір дивідендів, а, отже, і вартість акції складе:
|
|
|
(3.8)
або
. (3.9)
У тому випадку, коли термін володіння акцією не обмежений деякими тимчасовими рамками ( ), вартість акції дорівнює розміру дивідендів, виплачуваних по акції, поділеному на різницю між ставкою необхідної прибутковості і темпом приросту виплат дивідендів. По суті, як і у випадку моделі з постійною виплатою дивідендів, процедура дисконтувания
, (3.10)
вироджується в процедуру прямої капіталізації:
. (3.11)
Формула (10) має сенс, якщо r > g.
Внутрішня норма прибутковості визначається за формулою:
. (3.12)
Дата добавления: 2018-02-15; просмотров: 673; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!