Максвеллдан алынды. Примерно келеді деп ойлайм
Nbsp; 1. Электромагнитті индукция құбылыстары Электромагнитті индукцияның негзгі заңдары. Ленц ережесі.(1831 ж. ағылшын ғалымы М. Фарадей) Тұйық контурмен шектелген аудан арқылы өтетін магнит индукциясының ағыны өзгергенде контурда электр тогы пайда болатын құбылыс электрмагниттік индукция құбылысы деп аталады. Ал пайда болган ток индукциялық ток деп аталады. Электрмагниттік индукция заңы алынды: тұйық контурда пайда болатын электрмагниттік индукцияның ЭҚК-і сан жағынан осы контурмен шектелген бет арқылы өтетін магнит ағынының уақытқа байланысты өзгеру жылдамдығына тең және таңбасы бойынша қарама-қарсы: Энергияны сақталу заңыра сәйкес ток көзінің жұмысы dt(epsilonIdt) уақыт ішінде джоуль жылуына(I^2Rdt) және магниттік өрісте (IdФ) өткізгішті орын ауыстыру бойынша жұмысқа жұмсалады epsilonIdt=I^2Rdt+IdФ.Осыдан фарадей заңы шығады I=(epsilon-(dФ/dt))/R dФ/dt=epsilon. Индукциялық токтың бағыты Ленц ережесі бойынша анықталады: индукциялық токтың тудыратын магнит өрісі индукциялық токты тудырған магнит өрісінің өзгерісіне кедергі келетіндей болып бағытталады. Екінші текті индукциялық құбылыстың мысалы ретінде біртекті магнит өрісінде магнит индукция векторына перпендикуляр жылдамдықпен қозғалатын тогы жоқ, ұзындығы өткізгіш алынады. Өткізгішпен бірге қозғалған әрбір электронға магнит өрісі тарапынан Лоренц күші әсер етеді. Нәтижесінде өткізгіштің ұштарында потенциалдар айырмасы пайда болады U=|Bv|l . 2 Ядроның байланыс энергиясы. Ядроның бөліну реакциясы. Энергия көздерінің мәселелері. Дәл өлшеулер бойынша ядроның массасы ондағы нуклондардың массаларының қосындысынан әрқашанда кіші болатыны шығады . Ядродағы нуклондардың массаларының қосындысынан оның массасының айырымы массалық ақау деп аталады. Массалық ақау ядродағы нуклондардың байланыс энергиясын сипаттайды. Байланыс энергиясы – ядроның оны құрайтын нуклондарға ыдыратуға кететін минимал энергия. Байланыс энергиясы ядроның беріктігін сипаттайтын негізгі шамалардың бірі. Ядроның байланыс энергиясын біле отырып, кез келген ыдырау және ядролардың өзара түрлену процесстері үшін энергетикалық шығыстарды есептеуге болады . (15.3) Практикалық есептеулерде төмендегі формуланы қолдану ыңғайлы , мұндағы – атом массасы; – сутегі атомының массасы. Байланыс энерсиясының А толық нуклондар санына қатынасы меншікті байланыс энергиясы деп аталады. Ядроның бөлінуі, атом ядросының бөлінуі – ауыр атом ядроларының өздігінен не басқа бір бөлшектердің әсерінен бірнеше бөлшекке (көбінесе 2 бөлшекке, сиректеу 3 және 4 бөлшекке) бөлінуі. Ядроның нейтрондар арқылы бөлінуінің практикалық маңызы бар. Атом ядросы протондар, дейтрондар-g, кванттар, т.б. арқылы да бөлінеді. ядро бөлінуінің алғашқы теориясын 1939 ж. Я.И. Френкель (КСРО), сондай-ақ Н. Бор және Дж. Уилер (АҚШ) жасады. Атом ядросының бөлінуі кезінде жарықшақтармен қатар нейтрондар және γ-кванттар да бөлініп шығады. Әрбір ядро бөлінгенде 200 МэВ-қа жуық энергия бөленіді. Ядроның бөлінуі кезінде бөлініп шығатын нейтрондарды шапшаң және баяу нейтрондар деп аталатын екі топқа бөлуге болады. Тізбекті реакция жүру үшін әрбір нейтронның ядроны бөлуі шарт емес. Тек ядроға тізбекті реакция өту үшін қажетті мөлшердегі нейтрондардың саны түссе болғаны. Ядролық энергияны алуда ,ядроларының бөлінуінің ерекше маңызы бар. Висмут, қорғасын, мыс, күміс, ядроларының да бөлінетіндігі анықталды. Алайда бұдан гөрі жеңіл ядролар өте сирек бөлінеді. 3 Өздік және өзара индукця құбылыстары Индуктивтілік. Ұзын соленоид индуктивтілігі. Егер электр тізбегінде уақыт бойынша өзгеретін ток жүрсе, онда осы токтың магнит өрісі де өзгереді, олай болса, магнит ағынының өзгерісі индукцияның ЭҚК-н тудырады. Бұл құбылыс өздік индукция деп аталады. Өздік индукцияның ЭҚК-і Фарадей заңынан анықталады. Ферромагнетик болмаған кезде контур арқылы өтетін магнит ағыны I ток күшіне пропорционал , L - контурдың индуктивтілігі деп аталатын коэффициент, ХБ жүйесінде өлшем бірлігі - генри (Гн).Контурдың индуктивтілігі L контурдың пішіні мен өлшемдеріне, сондай-ақ қоршаған ортаның магниттік қасиеттеріне тәуелді. Егер ферромагниттік орта болса, онда контурдың индуктивтілігі ток күшінің өзгерісіне байланысты өзгереді, ағын ілінісуі ψ мен ток күшінің арасындағы пропорционалдық қатынас бұзылады (1.3). Ұзын соленоидтың индуктивтілігінің формуласын магнит өрісінің индукциясы , ағын ілінісуі , бір орам арқылы өтетін магнит ағыны үшін жазылған қатынастарды пайдаланып, анықтауғаболады: мұндағы - бірлік ұзындыққа келетін орамдар саны; - соленоидтың көлемі Ток өзгергенде өздік индукцияның ЭҚК-і пайда болады Минус таңбасы әрқашан ток күшінің өзгерісіне кедергі жасайтындай етіп бағытталады, токты өзгеріссіз сақтауға ұмтылады, яғни токқа қарама-қарсы әсер етеді. Өздік индукция құбылыстарында ток инерттілікке ие болады, себебі бұл жерде индукция әсерінің магнит ағынын тұрақты етіп ұстауға ұмтылуы айтылып тұр, ал индуктивтілік ток күшінің өзгерісіне қатысты контурдың инерттілік мөлшері болып табылады. . Өздік индукцияның пайда болуы тізбекті ток көзіне қосу және ажырату кезінде байқалады. Контурдағы ток күшінің өзгерісі пайда болуына алып келеді, нәтижесінде контурда өздік индукцияның экстратоктары деп аталатын қосымша токтар пайда болады. Тізбекті қосқанда токтың орнығуы мен тізбекті ажыратқанда токтың кемуі лезде емес, біртіндеп болады. Тізбектің индуктивтілігі жоғары болған сайын, бұл эффектілер соғұрлым баяу болады. Өзара индукция құбылысы Әрбір контурдағы ЭҚК-і басқа контурдағы токтың тудыратын магнит ағынының өзгерісі есебінен пайда болады. Бұл құбылыс өзара индукция құбылысы деп аталады. Бір-біріне жақын орналасқан екі қозғалмайтын контурларды қарастырайық Егер 1 контурда ток жүрсе, ол екінші контур арқылы өтетін толық магнит ағынын тудырады онда осы сияқты екінші контурда ток жүрсе, ол бірінші контур арқылы өтетін толық магнит ағынын тудырады . және коэффициенттері – бірінші контурдың екінші контурға қатысты және сәйкесінше екінші контурдың бірінші контурға қатысты өзара индуктивтілігі деп аталады. Сызықты орталарда, мысалы ферромагнетиктер жоқ кезде, . Өзара индуктивтілік магниттік байланысқан контурлардың геометриялық өлшемдеріне, олардың орналасуына және ортаның магниттік қасиеттеріне тәуелді. Электрмагниттік индукция заңына сәйкес 1 және 2 контурларда пайда болатын ЭҚК-тері: , Токтар мен кернеулерді түрлендіруші құрылғылар – трансформаторлардың жұмыс істеу принципі электрмагниттік индукция құбылысына негізделген. Токтың магнит энергиясы. Магнит өрісінің энергиясының көлемдік тығыздығы. Магнит өрісінің энергиясы Егер индуктивтілігі контурда ток жүрсе, онда тізбекті ажырату мезетінде жойылып кететін магнит өрісінің энергиясы есебінен жұмыс атқаратын индукциялық ток пайда болады. Энергияның сақталу және айналу заңына сәйкес магнит өрісінің энергиясы негізінен электр өрісінің энергиясына айналады, осының нәтижесінде өткізгіш қызады. Жұмыс қатынасымен анықталады. аламыз. Магнит өрісінің энергиясының кемуі токтың жқмысына тең, сондықтан . Сонымен, ток өтетін индуктивтілігі контур энергияға ие болады. Энергияны ұзын соленоидтың және өрнектерін қолданып, магнит индукциясы арқылы өрнектеуге болады. Нәтижесінде көлемдегі біртекті өрістің энергиясының формуласын аламыз Магниттік энергия магнит өрісі бар кеңістікте жинақталады және осы көлемде көлемдік тығыздықпен таралады , мұндағы - энергияның көлемдік тығыздығы барлық жерде бірдей деп есептелген шектегі магнит өрісінің аз аймағының көлемі. көлемдегі магнит өрісінің энергиясы 4 Радиоактивтік ыдырау заңы.Жартылай ыдырау периоды. Радиоактивтік ыдырау түрлері. Радиоактивті құбылыс-атомдардың өздігінен сәуле шығаруы. Радиоактивті сәуле шығаратын заттар қасиеті радиоактивтілік деп аталады.Радиоактивтік элементтердің (уран,торий,радий т.б.) атомдары α,β,ϒ-сәулелерін шығара отырып, басқа бір элемент атомына айналады. Орнықсыз ядролардың белгілі уақыт аралығында орнықты күйге келіп үлгеретін шамасын көрсететін заңдылықты радиоактивтік заңдылықты радиоактивті ыдырау заңы атайды. Егер радиоактивтік ядроның алғашқы саны N0 болса, онда dt уақыт ішінде ыдырап үлгерген ядроның саны dN=-𝜆Ndt, мұндағы 𝜆-ыдырау тұрақтысы. , бұдан N= N0 . Бұл радиоактивті ыдырау заңы. Радиоактивті ядролардың жартысы ыдырап үлгеретін уақытты жартылай ыдырау периоды деп атайды. N= N0 , бұдан ln2=𝜆t, T= = .радиоактивті ядроның орташа өмір сүру уақыты ыдырау тұрақтысына кері шама. Радиоактивті ядроның активтігі A= . Ығысу ережесі: α-ыдырау үшін; β-ыдырау үшін; α-бөлшек гелий ядросы, ыдырау формуласы β-бөлшек электрондар ағыны, ыдырау формуласы . Бұдан басқа екі ыдырау түрі бар: p+ →n+ . ϒ-бөлшек – электромагниттік толқын. 5. Электромагниттік индукция құбылысының максвелдік және фарадейлік тұжырымдаулары. Құйынды электр өрісі. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы. Құйынды электр өрісі Электрмагниттік индукция құбылысын оқып-үйрену кезінде айнымалы магнит өрісінде тыныштықта тұрған контурда индукциялық ток пайда болатыны байқалған. Оның пайда болу себебі бөгде күштердің әсері. Бұл күштердің табиғаты электростатикалық, магниттік емес және жылулық немесе химиялық процесстермен де байланысты емес. Максвелл магнит өрісінің кез келген өзгерісі қоршаған кеңістікте индукцияланған электр өрісін тудырады, бұл контурдағы индукциялық токтың туындау себебі болып саналады деген болжам айтты. Электрстатикалық өрістен ерекшелігі индуцияланған электр өрісі потенциалды емес құйынды электр өрісі болып табылады, себебі осы өрісте бірлік оң зарядты тұйық контур бойымен орын ауыстырғанда атқарылған жұмыс нөлге тең емес, ол индукцияның ЭҚК-не тең ,мұндағы - айнымалы магнит өрісімен индукцияланған электр өрісінің кернеулігі. Электрмагниттік индукция заңынан Жалпы жағдайда электр өрісі электрстатикалық өріс және уақыт бойынша өзгеретін магнит өрісінің тудыратын өрісінің қосындысынан тұрады. Себебі, электрстатикалық өрістің циркуяциясы нөлге тең, теңдеуді өрісі осы екі өрістің векторлық қосындысынан тұратын жалпы өріс үшін келесі түрде жазуға болады . Максвелдің бірінші теңдеуі (2.3) электромагниттік өріске ойша енгізілген кез-келген қозғалмайтын тұйық контур бойынша алынған векторының циркуляциясы теріс таңбамен алынған беттен өтетін магнит ағынының өзгеру жылдамдығына тең. Бұдан Максвелл теориясының бірінші тұжырымы: магнит өрісінің кез-келген өзгерісі құйынды электр өрісін тудырады. Ығысу тогыМаксвелл айнымалы электр өрісі электр тогы секілді магнит өрісінің көзі болады деп болжай келе, толық ток заңын толықтырды1. Айнымалы электр өрісінің «магниттік әсерінің» сандық түрде сипаттау үшін ығысу тогы деген ұғым енгізілді. Тұрақты ток тізбегінде конденсатор үзіліс болып табылады, ал айнымалы токтың мұндай тізбекте өтетіндігі белгілі. Тізбектің барлық тізбектей жалғанған элементерінде де өткізгіштік квазистационар ток күші бірдей болады. Конденсаторда электрондардыңқозғалысымен байланысты өткізгіштік токтың болуы мүмкін емес, себебі конденсатор астарларының арасы диэлектрикпен толтырылған. Бұдан шығатын қорытынды, конденсаторда өткізгіштік токты тұйықтайтын қандай да бір процесс өтеді, бұл – ығысу тогы. Айнымалы ток тізбегінде (2.1 суретті қара) конденсатор астарлары арасында кернеулігі электр өрісі бар. Бұл формулада - астардағы зарядтың беттік тығыздығы, - астарлар арасындағы заттың диэлектрік өтімділігі.Заряды және пластиналардың ауданы конденсатор астарлары арасындағы электр ығысуы . Тізбектегі ток күші , бұдан , яғни конденсатор астарлары арасындағы электр ығысуының өзгеру жылдамдығы тізбектегі токты тұйықтайтын процесс болып табылады. Онда астарлар арасындағы кеңістіктегі ығысу тогының тығыздығы Максвелдің теориясына сәйкес (екінші тұжырымы), ығысу тогы өткізгіштік ток сияқты құйынды магнит өрісінің көзі болып табылады (2.1 суретті қара). Максвелдің екінші теңдеуін мына түрде жазуға болады , мұндағы - толық ток тығыздығы. электромагниттік өріске ойша енгізілген кез-келген қозғалмайтын тұйық контур бойынша алынған магнит өрісінің кернеулік векторының циркуляциясы беттен өтетін өткізгіштік және ығысу токтарының алгебралық қосындысына тең болатынын көрсетеді. Максвелл теңдеулерінің жүйесі Максвелл теңдеулерінің жүйесі 2.1 кестеде көрсетілген. Интегралдық түрі Дифференциалдық түрі 1. 2. 3. 4. 5. 6. 7. . Өзгеретін электр және пайда болған магнит өрістері арасындағы сандық қатынасты орнатуда Максвелл ығысу тоғы деп аталатынды енгізді. Максвелл идеясы бойынша айнымалы магнит өрісі әрқашанда өзін тудыратын электр өрісімен байланысты, ал өз кезегінде айнымалы электр өрісі өзін туғызған магнит өрісімен байланысты. Осы екеуі біртұтас электромагниттік өріс құрайды. 6.Атом ядросы. Атом ядросының құрылысы және негізгі қасиеттері. Ядролық күштер.Атом ядросы он зарядталган протоннан жане теріс заряды жок нейтроннан турады.Бұл бөлшектерді нуклондар деп атайды.Протоннын массасы mр=938,26МэВ.Спині s=1/2.Нейтроннын массасы mn=939.26МэВ.Спині s=1/2.Ядролық бөлшектің массасы массалық атомдық бірлігімен (м.а.б.)өлшенеді.1м.а.б. =1,66*10-27кг.Мұндағы протондар саны атом қабықшасындағы электрондар санына тең.Заряды +ze.Массалық саны A=z+N мұндағыN-нейтрондар саны.егер атом ядросының зарядтар саны бірдей, ал массалар саны әртүрлі болса,ядролар изотоптар деп аталады.Керісінше массалар саны бірдей болып,зарядтар саны әр түрлі болса изобаралар деп аталады.Нейтрондары бірдей болса изотоптар қатарын түзейді. Z пен А бірдей,бірақ жартылай ыдырау периодтары әр түрлі ядроларды изомерлік ядролар деп атайды.Ядро радиусы шамамен 10-15м.Ядролық бөлшектердің массалық санына тәуелді R=(1,5*10-15м)А1/3.Орташа тығыздығы ρ=1017кг/м3.Ядролық спині нуклондар спинінің қосындыларынан тұрады.Егер нуклондар саны А тақ болса ядро спині жарты бүтін,ал жұп(немесе нөл) болса нөлнемесе бүтін болады. Атом ядросындагы нуклондар нуклондар арасындагы тартылыс кушін ядролык куш деп атайды.олардың мынандай қасиеттері болады:1)Ядролық күштердің әсер ету ара қашықтығы шамамен r=10-15м.2)Бұл күштер қанығу қасиетіне ие болады.Бір нуклон белгілі нуклондармен ғана әсерлеседі.3)Ядролық күш нуклондардың зарядына байланысты емес.4)Бұл күштер табиғатта кездесетін күштердің ең қуаттысы,мысалы электромагниттік күштерден 100есе артық.5)Ядролық күштер центрлік күштер қатарына жатпайды.Ядролық күштер,нуклондардың спиндерінің бағытына тәуелді. 7. Электр тізбегін тұйықтау және ажырату экстратоктары. Өздік индукцияның пайда болуы тізбекті ток көзіне қосу және ажырату кезінде байқалады. Контурдағы ток күшінің өзгерісі пайда болуына алып келеді, нәтижесінде контурда өздік индукцияның экстратоктары деп аталатын қосымша токтар пайда болады. Тізбекті қосқанда токтың орнығуы мен тізбекті ажыратқанда токтың кемуі лезде емес, біртіндеп болады. Тізбектің индуктивтілігі жоғары болған сайын, бұл эффектілер соғұрлым баяу болады. Тұрақты кедергісі және индуктивтілігі тұйық тізбекте ток күшінің өзгеру заңдары осы тізбекті тұрақты ЭҚК ток көзіне қосу кезінде . және оны ажыратқанда .өрнектері арқылы жазылады. Бірінші қосынды ажырату экстратоктарына, екіншісі – тұйықтау экстратоктарына қатысты жазылған. суретте уақытқа тәуелділік графиктері келтірілген: 1 қисық – тізбекті ажырату кезіндегі ток күшінің кемуі 2 қисық – оны тұйықтаған кездегі ток күшінің артуы, орнығатын токты береді ( кезде). Токтың өзгеру жылдамдығы (кему немесе орнығу) тізбектің тұрақты уақыты немесе релаксация уақыты деп аталатын және уақыт өлшемімен есептелетін сурет тұрақты шамамен сипатталады. 8 Элементар бөлшектер. Фундаментальды әсерлеу. Элементар бөлшектер дег барлық алғашқы материяны құрайтын,әрі қарай бөлінбейтін бөлшектер.Барлық Э. б бір біріне түрленеді ж.е бұл өзара түрлену олардың өмір сүруінің басты шарты болып табылады. Э. б физикасының дамуы космостық сәулелердің ашылуымен байланысты.Э.бді массасына қарай фотондар , лептондар(жеңіл бөлшектер),мезондар(орташа бөл.),бариондар(ауыр б)Негізінен орнықты(40қа жуық саны) ж.е орнықсыз(200) болып бөлінеді.Спиндік санына байланысты а)егер s=+-1/2тең болса, онда бұл бөлшектер Паули принципіне негізделіп фермиондар д.а.б)егер s=+-1,+-2 болса, онда бозондар д.а Өз құрылымы мен құрамы болмайтын бөлшекті элементар бөлшек дейміз.барлық элементар бөлшектер бір-біріне түрленеді және бөлшектердің антибөлшектері болады.Бөлшектер өздерінің антибөлшектерімен әсерлескенде аннигилляция процесі жүреді,нәтижесінде олар басқа бөлшекке немесе фотонға айналады.Элементар бөлшектер космостық сәулелерден және үдеткіштер қондырғысы арқылы алынады.Элементар бөлшектер 4 топқабөлінеді:фотондар,лептондар,мезондар,бариондар. Бесінші ретінде бариондар қарастырылады. Бұл бөлшектер гравитациялық тартылыс әсерлесуінде қатысады. Бариондар мен мезондарды адрондар дейді.Элементар бөлшектер төрт әсерлесу күштерінде қатысады:күшті(ядролық), электромагниттік,әлсіз және гравитациялық күштер. Бір кездері молекулаларды, одан кейін атомдарды дүниенің бөлінбейтін кірпіші, яғни элементар бөлшегі деп айтқан болатын. Ал қазір элементар бөлшектер қатарында 400-ден аса бөлшектер бар. Фундамента́льные взаимоде́йствия — качественно различающиеся типы взаимодействияэлементарных частиц и составленных из них тел. Экспериментальная проверка Стандартной Модели заключается в обнаружении предсказанных ею частиц и их свойств. В настоящий момент открыты все элементарные частицы Стандартной Модели.Таким образом, в настоящее время фундаментальные взаимодействия описываются двумя общепринятыми теориями: общей теорией относительности (Cалыстр теориясы Салыстырмалықтың жалпы теориясы — кеңістік уақыт және тартылыс қасиеттерін біріктіретін физикалық теория E=mc2) и Стандартной Моделью. Их объединения пока достичь не удалось из-за трудностей создания квантовой теории гравитации. Для дальнейшего объединения фундаментальных взаимодействий используются различные подходы: теории струн, петлевая квантовая гравитация, а также М-теория. Станда́ртная моде́ль — теоретическая конструкция в физике элементарных частиц, описывающая электромагнитное,слабое и сильное взаимодействие всех элементарных частиц 9. Гармоникалық тербелістердің жалпы сипаттамалары. Табиғаттағы кез келген тербелістерді түсіндірудегі ұқсастық. Тербелістер-белгілі бір дәрежеде уақыт бойынша қайталанып отыратын процесстер. . Егер тербелiстер бiрдей уақыт аралығында қайталанатын болса, онда ондай тербелiстердi периодты тербелiстер деп атайды. Тербелiстiң қайталану уақытын тербелiс периоды деп атап, Т әрiпiмен белгiлейдi. Тербелiстiң νжиiлiгi деп бiрлiк уақыт мезетiнде жасалатын толық тербелiстердiң санын айтады, яғни . Ал тербелiстiң ω, циклдiк жиiлiгi ретiнде 2π уақыт бiрлiгiндегi жасалынатын тербелiстердiң саны алынады, яғни ω=2πν=2π/T, бұдан T=2π/ω. Тербелiс периодының өлшем бiрлiгi 1 секунд ( 1 с ), ал жиiлiктiң бiрлiгi ретiнде 1 с уақыт аралығында 1 тербелiс жасайтын тербелiстiң жиiлiгi алынған. Оны 1 Герц ( 1 Гц ) деп атайды. Периодты тербелiстiң қарапайым мысалы гармоникалық тербелiстер. Гармоникалық тербелістер-физикалық шамасы уақыт өтісімен синусоидалы немесе косинусоидалы заңдылықтар бойынша өзгеріп тұратын тербелістер. Тербеліп тұрған нүктенің ауытқуына пропорционал және осы ауытқуға қарама қарсы бағытталған күштер әсерінен туындайтын тербелістер гармоникалық болып табылады. x(t)=Asin(ωt+φ) немесе x(t)=Acos(ωt+φ), мұндағы x- уақыттың t моментіндегі тербеліп тұрған нүктенің тепе теңдік қалпынан ауытқуы; A- тербеліс амплитудасы – тербеліп тұрған нүктенің тепе теңдік жағдайынан максимал ауытқуын көрсететін шама; ω- циклдік жиілік, 2π секунд ішіндегі болатын толық тербелістердің санын көрсететін шама; (ωt+φ) - толық тербеліс фазасы, φ- бастапқы тербеліс фазасы Гармоникалық тербелістердің жалпы дифференциалдық түрі 2 түрі болады: Еркін тербелістер жүйе тепе теңдік жағдайынан шығарылған кездегі жүйедегі ішкі күштердің әсерінен болады. Еркін тербелістер гармоникалық болуы үшін тербелмелі жүйенің сызықты болуы керек. Еріксіз тербелістер сыртқы периодты күштер әсерінен болып тұрады. Олар гармоникалық болуы үшін тербелмелі жүйенің сызықты болуы, ал сыртқы күштер өздері уақыт өткен сайын гармоникалық түрде өзгеріп тұруы қажет. 10. Металдар және жартылай өткізгіштердегі байланыс құбылысы (Зеебек, Пельтье құбылыстары). Элетронды-кемтіктік байланыс ( p-n ауысу) Жартылай өткізгіштер — өзінің электрлік қасиеті жағынан өткізгіштер мен диэлектриктердің (мысалы, германий, кремний) арасынан орын алатын элементтер. Жартылай өткізгіштердің ерекшеліктері. Жартылай өткізгіштердің кәдімгі температурадағы электрөткізгіштігі металдардың электрөткізгішітігі мен салыстырғанда аз. Өте төмен температурада олар диэлектриктерге ұқсайды. Жартылай өткізгіштердің электрөткізгіштігі температура мен жарық әсерінен қатты өзгереді, яғни температура артып және жартылай өткізгіш неғұрлым қатты жарықталынса, оның электрөткізгіштігі де соғұрлым жоғары болады. Жартылай өткізгіштердің электрөткізгіштігі оның құрамына өте аз шамада қоспалар енгізу жолымен басқарылады. Зеебек эффектісі –екі түрлі температурадағы жартылай өт-ді қосқанда электр тоғы п.б. Пельте эф- әр түрлі екі өт-тен ток өткізетін болсақ онда джоульдік жылудан басқа қосымша жылу бөлінеді осы құбылыс. Электронды-Кемтіктік Ауысу, p–n-ауысу – монокристалл жартылай өткізгіштерге легирлеуіш қоспа (қ. Легирлеуіш элементтер) араластырғанда қоспалық электрондық өткізгіштердің (n-типтес) қоспалық кемтіктік өткізгіштік (p-типтес) пайда болатын аймақ (облыс). Жартылай өткізгіштердің p-немесе n-аймақтарында көлемдік электр зарядтары түзіледі. Осы электр зарядтарының электр өрісі, p-не n-аймақтары арқылы негізгі ток тасушылардың өтуіне (яғни өткізгіштік электрондардың n-аймағынан p-аймағына қарай, ал кемтіктердің кері бағытта өтуіне) кедергі жасайды. Сондықтан сол шекарада негізгі ток тасушылар үшін жапқыш қабат дейтін қабат түзіледі. Сыртқы электр өрісінде Э.-к. а. бір жақты (вентильді) өткізгіштік қасиетке ие болады (яғни ол p-аймағынан n-аймағына қарай жүретін токты өткізеді де, ал кері бағытта жүретін токты іс жүзінде өткізбейді). Э.-к. а. әр түрлі жартылай өткізгіштік приборларда (мыс., түзеткіш диодта, транзисторларда, т.б.) кеңінен қолданылады 11. Гармоникалық механикалық тебелістердің дифференциалды теңдеуі. Гармоникалық осцилляторлар.Физикалық маятник. Гармоникалық тербелістер-физикалық шамасы уақыт өтісімен синусоидалы немесе косинусоидалы заңдылықтар бойынша өзгеріп тұратын тербелістер. Тербеліп тұрған нүктенің ауытқуына пропорционал және осы ауытқуға қарама қарсы бағытталған күштер әсерінен туындайтын тербелістер гармоникалық болып табылады.Гармоникалық тербелістердің жалпы дифференциалдық түрі Гармоникалық осциляторлардегеніміз – екінші теңдеумен сипатталатын тербеліс жасайтын жүйе. Гарм осцилятор мысал ретінде: математикалық маятник, физикалық маятник, пружиналық маятник түрлерін жатқызуға болады. Физикалық маятник – оның инерция центріне дәл келмейтін қозғалмайтын нүкте маңында тербеліс жасайтын қатты дене. Т= 2П/ w, W= , T=2П , lкел= , T=2П 12. Жүйенің химиялық потенциалы (Ферми деңгейі). Металдардағы электронды өткізгіштік. Металдардың электр өткізгіштігі. Асқын өткізгіштік. Асқын өткізгіштікті ғылым мен техникада қолдану. Ферми деңгейі — жартылай бүтін спины 6aр бөлшектер (фермиондар) жүйесінің абсолют нөл температурада бос және толтырылған энергетикалық деңгейлерін бөліп тұратын энергияның мәні SF (Ферми энергиясы). Фл түсінігі шалаөткізгіштердің өткізгіштігін түсіндіретін аймақтық теориялар қолданылады. Өткізгіштер– электр тогын төмен) заттарsжақсы өткізетін, электр өткізгіштігі жоғары (меншікті кедергісі r=1/ Өткізгіштерге металдар, электролиттер және плазма жатады. Металдарда электр зарядын тасымалдаушылар – квазиеркін электрондар, электролиттерде – оң және теріс иондар, плазмада – еркін электрондар мен иондар.Асқын өткізгіштік [1] — кейбір өткізгіштерді белгілі бір алмағайып температураға (Та) дейін суыту кезінде олардың электрлік кедергісінің секірмелі түрде кенет нөлге дейін төмендеу құбылысы. Асқын өткізгіштік практикада кеңінен пайдаланылады. 20 ғасырдың соңында керамикалық материалдардың жоғары температурадағы (77-100 К) асқын өткізгіштігін зерттеу бағыты қарқынды дамуда. Ал Қазақстанда Асқын өткізгіштікті зерттеу ҚР ҒА-ның Ядр. физ. ин-тында (ҚР ҒА-ның корр. мүшесі Ә.Қ. Жетбаевтың жетекшілігімен) жүргізілуде. 13.Гармоникалық электр тебелістерінің дифференциалды теңдеуі. Гармоникалық электр тербелістерінің энергиясы. Тербелмелі контур. Гармоникалық тербелістердің жалпы дифференциалдық түрі Тербелмелі контур (орыс. Колебательный контур) — сыйымдылығы С конденстордан және индуктивтілігі L катушкадан тұратын, сондай-ақ Ω0= 1/√( LC )периодты электр тербелісін туғызатын тұйық контур. 14. Қатты денелердің аумақтық теориясы. Аймақтық теориядағы металдар, өткізгіштер мен Еркін электрондар моделіне сәйкес металл атомдарының валенттілік электрондары үлгінің шегінде еркін орын ауыстыра алады. Металдардың электр өткізгіштігін нақ осы валенттілік электрондар жасайды, осы себебтен оларды өткізгіштік электрондар деп атайды. Еркін электрондарды кристалда бір-біріне жақындатқанда валенттік электрондардың энергиясы квазиүздіксіз өзгереді. Бұл, рұқсат етілген энергия мәндерінің өте көп жақын орналасқан дискретті деңгейлерден тұратынын білдіреді. Шын мәнінде кристалда валенттілік электрондар толығымен еркін қозғала алмайды – оларға тордың периодтық өрісі әсер етеді. Бұл жағдай, валенттік электрондардың энергияларының мүмкін болатын мәндерінің спектрінің бір қатар, рұқсат етілген және тыйым салынған зоналарға ыдырайды (1-сур.). Рұқсат етілген зоналар шегінде энергия квазиүздіксіз өзгереді. Тыйым салынған зоналардағы энергия мәндерін қабылдау мүмкін емес. Фотоөткізгіштік — электрмагниттік сәуле әсерінен заттың электр өткізгіштігінің өзгеруі. Фотоөткізгіштік электрмагниттік сәуленің жұтылуы нәтижесінде жартылай өткізгіштердегі немесе диэлектриктердегі электрондардың энергетик. деңгейлерге тарала орналасуының өзгеруі салдарынан болады. 15. Бір бағыттағы тербелістерді қосу. Векторлық диаграмма. Соғу. Тiзбектегi толық кернеудiң амплитудасын оның бөлiктерiндегi кернеулердiң амплитудалары арқылы өрнектеу үшiн векторлық диаграмма әдiсiн қолданған ыңғайлы. Бұл әдiс тiзбек бөлiктерiндегi кернеулердiң фазаларының әртүрлi екенiн ескеруге мүмкiндiк бередi. Диаграмманы тұрғызу барысында алдымен тiзбектегi токка сәйкес бағытты таңдап алады да соған қатысты кернеулердiң амплитудалық мәндерiн олардың фазалар айырымын ескере отырып салады. Осылай тұрғызылған диаграмма 1 – суретте келтiрiлген. Бұл суреттен тiзбектегi толық кернеудiң амплитудасы (үшбұрыштар үшiн Пифагор теоремасын пайдаланғанда) (1.1) екенi көрiнiп тұр. Онда, айнымалы ток тiзбегi үшiн Ом заңы (1.2) түрiнде жазылады. Бұл өрнектегi (1.3) шамасы тiзбектiң толық кедергiсi болып табылады. 16. Кванттық статистика элементтері.Фазалық кеңістік. Таралу функциялары. Ферми – Дирак және Бозе-Эйнштейн кванттық статистикалары туралы түсінік. Бозондар және фермиондар. кванттық статистика –көп бөлшектерден тұратын кванттық жүйелердің статистикалық физикасы бозе-эйнштейн статистикасы –бозондардан тұратын жүйеге қолданылатын кванттық статистика Ферми-Дирак үлестірілуі –өзара әрекеттестігін есепке алмауға болатын теңбе-тең фермиондардың энергетикалық деңгейлер бойынша үлестірілуін сипаттайтын өрнек. Бұл күйге сәйкес келетін осындай бөлшектердің орта саны Ферми-Дирак үлестірілуімен анықталады: фермион –жартылай бүтін спинге ие болатын бөлшек немесе квазибөлшек. Фермиондарға электрон, протон, нейтрон, кварктар және т.б. жатады Микробөлшектер классикалық статистикадан өзгеше кванттық статистикаға бағынады. Кванттық бөлшектердің статистикасы Ферми–Дирак статистикасы және Бозе–Эйнштейн статистикасы болып екіге ажыратылады. Спиндері жартылай бүтін бөлшектер (электрондар, протондар, нейтрондар, -мезондар, т.б. – “фермиондар”) Ферми–Дирак статистикасының заңдарына бағынады. Кванттық статистиканың басты ерекшелігі – фермиондардың Паули принципіне бағынатындығы. 17. Еркін өшетін тербелістер және оның сипаттамалары. Өшу коффициенті, өшудің логарифмдік декременті. Сапалылық. Өшетін механикалық тербеліс – ортаның кедергісі салдарынан жүйесінің энергиясы кеміп, уақыт бойынша амплитудасы азайып отыратын тербелістер. Кез келген нақты тербеліс жүйесінде тербеліс өшеді. Механикалық тербелістерде өшу ортаның кедергісі, ал электр тізбектерінде өткізгіштің жылу шығару салдарынан болады. Fr=-rv=-rx’ Fcep=-kx мұндағы r – кедергі коэффициенті, «-» таңбасы fr мен v жылдамдық шамаларының бағыттары қарама қарсы . Ньютонның 2 заңынан: F=-Fcep-F, ma= -kx-rV, a=x”, v=x’ , mx’= -kx – rx. 2) mx”+kx+rx’=0 x”+2 x”+w0x=0 – өшетін тербеліс теңдеуі. B - өшу коэффициенті, w0 – жүйенің меншікті жиілігі. Шешімі: x” = a(t)cos(wt+ , a(t) – уақыт бойынша кеміп отыратын амплитудасы, оның мәнін үшін х’ және x” туындыларын 2 теңдеуге қойып, түрлендіреміз. Тербеліс амплитудасы экспоненциал заңымен кемігендіктен, бір периодқа сәйкес уақыт мезетінде амплитудалар қатынасын өшу декрементідеп, оның логарифмі өшудің логарифмдік декременті д.а. A=ln Тербелмелі жүйені сипаттау үшін жүйе сапалылығы деп аталатын физикалық шаманы еңгіземіз: Q = N. 18. Электромагниттік сәуле шығарудың затпен өзара әсерлесуінің кванттық табиғаты. Спонтанды және еріксіз сәуле шығарулар. Лазер. Кванттық көшу – квант жүйесінің секірмелі түрде бір энергетикалық күйден екінші энергетикалық күйге көшуі. Егер атом жоғары энергетикалық күйден төменгіге өтсе сәуле шығарады, керінше болса жұтады. Сәуле шығарудың екі түрі бар: спонтанды және еріксіз. Ал жұтылу тек еріксіз болады. Спонтанды сәуле шығару – сыртқы әсерге байланыссыз, өздігінен сәуле шығары. Шығарылған сәулелер когерентті емес. Атом жоғарғы деңгейден төменгіге түседі. Еркісіз сәуле шығару – сыртқы әсердің ықпалынан сәуле шығару, шығарылған сәулелер толқынының жиілігі, фазасы, поляризациясы атомға түсетін толқынымен дәлме-дәл болады, былайша айтқанда когорентті. Атом жоғарғы деңгейден еріксіз төменгі деңгейге көшеді, интенсивтілігі күшейеді. Лазер дегеніміз – оптикалық сәуле шығаратын кванттық генераторлар көзі. Ол ультра күлгін, көрінетін және инфрақызыл сәулелер аралығын қамтиды. 19. Еріксіз тербелістер. Еріксіз тербеліс фазасы және амплитудасы. Резонанстық қисықтар. Еріксіз тербелістер-Еркін тербелістер әйтеуір бір тоқтайды. Тербелісті өшпейтін ету үшін үйкелісті жеңуге кететін энергияны толықтырып отыру қажет. Тербелмелі жүйенің энергиясын оған сыртқы периодты түрде өзгеріп отыратын күшпен әрекет ету арқылы толықтыруға болады. Жүйенің энергиясы осы сыртқы күш жұмысының есебінен толығады. Бұл жағдайдатербелістер енді еркін емес, еріксіз болады; осы тербелістерді тудырушы периодты түрде өзгеріп отыратын күш мәжбүр етуші күш деп аталады. Сонымен еріксіз тербелістер дегеніміз — сыртқы периодты күштің әрекетіненболатын тербелістер.
|
|
|
|
|
|
|
|
|
|
|
|
Резонанс
Орныққан еріксіз тербелістердің жиілігі қашанда сыртқы күштің жиілігіне тең. Енді осы еріксіз тербелістерамплитудасының жиілікке қалай тәуелді екенін айқындайық.
Керілген жіпке екі маятник ілеміз. Мұндағы А маятнигінің ұзындығы езгермейді. Ал В маятнигінің ұзындығын жіптің бос ұшын әрлі-берлі қозғай отырып өзгертуге болады. Егер маятникті тербеліске келтірсек, онда ол керілген жіп арқылы A маятникке қайсыбір периодты күшпен әрекет етеді. Соның салдарынан енді А маятник те еріксіз тербеле бастайды.
20. Кванттық гармоникалық осциллятор. Нөлдік энергия. Бөлшектердің потенциалды тосқауыл арқылы өтуі.
Кванттык сызыктық гармоникалық оссилятор.
гармоникалық оссилятор квазисерпімді күштің әсерінен бір өлшемді қозғалыс жасайтын жүйе.мұндай жүйе көптеген классикалық есептермен кванттық теорияның моделі ретінде қарастырылады.Кәдімгі серіппелі маятник,физикалық маятниктер г.о ның мысалдары бола алады.
Егер де классикалық механика заңдары бойынша бөлшек потенциялдық шұңқыр координаттары (-xmax+xmax)облысы ішінен шыға алмайды десек кванттық механика теориясы бқлшектің осы облыстан шығып кету ықтималдылығының болуы, толқындық қасиетіне байланысты.
21. Шексіз терең қабырғалы бір өлшемді тік бұрышты потенциалды шұңқырдағы бөлшектер. Бордың сәйкестік принціптері.
Кванттық және классикалық физикалардың айырмашылығын көрсететін тунельдік эффект болып табылады.классикалық механикада егер бөлшектің энергиясы тосқауыл энергиясынан аз болса бөлшек тосқауылдан өте алмайды, ал кванттық физикада өту ықтималдылығы бар. Бұл бөлшектің толқындық қасиетімен түсіндіріледі.
U биіктігі, d ені болатын потенциалдық тосқауылдың сол жағынан келіп түсетін бөлшекті қарастырайық.сурет

Бөлшектің энергиясы тосқауыл потенциялының энергиясынан кем Е<U. Шұңқыр ішіндегі бөлшек үшін Шредингер теңдеуін жазайық

Осы екі дифференциалдық теңдеулердің шешімі
I –аймақ үшін х<0, 
II- аймақ үшін 0<Х<d 
III – аймақ үшін х>dᴪ3(x)= 
Мұндағы К1= 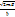 , K2=
, K2= 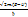
A1  және
және  тосқауылға түсетін ,шағылатын де Бройль толқындары.
тосқауылға түсетін ,шағылатын де Бройль толқындары.  0 шекарасынан сынып өткен толқын, ал
0 шекарасынан сынып өткен толқын, ал 
Х=a шекарасынан шағылған толқын  тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а
тосқауылдан өтіп қайта оралмайтын толқын. Тосқауыл мен бөлшектің айырым энергиясы U~E мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а
22. Толқындық қозғалыстың негізгі сипаттамалары.. Сфералық және жазық толқын. Толқын теңдеуі. Фазалық жылдамдық. Топтық жылдамдық. Толқындық теңдеу.
Толқын тарайтын ортаның бөлшектері толқынмен ілесіп кетпейді, олар өзінің тепе- теідік қалпының маңында ғана тербеледі. Толқын таралатын бағытпен салыстырғандағы бөлшектер тербелістің бағытына байланысты қума және көлденең болып екіге бөлінеді.
Көлденең толқын – ортаның бөлшектері толқынның таралу бағытына перпендикуляр тербеледі.
Қума толқын- ортаның бөлшектері толқынның таралу бағыты бойынша тербеледі.
Механикалықкөлденең толқындар ығысу кедергісі бар ортада ғана пайда бола алады. Сондықтан сұйық және газ тектес ортада тек қума толқын тарай алады. Уақыт өтуіне байланысты орта бөлшектерінің қозғалысы берілген, әр түрлі бөлшектер фазасы бойынша тербеледі.
Толқын ұзындығы- бірдей фазада ең жақын орналасқан бөлшектердің арақашықтығы. 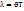 немесе λ=
немесе λ= 
Толқын фронты – бір уақыт мезетінде тербеліс келіп жеткен нүктелердің геометриялық орны.
Толқындық бет – бірдій фазада тербелетін нүктелердің геометриялық орны. Қарапайым толқындық бет жазық немесе сфеоралық болады. Жазық толқында толқындық беттер бір біріне параллель жазықтарда , ал сфералық толқында – концентрлік сфералар түрінде болады.
Толқын теңдеуі тербелістегі нүктенің ығысуын x,y,z координаталары мен t уақыттың функциясы ретінде беретін өрнек.
Фазалық жылдамдық –фазаның орын ауыстыру жылдамдығы. Толқын фазасы 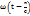 мәнімен анықталады. Берілген фазада барлық нүктедегі тербеліс амплитудасы бірдей болады, олай болса
мәнімен анықталады. Берілген фазада барлық нүктедегі тербеліс амплитудасы бірдей болады, олай болса  . Осы өрнекті диференциалдай отырып фазалық жылдамдығы табамыз. dt- -
. Осы өрнекті диференциалдай отырып фазалық жылдамдығы табамыз. dt- -  =0.
=0. 
 |
Толқындық сан - 2
 ұзындығына қаншалықты толқын ұзындығы сәйкес келетін сан k=
ұзындығына қаншалықты толқын ұзындығы сәйкес келетін сан k= 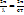 =
=  .
.
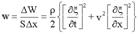 |
Жазық толқын теңдеуін толқындық сан арқылы өрнектейік ξ=acos(
 Негізен л векторлық шама толқынның таралу бағытын көрсетеді k=ki. kx=kr, мұндағы r- радиус векторы, олай болса , кез келген бағытта таралатын жазық толқынның теңдеуі ξ=acos(
Негізен л векторлық шама толқынның таралу бағытын көрсетеді k=ki. kx=kr, мұндағы r- радиус векторы, олай болса , кез келген бағытта таралатын жазық толқынның теңдеуі ξ=acos(  . Изотроптыжәне толқын энергиясын жұтпайтын ортада тарайтын толқын, дербес диференциалдық теңдеуменсипатталады, оны толқындық теңдеу деп атайды. Оның түрі
. Изотроптыжәне толқын энергиясын жұтпайтын ортада тарайтын толқын, дербес диференциалдық теңдеуменсипатталады, оны толқындық теңдеу деп атайды. Оның түрі 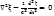 мұндағы
мұндағы  Лаплас операторы. Жазық толқынның осы теңдеуі қанағаттандыратын дәлелдеік.
Лаплас операторы. Жазық толқынның осы теңдеуі қанағаттандыратын дәлелдеік.  acos(
acos( 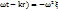 , (7)
, (7)
 acos(
acos( 
 acos(
acos( 
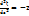 acos(
acos(  ,
,
 |
 ., ξ=-
., ξ=-  олай болса
олай болса  ,
,  ,
, 
 |

Лаплас операторы арқылы жазсақ 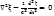 дәлелдеу керегі де осы еді. Толқынның энергиясы.
дәлелдеу керегі де осы еді. Толқынның энергиясы.
Серпімді ортада тарайтын толқын энергиясы тербеліс жасайтын бөлшектердің кинетикалық энергиясы мен деформация салдарынан туатын потенциялдық энергияның қосындыларынан тұрады. Жазық қума толқын таралатын  элементар көлем бөліп алайық Ек және Ер энергиялары
элементар көлем бөліп алайық Ек және Ер энергиялары  мұндағы
мұндағы  ,
,  жылдамдығы.
жылдамдығы.
Толқын энергиясы 
Энергияның тығыздығы w= 
Жазық толқын үшін 
Онда w=  орташа мәні
орташа мәні  . Тараған толқынн көзімен бірге энергия тығыздығы да тасымалданады. Кеңістіктің әр түрлі нүктелеріндегі энергия ағынын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама еңгізу, оны алғашқы рет Н. Умов енгізгін j=
. Тараған толқынн көзімен бірге энергия тығыздығы да тасымалданады. Кеңістіктің әр түрлі нүктелеріндегі энергия ағынын сипаттау үшін энергия ағынының тығыздығы деп аталатын векторлық шама еңгізу, оны алғашқы рет Н. Умов енгізгін j= 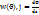 . Мұндағы Ф энергия ағыны Ф=
. Мұндағы Ф энергия ағыны Ф= 
Умов векторының абсолюттік шамасы толқынның интенсивтілігін береді. I=│  │, I=│
│, I=│  │=
│=  . Амплитудасы A=
. Амплитудасы A= 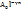 интенсивтілігі I=
интенсивтілігі I=  . Жұтылатын ортадағы жазық толқынның теңдеуі
. Жұтылатын ортадағы жазық толқынның теңдеуі 
23. Шредингердің уақыттық және стационар теңдеуі. Қарапайым кванттық жүйе үшін Шредингер теңдеуінің шешімі. Бордың сәйкестік принципі.
1.Шредингер теңдеуі. Шредингердің стационар теңдеуі
Кванттық механиканың негізігі теңдеуі болып, толқындық функцияға арналған Шредингердің 1926ж ашқан ұсақ бөлшектер күйін сипаттатйтын теңдеуі жатады. Бұл теңдеу бұрыннан белгілі қатынастардан қорытылып шығарылмай, тек көптеген ғылыми тәжірибелердің нәтижелерінен табылады. Шредингер теңдеуінің жалпы түрі: -  (1)
(1)
Мұндағы h=h/2п=1,05*10-34 Дж*с, m-бөлшектің массасы, U=(x,y,z,t)-күштер өрісіндегі бөлшекте потенциалдық энергиясы, i- жорамал сан, 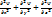 - бөлшектің кеңістіктегі координаты.
- бөлшектің кеңістіктегі координаты.
(1) теңдеудегі Ψ функциясы потенциалдық өрістегі бөлшекке әсер ететін күштердің потенциалдық энергиясы арқылы анықталады. Сөйтіп, U потенциалдық энергия уақыт пен кордината фунциясы екендігін байқаймыз, яғни Ψ(х,у,z,t)  Е – бөлшектің толық энергиясы. Егер (2) өрнекке 1 теңдеудегі функция мәндерін қойып, дифференциалдық теңдеуін аламыз:
Е – бөлшектің толық энергиясы. Егер (2) өрнекке 1 теңдеудегі функция мәндерін қойып, дифференциалдық теңдеуін аламыз:  (3) Осы теңдеу Шредингердің бөлшектің стационарлық күйін сипаттайтын теңдеу.
(3) Осы теңдеу Шредингердің бөлшектің стационарлық күйін сипаттайтын теңдеу.
2.Потенциал U(r)=e2z/r тең ядроның центрлік өрісіндегі қозғалатын электронды қарастырайық. Егер z>1 болса сутек тәріздес атом дар, ал z=1 сутегі атомын аламыз. Өріс центрін – симетриялы болғандықтан сфералық кординатта жүйесін қолдануға тиімді. Сфералық координатасындағы Шредингер теңдеуі
 (r2
(r2  )+
)+ 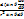 +
+ 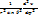 =
= 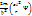 =Eᴪ
=Eᴪ
Теңдеудің шешімі болу үшін ᴪ функциясы бір орында бір мәнді шектеулі үздіксіз болу керек. Энергияның мәні Еn= - 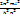 .Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
.Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
24. Серпінді толқын энергиясы. Энергия ағынының тығыздығы. Умов векторы
22-сұрақ қара.
.,
тығыздылық:.
Энергия:
25. Толқындардың суперпозиция принціпі. Топтық жылдамдық пен фазалық жылдамдық және олардың арасындағы байланыс. Толқындардың интерференциясы.
Толқындардың суперпозиция принципі- егер ортада бір мезгілде бірнеше толқын тараса онда орта бөлшектерінің тербелісі, әрбір толқын жеке-жеке тараған кезде бөлшектер жасайтын тербелістің векторлық қосындысына тең. 
Бұдан толқындар бірін бірі ұйытқытпай, бір бірімен қабаттасады. Кез келген күрделі толқында жиіліктері әр түрлі синусоидалық толқындардың қосындысынан тұрады, екінші сөзбен айтқанда топтық толқыннан немесе толқындық пакет ретінде қарастыруға болады. Бұл толқындар жиіліктерінің жиынтығы спектр деп аталады. Спектр дискрентті немесе тұтас болады. Күрделі синусоидалық толқындарға жіктеуін Фурье қатарына жіктелуі деп аталады.
Топтық жылдамдық- кез келген бір берілген толқын амплитудасының таралу жылдамдығы. Топтық жылдамдық толқын тасымалдайтын энергиясының жылдамдығына тең. Дисперсия болмайтын ортада синусоидалдық толқындардың фазалық жылдамдықтары жиіліктеріне байланысты емес, сондықтан фазалық жылдамдықтары бірдей. Олай болса күрделі толқынның таралу кезінде пішіні өзгермейді. Дисперсия құбылыс байқалатын ортада фазалық жылдамдықтары жиілікке тәуелді болғандықтан, жиіліктері әр түрлі синусоидалдық толқындар әр түрлі жылдамдықпен тарайды. Осы толқындардан тұратын күрделі толқын ортада тұрғанда «жәйіліп» өз пішінін өзгертеді. Екі синусоидалдық толқындардан тұратын толқынның топтық жылдамдығын қарастырайық. Амплитудалары бірдей, жиіліктері мен толқындық сандары бір-біріне жақын толқындар болсын.
ԑ= 
Толқынның топтық жылдамдығы U кез келген берілген толқын амплитудасын таралу жылдамдығын алуға болады. М нүктесінің қозғалыс заңы  олай болса
олай болса  топтық жылдамдықтың формуласы. Топтық жылдамдық пен фазалық жылдамдықтың арасындағы байланыс.
топтық жылдамдықтың формуласы. Топтық жылдамдық пен фазалық жылдамдықтың арасындағы байланыс.
 ,
,  өрнегін дифференциялдайық
өрнегін дифференциялдайық 
Егер  болса қалыпты дисперсия (U˂V), ал
болса қалыпты дисперсия (U˂V), ал  дисперсия деп аталады,
дисперсия деп аталады,  =0 дисперсия болмайтын орта (U=V).
=0 дисперсия болмайтын орта (U=V).
Жарық интерференциясы дегеніміз екі немесе одан да көп когорентті толқындардың бірін бірі күшейту және әлсірету құбылысы. Бақылау үшін Ньютон сақинасын қолданады. Минималдық шарт:  Фазалық жылдамдық – тұрақты фазасы бар нүктенің қозғалыс жылдамдық немесе фазалардың өзгеру жылдамдығы.
Фазалық жылдамдық – тұрақты фазасы бар нүктенің қозғалыс жылдамдық немесе фазалардың өзгеру жылдамдығы.  ,
,  . Топтық жылдамдылық
. Топтық жылдамдылық  . Суперпозиция принципі:
. Суперпозиция принципі: 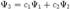 .
.
26.Сутегі атомы үшін Шредингер теңдеуі. Энергетикалық деңгейлер. Деңгей ені. Спин.Кеңістіктің квантталуы. Паули принципі.
Потенциал U(r)=e2z/r тең ядроның центрлік өрісіндегі қозғалатын электронды қарастырайық. Егер z>1 болса сутек тәріздес атом дар, ал z=1 сутегі атомын аламыз. Өріс центрін – симетриялы болғандықтан сфералық кординатта жүйесін қолдануға тиімді. Сфералық координатасындағы Шредингер теңдеуі
 (r2
(r2  )+
)+ 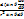 +
+ 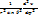 =
= 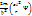 =Eᴪ
=Eᴪ
Теңдеудің шешімі болу үшін ᴪ функциясы бір орында бір мәнді шектеулі үздіксіз болу керек. Энергияның мәні Еn= - 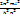 .Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
.Яғни Бор теориясымен сәйкес болады n бас квант саны,мәні n=1,2…
Берілген n үшін l ие мәндерге ие болады l=0,1…n-1. l саны азимуталдық кванттық сан д.а.l cаны электронның орбита бойымен айналу пішіндерінің түрлерін көрсетеді.l=0 болса сопақ эллипс . l=n-1 дөңгелеккеlжақын эллипс. Орбиталды момент импульсінің шамасы кез келген l шамасы Le =ђ 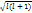
Үшінші кванттық сан магниттік кванттық сан деп m әріпімен белгілейміз. Ол берілген l үшін – l мен l аралығында жатады. Мәні L=mђ
Cонымен n- энергияны сипаттайтын бас кванттық сан, l -импульс моментін сипаттайтын азимуталдық кванттық сан, m-импульс моментінің сыртқы өріске проекциясын сипаттайтын магниттік кванттық сан.
Электронның спині. Магнит өрісінде атомдар деңгейінің жіктелуін бірінші рет Штерн мен Герлах зертеген.Тәжірибеде атомдар шоғы бір текті емес магнит өрісінен өткізілген.Бұндай магнит F=ϻdB/dz күш әсер етеді. Егер сутегі атомы S күйінде болғанда (l=0) магнит моменті 0-ге тең. Орбиталды моменті сияқты спиндік кванттық санын S деп және 2S+1 энергетикалық күйінде бола алады.Электронның меншікті импульс моментінің шамасы
M=ђ 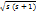 =ђ
=ђ 
немесе одан да көп электрондар бір мезгілде бір күйде бола алмайды.Паули принципі элементтердің электрондық конфигурациясын құрғанда
сутегі атомындағы электронның потенциалдық функциясы: 
 .,
.,  . Энергетикалық деңгей — кванттық механика заңдарына бағынатын, белгілі бір кванттық жүйе энергиясына тең дейгей. ∆ε ∆t≥h энергетикалық деңгей енінің Гейзенберг анықталмағандығы арқылы жазу. Спин — элементар бөлшектің меншікті өзгермейтін импульс моменті және бөлшектің тұтастық ретінде қозғалысына байланысы жоқ, оның кванттық табиғатын сипаттайтын мағына. Паули принципі – атом ішінде бір уақытта төрт квант саны бірдей электрон бола алмайды
. Энергетикалық деңгей — кванттық механика заңдарына бағынатын, белгілі бір кванттық жүйе энергиясына тең дейгей. ∆ε ∆t≥h энергетикалық деңгей енінің Гейзенберг анықталмағандығы арқылы жазу. Спин — элементар бөлшектің меншікті өзгермейтін импульс моменті және бөлшектің тұтастық ретінде қозғалысына байланысы жоқ, оның кванттық табиғатын сипаттайтын мағына. Паули принципі – атом ішінде бір уақытта төрт квант саны бірдей электрон бола алмайды
27. Кванттық механикадағы микробөлшектердің күйі. Толқындық функция және оның статистикалық мағынасы. Шредингердің уақыттық және стационар теңдеуі
«Шредингердің уақыттық және стационар теңдеуі» жоғарыда болды.
Толқындық фу́нкция дегеніміз (пси-функция) — кванттық физикадағы жүйенің квантомеханикалық күйін сипаттайтын комплексті функция.  , Нормалау шарты:
, Нормалау шарты:  , Шредингер теңдеуі:
, Шредингер теңдеуі: 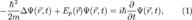 ,
, 
 .
.
28. Электромагниттік өріс үшін толқын теңдеу. Толқындық теңдеу. Электромагнитті толқын қасиеттері.
Толқындық теңдеу деп – х, у, я координаталары бойынша нүктенің тербелу заңдылығы немесе толқынның таралу заңдылығы деп түсінуге болады: 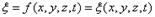 . Жазық толқынның теңдеуі:
. Жазық толқынның теңдеуі:  . Толқындық сан:
. Толқындық сан:  .
.
Максвеллдан алынды. Примерно келеді деп ойлайм
Электромагнит өрісінің теориясын К.Максвелл зерттеп жетілдірді. Бұл теория бойынша:
1)электромагнит өріс екі құраушыдан тұрады:электр және магнит өрістері, олар бір-бірін туғызып ажырамастай байланыста болады.
2)электромагнит өрісі вакуумде жарық жылдамдығымен тарайды;
Максвеллдің төрт теңдеулері ортаның қасиеттерін сипаттайтын материялық теңдеулермен толықтырылады D= 
Ығысу тогы. Фарадейдің электромагнит индукция заңынан айнымалы магнит өріс айнымалы электр өрісін туғызады.Максвелл осы сияқты айнымалы электр өрісі магнит өрісін туғызу керек деген болжам жасаған, кейіннен бұл тәжірбие жүзінде дәлелденген. Бір конденсатор алайық, тұрақты көзіне қосайық. Тұрақты ток өту үшін тізбек тұйықталған болу керек, конденсатор арасы диэлектрикпен толтырылғандықтан, тізбекте ток тумайды. Егер корденсаторды айнымалы ток көзіне қоссақ ток пайда болады. Максвеллдің теориясы бойынша кез-кеген айнымалы ток үшін тізбек тұйықталған болып есептеледі және ығысу тогы деген физикалық шамамен сипатталады. Ыгысу тогы айнымалы магнит өрісін туғызады. Сонымен берілген тәжірбиеден айнымалы электр өрісі айнымалы магнит өрісін туғызатынын көреміз. Ығысу тогының шамасын неге байланысты екенін анықтайық. Остроградский-Гаусс теоремасынан электр өрісінің ағыны  бұдан уақыт бойынша туында алсақ
бұдан уақыт бойынша туында алсақ  және беттік ауданы өзгермесе дербес туынды арқылы жазамыз
және беттік ауданы өзгермесе дербес туынды арқылы жазамыз  екенін ескерсек j=
екенін ескерсек j=  –ығысу тогының тығыздығын аламыз. Бұдан уақыт бойынша өзгеретін электр ығысуы кеңістік те ток ығысуын туғызады, екінші жағынан айнымалы ток ығысуы айнымалы магнит өрісін туғызады, Өткізгіш үшін толык ток тығыздығы jтолык=jот+jығы= jот+
–ығысу тогының тығыздығын аламыз. Бұдан уақыт бойынша өзгеретін электр ығысуы кеңістік те ток ығысуын туғызады, екінші жағынан айнымалы ток ығысуы айнымалы магнит өрісін туғызады, Өткізгіш үшін толык ток тығыздығы jтолык=jот+jығы= jот+  .
.
Интеграл түріндегі Максвеллдің төрт теңдеуі
 физикалық мағынасы:уақыт бойынша өзгеретін магнит индукциясы кеңістікте құйынды электр өрісін туғызады.
физикалық мағынасы:уақыт бойынша өзгеретін магнит индукциясы кеңістікте құйынды электр өрісін туғызады.
 немесе
немесе  Физикалық мағынасы:магнит өрісі өткізгіштік ток пен ығысу тогынан пайда болады немесе уақыт бойынша өзгеретін электр индукциясы құйынды магнит өрісін туғызады.
Физикалық мағынасы:магнит өрісі өткізгіштік ток пен ығысу тогынан пайда болады немесе уақыт бойынша өзгеретін электр индукциясы құйынды магнит өрісін туғызады.
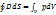 физикалық мағынасы:заряд электр ығысуының көзі болып табылады, электростатистикалық өрісте электр ығысуы зарядтан басталып, содан аяқталады.
физикалық мағынасы:заряд электр ығысуының көзі болып табылады, электростатистикалық өрісте электр ығысуы зарядтан басталып, содан аяқталады.
 Физикалық мағынасы: магнит индукциясының электр ығысуы сияқты зарядтың көздері болмайды. Магнит индукциясын туғызатын ток зарядтардың қозғалысынан пайда болады.
Физикалық мағынасы: магнит индукциясының электр ығысуы сияқты зарядтың көздері болмайды. Магнит индукциясын туғызатын ток зарядтардың қозғалысынан пайда болады.

1)Сток теоремасынан  екінші жағынан
екінші жағынан  олай болса rotE=-
олай болса rotE=-  .
.
2) Сток теоремасынан  екінші жағынан
екінші жағынан  олай болса rotH=
олай болса rotH=  .
.
3) 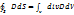 екінші жағынан
екінші жағынан  олай болса
олай болса 
4) Гаусс теоремасынан  бұдан divB=0.
бұдан divB=0.
Сонымен rotE=-  және divB=0 теңдеулерін Максвелл теңдеулерінің бірінші қосағы, ал rotH=
және divB=0 теңдеулерін Максвелл теңдеулерінің бірінші қосағы, ал rotH=  және
және  теңдеулерін екінші қосағы деп атайды.
теңдеулерін екінші қосағы деп атайды.
29. Жарық толқыны және оның сипаттамалары. Жарықтың монохраматтылығы және когеренттілігі. Жарық жылдамдығын анықтау тәжерибелері.
Тербелістің таралу процессі толқын деп аталады. Егер екі немесе одан да көп толқынның жиіліктері бірдей, ал амплитудасы мен фазалар айырымы уақыт бойынша өзгермесе, онда олар когорентті деп аталады. Монохромат – жиіліктері бірдей немесе бір-біріне өте жақын толқындар.
Когерентті толқындар- жиіліктері бірдей және фазалар айырымы уақыт бойынша өзгермейтін толқындар.
Интерференция- жарық толқындарының кеңістікте қабаттасу нәтижесінде бірін бірі күшейтуі немесе әлсіретуі. Интерференция болу үшін толқындар когерентті болуға тиіс. Егер толқындар когерентті болмаса, онда толқындар интенсивтілігінің қосындыларын аламыз, интерференция құбылысы байқалмайды. Жарық толқыны көлденең болғандықтан инт.болуы үшін электр өрісінің векторларының бағыттары бірдей түзудің бойымен тербелуі тиіс. Лазерлер толқынынан басқа жарық көздерінен когерентті толқындар алу үшін, бір қосақ жарық толқынын екіге айыру нәтижесінде аламыз. Суретте көрсетілгендей параллель түскен бір толқыннан S1 және S2 тесіктерден өтетін когерентті толқындар аламыз. Экран бетінде ашық және күңгірт жолақтар, яғни инт.көрінісі байқалады. Толқындар фазалары бірдей болса, толқындар бір бірін күшейтеді. Қарама қарсы болса әлсіретеді. Күшейту немесе әлсірету жол айырмасына байланысты. Кеңістіктегі кез келген нүктедегі қорытқы амплитудасы  бұдан егер фазалар айырмасы
бұдан егер фазалар айырмасы  болса, онда cos
болса, онда cos  болады да
болады да 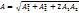 тербеліс амплитудасы максимум мәнге ие болып, бір бірін күшейтеді. Сонымен жолдаар айырмасы жарты толқындардың жұп санына тең болса, онда жарық толқындары бірін бірі күшейтеді.
тербеліс амплитудасы максимум мәнге ие болып, бір бірін күшейтеді. Сонымен жолдаар айырмасы жарты толқындардың жұп санына тең болса, онда жарық толқындары бірін бірі күшейтеді. 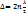 Осы тәріздес
Осы тәріздес  жолдар айырмасы жарты толқындардың тақ санына тең болса, онда жарық толқындары бірін бірі әлсіретеді. Көршілес екі жарық жолақтың ара қашықтығы
жолдар айырмасы жарты толқындардың тақ санына тең болса, онда жарық толқындары бірін бірі әлсіретеді. Көршілес екі жарық жолақтың ара қашықтығы 
30. Заттардың корпускулалық-толқындық дуализмді. Де Бройль гипотезасы және оны тәжерибелермен растау. Де Бройль толқынының қасиеттері.
Де –Бройл болжамы – кез келген бөлшекті толқын ретінде қарастыруға болады . толқын ұзындығы бөлшектін импульсына байланысты және де Де –Бройл ұзындығы деп аталады. λ=h/P=h/mv.
Массасы m бөлшектің v жылдамдықпен еркін қозғалуын қарастырамыз. Ол үшін Де –Бройл толқындаарының фазалық және топтық жылдамдықтарымен есептеп шығарамыз
Vфаза = ω/к=ђω/ђk=E/P=mc2 /mv=c2 /v
(k=2π/λ -толқын саны) өйткені с>v онда де-Бройл толқындарының фазалық жылдамдығы vфаза>с.
Еркін бөлшектер үшін E= 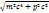
dE/dp=pc2/ 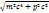 =pc2/E=mvc2/mc2=v осылайша Де-Бройл толқындарының топтық жылдамдығы бөлшектердің жылдамдықтарына тең. Фотонның топтық жылдамдығы u=pc2/E=mcc2/mc2=c яғни фотонның өзінің жылдамдықтарына тән. Деөбройл толқықндары дисперсияға ұшырайды. Шынында Е=
=pc2/E=mvc2/mc2=v осылайша Де-Бройл толқындарының топтық жылдамдығы бөлшектердің жылдамдықтарына тең. Фотонның топтық жылдамдығы u=pc2/E=mcc2/mc2=c яғни фотонның өзінің жылдамдықтарына тән. Деөбройл толқықндары дисперсияға ұшырайды. Шынында Е= 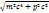 формуласын vфаза=E/p формулаға қойып Де-Бройл толқындарының жылдамдығы толқындар ұзындығына тәуелді. Бұл мән жағдай өз уақытында кванттық механика ережелерін дамытуда үлкен рөл атқарады. Корпускулалық толқындық дуализм орнағаннан кейн бөлшектердің корпускулалық қасиеттерін толқындық қасиеттермен байланыстыруға және бөлшектерді де-Бройл толқындарын ан жасалған(тар) толқындық түйдектер ретінде қарастыруға талпыныс жасалды. Бұл бөлшектердің екі жақтылық қасиеттерінен арылуға мүмкіндік береді. Осындай гипотеза уақыттың аталған мезетінде бөлшектерді кеңістіктің белгілі бір шектелген аймағында локализациялауға сәйкес келді.
формуласын vфаза=E/p формулаға қойып Де-Бройл толқындарының жылдамдығы толқындар ұзындығына тәуелді. Бұл мән жағдай өз уақытында кванттық механика ережелерін дамытуда үлкен рөл атқарады. Корпускулалық толқындық дуализм орнағаннан кейн бөлшектердің корпускулалық қасиеттерін толқындық қасиеттермен байланыстыруға және бөлшектерді де-Бройл толқындарын ан жасалған(тар) толқындық түйдектер ретінде қарастыруға талпыныс жасалды. Бұл бөлшектердің екі жақтылық қасиеттерінен арылуға мүмкіндік береді. Осындай гипотеза уақыттың аталған мезетінде бөлшектерді кеңістіктің белгілі бір шектелген аймағында локализациялауға сәйкес келді.
ᴪ(x,y,z,t) ықтималдық амплитудасы деп аталатын шама ұсынды. Бұл шаманы, сондай ақ толқындық функция деп атайды. Ықтималдық амплитудасы кешенді және W ықтималдылық оның модулінің квадратына пропорционал болуы мүмкін. W ̴ |ᴪ(x,y,z,t)|2 Осылайша толқындық функциялардың көмегімен микрообьектінін күйін сипаттау статистикалық ықтималдық сипатқа ие. Толқындық модулінің квадраты х және х+dx, y+dy, z+dz кординаттарымен аймақты t уақыт мезетінде бөлшектеріндің болу ықтималдығы анықтайды. W=  . Ықтималдықты нормалау шарты
. Ықтималдықты нормалау шарты  .
.
26.Сутегі атомы үшін Шредингер теңдеуі. Энергетикалық деңгейлер. Деңгей ені. Спин.Кеңістіктің квантталуы. Паули принципі.
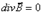


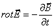 Энергетикалық деңгей — кванттық механика заңдарына бағынатын, белгілі бір кванттық жүйе энергиясына тең дейгей. ∆ε ∆t≥h энергетикалық деңгей енінің Гейзенберг анықталмағандығы арқылы жазу. Спин — элементар бөлшектің меншікті өзгермейтін импульс моменті және бөлшектің тұтастық ретінде қозғалысына байланысы жоқ, оның кванттық табиғатын сипаттайтын мағына. Паули принципі – атом ішінде бір уақытта төрт квант саны бірдей электрон бола алмайды
Энергетикалық деңгей — кванттық механика заңдарына бағынатын, белгілі бір кванттық жүйе энергиясына тең дейгей. ∆ε ∆t≥h энергетикалық деңгей енінің Гейзенберг анықталмағандығы арқылы жазу. Спин — элементар бөлшектің меншікті өзгермейтін импульс моменті және бөлшектің тұтастық ретінде қозғалысына байланысы жоқ, оның кванттық табиғатын сипаттайтын мағына. Паули принципі – атом ішінде бір уақытта төрт квант саны бірдей электрон бола алмайды
КОЛМЕН ЖАЗАМИЗ
27. Кванттық механикадағы микробөлшектердің күйі. Толқындық функция және оның статистикалық мағынасы. Шредингердің уақыттық және стационар теңдеуі
Кванттық механикада микробөлшектердің күйі кеңістіктік координаттар және уақыт функциясы болып табылатын  толқындық функциямен беріледі. Релятивистік емес жағдайда бұл күйдің уақыт бойынша өзгеруі, яғни микробөлшектердің динмикасы кванттық теориялардың негізгі теңдеуі - Шредингер теңдеуімен сипатталады.
толқындық функциямен беріледі. Релятивистік емес жағдайда бұл күйдің уақыт бойынша өзгеруі, яғни микробөлшектердің динмикасы кванттық теориялардың негізгі теңдеуі - Шредингер теңдеуімен сипатталады.
 комплексті функциясының
комплексті функциясының  модулының квадраты координаттары x,y,z болатын нүкте айналасындағы
модулының квадраты координаттары x,y,z болатын нүкте айналасындағы  көлемде бөлшектердің болу ықтималдығының тығыздығын береді. Микробөлшектерді t уақыт мезетінде осы көлем ішінде болу ықтималдығы келесі өрнекпен беріледі
көлемде бөлшектердің болу ықтималдығының тығыздығын береді. Микробөлшектерді t уақыт мезетінде осы көлем ішінде болу ықтималдығы келесі өрнекпен беріледі
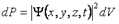 . (11.1)
. (11.1)
 функциясы өзінің мағынасы бойынша қандай да бір шарттарды қанағаттандыруы қажет. Толқындық функция барлық жерде үздіксіз және бірмәнді болуы керек. Сонымен қатар (11.1) өрнегімен анықталатын ықтималдық толқындық функцияның нормалдау шартына сәйкес бірге тең болуы тиіс.
функциясы өзінің мағынасы бойынша қандай да бір шарттарды қанағаттандыруы қажет. Толқындық функция барлық жерде үздіксіз және бірмәнді болуы керек. Сонымен қатар (11.1) өрнегімен анықталатын ықтималдық толқындық функцияның нормалдау шартына сәйкес бірге тең болуы тиіс.
 .
.
Шредингердің уақыттық теңдеуі: 
мұндағы  - жорамал бірлік;
- жорамал бірлік;  - бөлшек массасы;
- бөлшек массасы;  - Лаплас операторы;
- Лаплас операторы;  - микробөлшектің потенциалдық энергиясы.
- микробөлшектің потенциалдық энергиясы.
Кванттық механикада микробөлшек стационар күш өрісінде орналасқан және оның потенциалдық энергиясы уақытқа тәуелді емес болатын, стационар есептер көптеп кездеседі. Шредингердің стационар теңдеуі  Бұл теңдеудегі
Бұл теңдеудегі  параметрінің
параметрінің
мағынасы бөлшектің толық энергиясы, ал бұл теңдеудің  шешімі кеңістіктік координатар функциясы болып табылады. Шредингер теңдеуі дербес туындылы теңдеу және оның шешімі үшін бастапқы және шекаралық шарттар берілуі қажет.
шешімі кеңістіктік координатар функциясы болып табылады. Шредингер теңдеуі дербес туындылы теңдеу және оның шешімі үшін бастапқы және шекаралық шарттар берілуі қажет.
Берілген  жағдайда теңдеуін қанағаттандыратын
жағдайда теңдеуін қанағаттандыратын  функциясы меншікті функция, ал теңдеудің шешімінен шығатын
функциясы меншікті функция, ал теңдеудің шешімінен шығатын  энергия мәндері меншікті мәндер деп аталады.
энергия мәндері меншікті мәндер деп аталады.
28. Электромагниттік өріс үшін толқын теңдеу. Толқындық теңдеу. Электромагнитті толқын қасиеттері.
электрмагниттік өріс уақыт пен кеңістік бойынша таралады. Бұл процесс периодты және электрмагниттік толқындеп аталады.
 Максвелл теориясына сәйкес, еркін электр зарядтарынан да (p=0) және макроскопиялық (j=0) токтардан да қашықта орналасқан электромагниттік толқындар үшін (1.1-кестедегі 1-4) теңдеулер мына түрде жазылады.
Максвелл теориясына сәйкес, еркін электр зарядтарынан да (p=0) және макроскопиялық (j=0) токтардан да қашықта орналасқан электромагниттік толқындар үшін (1.1-кестедегі 1-4) теңдеулер мына түрде жазылады.
 ,
,
байланысын ескеріп, жазатын болсақ:




 мұндағы m (miu) және e (epselon) - ортаның тұрақты өтімділіктері.
мұндағы m (miu) және e (epselon) - ортаның тұрақты өтімділіктері.
(6.2) электрмагниттік толқынның толқындық теңдеулері болып табылады. Бұл теңдеулердің шешімдері
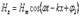
 теңдеулерден электрмагниттік толқынның негізгі қасиеттері шығады.
теңдеулерден электрмагниттік толқынның негізгі қасиеттері шығады.
КОЛМЕН МЕТОДИч КАДАН ЖАЗ 24БЕТ
29. Жарық толқыны және оның сипаттамалары. Жарықтың монохраматтылығы және когеренттілігі. Жарық жылдамдығын анықтау тәжерибелері.
Жарық — электромагниттік толқын.Айнымалы электромагниттік өріс тербелістерінің кеңістікте таралуын электромагниттік толқын деп атайды. Электрмагниттік өрістің әрбір нүктесінде E жәнеH векторлары бірдей жиілікпен гармоникалық тербеледі. Сондықтан электрмагниттік толқын монохроматтыболып табылады.Когерентті толқынның жиіліктері бірдей фазалар айырымы тұрақты болады.Электромагниттік толқынның таралу жылдамдығы:
 м\с, (3.1)
м\с, (3.1)
мұндағы 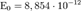 Ф\м — электрлік және
Ф\м — электрлік және  Гн\м— магниттік тұрақтылар. Бұл электромагниттік өрістің іргелі қасиеті. Электромагниттік толқынның ортадағы таралу жылдамдығы Максвелл формуласы бойынша анықталады:
Гн\м— магниттік тұрақтылар. Бұл электромагниттік өрістің іргелі қасиеті. Электромагниттік толқынның ортадағы таралу жылдамдығы Максвелл формуласы бойынша анықталады:
 , (3.2)
, (3.2)
мұндағы  — ортаның сыну көрсеткіші,
— ортаның сыну көрсеткіші,  — ортаның диэлектрлік және
— ортаның диэлектрлік және 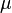 — магниттік өтімділіктері. ДАПТЕР ФОРМУЛА КЫСКАША
— магниттік өтімділіктері. ДАПТЕР ФОРМУЛА КЫСКАША
30. Заттардың корпускулалық-толқындық дуализмді. (1924)Де Бройль гипотезасы және оны тәжерибелермен растау. Де Бройль толқынының қасиеттері.
Фотоэффекті,Комптон эффектісі, жарықтың қысымын қарастырғанда, жарықтың фотондар ағыны ретінде қарастардық. Сонымен қатар дифракция мен интерференция құбылыстары жарықтың толқындық қасиеттері бар екендігін дәлелдейді. Олай болса жарықтың екі жақтылығын көреміз, оны корпускулалық-толқындық дуализмі деп атайды. Дене бетіне жарық келіп түссін. Толқындық тұрғыдан дененің жарықталуын жарық толқынының интенсивтілігіне тура пропорционал, ал корпускулалық тұрғыдан фотондар ағынының тығыздығына тура пропоционал. Олай болса жарық интенсивтілігі фотондар ағынының тығыздығымен анықталады. Бұдан жарықтың толқындық және корпускулалық қасиеттерін бірін-бір жоймай, керісінше толықтырады. Классикалық физикада бөлшек пен толқынның табиғатын әртүрлі деп қарастырады. Бөлшек дискретті, кеңістікте өте аз көлем алады, ал толқын болса кеңістікте өте үлкен орын алады.
Де Бройль теориясы бойынша кез келген микрообъектінің бір жағынан корпускулалық сипаттамалары болады: энергия  , импульс
, импульс  , екінші жағынан толқындық сипаттамалары болады: жиілік
, екінші жағынан толқындық сипаттамалары болады: жиілік  , толқын ұзындығы
, толқын ұзындығы  . Кез келген бөлшектің корпускулалық-толқындық сипаттамалары дәл фотонның сипаттамалары сияқты байланысқан: ħ=h/2πкелтірілген планк турактысы
. Кез келген бөлшектің корпускулалық-толқындық сипаттамалары дәл фотонның сипаттамалары сияқты байланысқан: ħ=h/2πкелтірілген планк турактысы
 ,
,  .
.
Де Бройль гипотезасын америка ғалымдары К.Девиссон мен Л.Джемер эксперимент жүзінде электрондар ағынының интерференциясын зерттегенде дәлелдеді. П.С. Тартаковский және Г.П. Томсон бір-біріне тәуелсіз электрондардың металл фольгадан өткен кездегі дифракциясын бақылады. Л.М. Биберман, Н.Г. Сушкин и В.А. Фабрикант (1949 ж.) тәжірибелерінде толқындық қасиеттер микробөлшектер ағынына емес, жекелеген микробөлшектерге тән екенін дәлелденді.
Де Бройль толқынының қасиеттері.
ДАПТЕР ФОРМУЛА КЫСКАША
31. Жарық интерференциясы және оны бақылау тәсілдері.
Фазалар ығысуы тұрақты және жиіліктері бірдей толкындардың қосылуы жарық толқындарының өзара әрекеттесуі кезінде кеңістіктің кейбір нүктелерінде толқындардың қабаттасуынан бір-бірін күшейтетін, ал басқа бір нүктелерінде керісінше бір-бірін әлсірететін интерференция құбылысы байқалады. Экранда күңгірт және ашық жолақтар кезектесіп орналасады. Бұл интерференция құбылысы болу шарттары:Қосылатын жарықтар когерентті болу керек, яғни жиіліктері бірдей,фазалар айырымы тұрақты.Интерференция құбылысын бақылауды 3 әдісі бар.Олар: Юнг әдісі, Френел әдістері. Жұқа пленка әдісі.МАХ МІN шарттары
ДАПТЕР ФОРМУЛА КЫСКАША
32. Комптон эффектісі және оның элементар теориясы.
Комптон эффектісі – рентген сәулесі шашыраған кезде олардың толқын ұзындығының өзгеруі жарықтың корпускалық қасипетінің айқын дәлелі комптон эффектісі болып табылады. Толқын ұзындықтарының айырмасы  шашыратқыш затқа ж/е түскен сәуленің толқынының ұзындығына тәуелді болмай, тек шашыраған сәулелердің шашырау боғытына байланысты
шашыратқыш затқа ж/е түскен сәуленің толқынының ұзындығына тәуелді болмай, тек шашыраған сәулелердің шашырау боғытына байланысты  . Мұндағы
. Мұндағы  м – комптон толқын ұзындығы,
м – комптон толқын ұзындығы,  шашыраған сәуленің толқын ұзындығы
шашыраған сәуленің толқын ұзындығы  -шашырау бұрышы.
-шашырау бұрышы.
ДАПТЕР ФОРМУЛА КЫСКАША
33. Жарыққ дифракциясы. Гюгенс-Френель принціпі. Френельдің зоналар әдісі.
Жарық дифракциясы — жарық толқындарының мөлшері сол толқындардың ұзындығымен қарайлас тосқауылды (тар саңылау, жіңішке сым, т.б.) орап өту құбылысы.
Жарық дифракциясының сфералық толқындар дифракциясы (Френель дифракциясы) және параллель сәулелер дифракциясы (Фраунгофер дифракциясы) деп аталатын екі түрі бар.Құбылысты 17 ғ-да италиялық физик және астроном Ф.Гримальди (1618 — 1663) ашты, ал оны француз физигі О.Френель (1788 — 1827) түсіндірді (1812). Френель Жарық дифракциясын екінші реттік толқындардың интерференциялану нәтижесі деп тұжырымдады. Зоналар (аймақтар) әдісі деп аталатын бұл көрнекі әдіс бойынша толқындық бет ойша дөңгелек аймақтарға бөлінеді. Осы аймақтардан таралып бір-біріне қабаттасуы кезінде интерференцияланған элементар толқындардың амплитудалары мен фазалары есепке алынады. Нүктелік жарық көзінен шыққан жарық, күңгірт экранның кішкене дөңгелек саңылауынан немесе күңгірт дөңгелек экранның шетінен өткенде, концентрлі шеңбер тәрізді дифракциялық жолақтар пайда болды.
ДАПТЕР ФОРМУЛА КЫСКАША
34. Құйынды электр өрісі. Ығысу тогы. Толық ток тығыздығы.
Құйынды электр өрісін уақыт бойынша өзгеретін магнит өрісі тудырады. Өрісте бірлік оң зарядты тұйық контур бойымен орын ауыстырғанда атқарылған жұмыс нөлге тең емес, ол индукцияның ЭҚК-не тең
 , (2.1)
, (2.1)
мұндағы  - айнымалы магнит өрісімен индукцияланған электр өрісінің кернеулігі. Электрмагниттік индукция заңынан (1.1),
- айнымалы магнит өрісімен индукцияланған электр өрісінің кернеулігі. Электрмагниттік индукция заңынан (1.1),

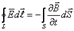 Максвелл теориясының бірінші тұжырымы: магнит өрісінің кез-келген өзгерісі құйынды электр өрісін тудырады.
Максвелл теориясының бірінші тұжырымы: магнит өрісінің кез-келген өзгерісі құйынды электр өрісін тудырады.
Айнымалы электр өрісінің «магниттік әсерінің» сандық түрде сипаттау үшін ығысу тогыдеген ұғым енгізілді.
конденсаторда өткізгіштік токты тұйықтайтын қандай да бір процесс өтеді, бұл – ығысу тогы. Айнымалы ток тізбегінде конденсатор астарлары
арасында кернеулігі  электр өрісі бар. Бұл формулада
электр өрісі бар. Бұл формулада  - астардағы зарядтың беттік тығыздығы,
- астардағы зарядтың беттік тығыздығы,  - астарлар арасындағы заттың диэлектрік өтімділігі. Заряды
- астарлар арасындағы заттың диэлектрік өтімділігі. Заряды 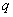 және пластиналардың ауданы
және пластиналардың ауданы  конденсатор астарлары арасындағы электр ығысуы
конденсатор астарлары арасындағы электр ығысуы 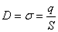 Тізбектегі ток күші
Тізбектегі ток күші  , бұдан
, бұдан
 , (2.4)
, (2.4)
яғни конденсатор астарлары арасындағы электр ығысуының өзгеру жылдамдығы тізбектегі токты тұйықтайтын процесс болып табылады. Онда астарлар арасындағы кеңістіктегі ығысу тогының тығыздығы
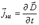 . (2.5)
. (2.5)
Максвелдің теориясына сәйкес (екінші тұжырымы), ығысу тогы өткізгіштік ток сияқты құйынды магнит өрісінің көзі болып табылады. Максвелдің екінші теңдеуін мына түрде жазуға болады
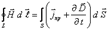 , (2.6)
, (2.6)
мұндағы  - толық ток тығыздығы.
- толық ток тығыздығы.
(2.6) теңдеу электромагниттік өріске ойша енгізілген кез-келген қозғалмайтын тұйық контур бойынша алынған  магнит өрісінің кернеулік векторының циркуляциясы
магнит өрісінің кернеулік векторының циркуляциясы  беттен өтетін өткізгіштік және ығысу токтарының алгебралық қосындысына тең болатынын көрсетеді.
беттен өтетін өткізгіштік және ығысу токтарының алгебралық қосындысына тең болатынын көрсетеді.
35.Бір саңылаудағы дифракция. Дифракциялық тор. Кеңістіктік тор. Голография.
Жарық дифракциясы — жарық толқындарының мөлшері сол толқындардың ұзындығымен қарайлас тосқауылды (тар саңылау, жіңішке сым, т.б.) орап өту құбылысы. Δ=dsinφ. Δ-жол айырым. Дифракциялық тoр дегеніміз — жарық дифракциясы байқалатын тосқауылдар және саңылаулардың жиынтығы. Геометриялық құрылысына қарай торларды жазық және кеңістіктік торлар деп те бөледі. Кеңістіктік реттелмеген торларға, мысалы, тұмандағы ауа тамшылары немесе мұз қиыршықтарының жиынтығы, көз кірпіктері жатады.
Саңылаудың ені а, ал тосқауыл-штрихтің ені b болсын, сонда b + a = d тордың тұрақтысы немесе периоды деп аталады.  штрихтар саны, l-тор өлшемі,d периоды.Минимум болу шарты:
штрихтар саны, l-тор өлшемі,d периоды.Минимум болу шарты:  , максимум болу шарты
, максимум болу шарты  .
.
Голография-интерференциялық көріністерді толық жазып және оны қалпына келтіретін ерекше тәсіл.Интерференция құбылысына негізделгесін қабаттасқан толқындар когерентті болу керек.Денелік толқын мен тірек толқынның фотопластинкаға жазылып алынған интерференциялық суреті голограмма деп аталады.
36.Электромагниттік энергия ағынының тығыздығы. Пойнтинг векторы. Дипольдің сәуле шығаруы.
Энергия тасымалы электрмагниттік толқынмен байланысты. Изотропты ортада электрмагниттік өріс энергиясының тығыздығы электр және магнит өрістерінің энергия тығыздықтарының суммасына тең:

E және H векторларының байланысын ескерсек, электрмагниттік толқынның энергиясының көлемдік тығыздығы

мұндағы – v толқынның жылдамдығы (6.4). (6.6) өрнекті жылдамдыққа көбейтсек, энергия ағыны тығыздығын аламыз:

E мен H векторлары өзара перпендикуляр және бағыттары оң бұрандалы жүйе таралу бағытына сәйкес (6.1-сурет), сондықтан (6.7) теңдеу мына түрде жазылады.

S векторы Пойнтинг векторы деп аталады.ол электрмагниттік толқынның таралу бағытымен бағыттас, ал модулі электрмагниттік толқынның таралу бағытына перпендикуляр бірлік аудан арқылы тасымалданатын энергияға тең.
Гармоникалық электрмагниттік қума толқын үшін энергия ағынының тығыздығы:

Толқын интенсивтілігі I энергия ағынының тығыздығының орташа мәніне тең:

(6.9) өйткені косинустың квадратының орташа мәні ½-ге тең.
Дипольдің сәуле шығаруы.
Электромагниттік толқынды үдемелі қозғалатын зарядталған бөлшектер шығарады
 - дипольдікмомент, электр моменті;
- дипольдікмомент, электр моменті;  =
=  const;p0=ql- max мәні
const;p0=ql- max мәні
37. Жарық поляризациясы. Екі диэлектрик ортаның шекарасындағы жарықтын шағылу мен сыну кезіндегі поляризация.
Қандай да бір жағдай жасалып, жарық векторы бір бағытта ғана тербелетін болса, ол поляризацияланған жарық деп аталады.Жарық поляризациясын сипаттау үшін поляризацилану дәрежесі деген шама енгізейік  , мұндағы
, мұндағы 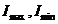 , - жарық интенсивтілігінің максимум және минимум мәндері.
, - жарық интенсивтілігінің максимум және минимум мәндері.
Егер жарықты екі поляризатордан қатар өткізсе, онда өткен жарықтың интенсивтілігі Малюс заңынан анықталады  ,мұндағы
,мұндағы  - екі поляризатор арасындағы бұрыш.
- екі поляризатор арасындағы бұрыш.
Екі орта шекарасына түскен жарық, шағылу немесе сыну кезінде өзінің поляризациясын өзгертеді. Түсу бұрышы нөлден өзгеше болса, шағылған және сынған сәулелер жартылай поляризацияланады. Шағылған жарықтың электр өрісінің кернеулік векторы түсу жазықтығына перпендикуляр жазықтықта, ал сынған жарықтікі – параллелль жазықтықта тербеледі. Белгілі бір  бұрышта ғана (Брюстер бұрышы)
бұрышта ғана (Брюстер бұрышы)
 шағылған жарық толығымен поляризацияланады.
шағылған жарық толығымен поляризацияланады.
38. Фотондар. Жарық кванттарының энергиясы және импульсы. Жарық қысымы.
Фотондар- электомагниттік сәуленің кванты. Жарық сәулесінің энергиясының шығарылып (жұтылуы) Фотонның энергиясы  , Массасы. Эйнштейн формуласынан
, Массасы. Эйнштейн формуласынан  ,
,  бұдан
бұдан  Импульсі
Импульсі  . Векторлық түрде
. Векторлық түрде 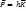 бұдан импульстің бағыты электромагнит сәулесінің таралу бағытымен сәйкес келеді, мұндағы K- толқындық сан. Фотонның тыныштық массасы
бұдан импульстің бағыты электромагнит сәулесінің таралу бағытымен сәйкес келеді, мұндағы K- толқындық сан. Фотонның тыныштық массасы  . Олай болса энергия мен импульстің арасындағы қатынас
. Олай болса энергия мен импульстің арасындағы қатынас 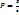 . Тыныштық массасы нөлге тең болғандықтан, тек қозғалыста өмір сүре алады. Жарық қысымы — жарықтың жұтылу не шағылу процестері кезінде денеге фотондар (электрмагниттік өріс энергиясының кванттары) импульсінің берілу нәтижесі.
. Тыныштық массасы нөлге тең болғандықтан, тек қозғалыста өмір сүре алады. Жарық қысымы — жарықтың жұтылу не шағылу процестері кезінде денеге фотондар (электрмагниттік өріс энергиясының кванттары) импульсінің берілу нәтижесі.
39. Жылулық сәуле шығару. Жылулық сәуле шығару заңдары. Абсалют қара дененің сәуле шығару проблемалары. Планк формуласы және кванттық гипотезасы .
Жылулық сәуле шығару-дененің ішкі энергиясының электро-магнитті толқын түрінде таралуы. Температурасы абсолюттік нольден жоғары кез келген агрегаттық күйдегі барлық денелер жылулық сәуле шығарады. Жылулық сәуле шығару интенсивтілігі мен оның спетрлік құрамы сәуле шығаратын дененің оптикалық қасиеттері мен температурасына тәуелді.
ДАПТЕР ФОРМУЛА КЫСКАША
Планк формуласы. Берілген формула толқын жиілігінің 0-ден  -ке дейінгі аралықта тәжірибе нәтижесімен сәйкес келеді. Планк формуласының физикалық мағынасы. Планк формуласына энергия тығыздығы жиіліктің кіші ж/е үлкен мәндерінде нөлге ұмтылады ж/е дененің температурасы өскен кезде энергия максимумы жиіліктің өсу жағына ұмтылады. Бұлай болу себебі Планк формуласы екі көбейткіштен тұрады
-ке дейінгі аралықта тәжірибе нәтижесімен сәйкес келеді. Планк формуласының физикалық мағынасы. Планк формуласына энергия тығыздығы жиіліктің кіші ж/е үлкен мәндерінде нөлге ұмтылады ж/е дененің температурасы өскен кезде энергия максимумы жиіліктің өсу жағына ұмтылады. Бұлай болу себебі Планк формуласы екі көбейткіштен тұрады  ж/е
ж/е 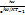 .
.
40. Ядроның байланыс энергиясы. Массалық ақау.
Дәл өлшеулер бойынша ядроның мя массасы ондағы нуклондардың массаларының қосындысынан әрқашанда кіші болатыны шығады
Мя<Zmp+Nmn
Ядродағы нуклондардың массаларының қосындысынан оның массасының айырымы массалық ақау деп аталады. Массалық ақау:  , Массалық ақау ядродағы нуклондардың байланыс энергиясын сипаттайды. Байланыс энергиясы – ядроның оны құрайтын нуклондарға ыдыратуға кететін Wбайл минимал энергия. Байланыс энергиясы ядроның беріктігін сипаттайтын негізгі шамалардың бірі. Ядроның байланыс энергиясын біле отырып, кез келген ыдырау және ядролардың өзара түрлену процесстері үшін энергетикалық шығыстарды есептеуге болады. Эйнштейн формуласымен анықталады.
, Массалық ақау ядродағы нуклондардың байланыс энергиясын сипаттайды. Байланыс энергиясы – ядроның оны құрайтын нуклондарға ыдыратуға кететін Wбайл минимал энергия. Байланыс энергиясы ядроның беріктігін сипаттайтын негізгі шамалардың бірі. Ядроның байланыс энергиясын біле отырып, кез келген ыдырау және ядролардың өзара түрлену процесстері үшін энергетикалық шығыстарды есептеуге болады. Эйнштейн формуласымен анықталады.
Ядроның байланыс энергиясы:  .
.
мұндағы ma– атом массасы;
mn– сутегі атомының массасы.
Байланыс энерсиясының А толық нуклондар санына қатынасы меншікті байланыс энергиясы деп аталады. Em.б=Е/А.
41. Жылулық сәуле шығару. Стефан –Больцман және Вин заңдары
Жылулық сәуле шығару – дененің ішкі энергиясының электромагниттік толқын түрінде шығарады. Дене кез келген температурада жылулық сәуле шығарады. Термодинамикалық тепе теңдік күйде болатын дененің электромагниттік сәуле шығаруы. Тепе теңдік күй сақталу үшін дененің сәуле шығару нәтижесінде энергия қанша кемісе, жұтылатын энергия мөлшері де сондай болуға тиіс.
Энергетикалық жарқырау дененің бетінен бірлік уақытта шығарылатын сәулелік энергия. Энергетикалық жарқыраушы температураға тәуелді. Сәулелену әр түрлі жиіліктен түрады, олай болса спектрлік сәуле шығарғыштық қабілеті деген физикалық шама енгізіледі.
r=  - спектрлік аралықтық бір алқабына келетін дененің бірлік ауданынан шығатын сәуленің қуаты. Энергетикалық жарқырау R=
- спектрлік аралықтық бір алқабына келетін дененің бірлік ауданынан шығатын сәуленің қуаты. Энергетикалық жарқырау R= 
Сәуле жұтқыштық қабілеті -  жұтылған энергияның түскен энергияға қатынасы.
жұтылған энергияның түскен энергияға қатынасы.
Спектрлік сәуле жұтқыштық қабілеті – толқындар жиілігі v және v+dv аралығындағы сәулелер энергиясының белгілі температурада дененің беті жұтқыш бөлігін көрсететін шама. Абсолют қара дене – дене бетіне түскен энергияны толығымен жұтатын дене.
Стефан больцман заңы: абсолют қара дененің толық жарқырауы оның төрт дәрежеленген абсолют температурасына пропорционал – R= 
Вин заңы 1) абсолют қара дененің спектрлік сәуле шығарғыштық қабілетінің максимал мәніне келетін жиілік оның температурасына тура пропорционал. Vmax =BT немесе толқын ұзындығы арқылы  м*К
м*К
2) Абсолют қара дененің энергетикалық жарқырауының максимал спектрлңк тығыздығы бесінші дәрежелі абсолют температураға пропорционал өседі r=bT5
42. Электромагниттік толқын энергиясы. Энергия ағынының тығыздығы. Пойнтинг векторы. . Электромагниттік толқын импульсі.
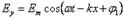 Максвелл теориясы бойынша (2,3), айнымалы магнит өрісі айнымалы электр өрісін тудырады және керісінше. Егер кеңістіктің белгілі бір нүктесінде құйынды электр өрісін тудырсақ, онда қоршаған ортада электр және магнит өрістерінің өзара айналымы пайда болады, яғни электрмагниттік өріс уақыт пен кеңістік бойынша таралады. Бұл процесс периодты және электрмагниттік толқын деп аталады.
Максвелл теориясы бойынша (2,3), айнымалы магнит өрісі айнымалы электр өрісін тудырады және керісінше. Егер кеңістіктің белгілі бір нүктесінде құйынды электр өрісін тудырсақ, онда қоршаған ортада электр және магнит өрістерінің өзара айналымы пайда болады, яғни электрмагниттік өріс уақыт пен кеңістік бойынша таралады. Бұл процесс периодты және электрмагниттік толқын деп аталады.

Электрмагниттік өрістің әрбір нүктесінде E және H векторлары бірдей жиілікпен гармоникалық тербеледі. Сондықтан электрмагниттік толқын монохроматтыболып табылады.
Энергия тасымалы электрмагниттік толқынмен байланысты. Изотропты ортада электрмагниттік өріс энергиясының тығыздығы электр және магнит өрістерінің энергия тығыздықтарының суммасына тең:

E және H векторларының байланысын ескерсек, электрмагниттік толқынның энергиясының көлемдік тығыздығы

мұндағы – v толқынның жылдамдығы (6.4). (6.6) өрнекті жылдамдыққа көбейтсек, энергия ағыны тығыздығын аламыз:

E мен H векторлары өзара перпендикуляр және бағыттары оң бұрандалы жүйе таралу бағытына сәйкес (6.1-сурет), сондықтан (6.7) теңдеу мына түрде жазылады.

S векторы Пойнтинг векторы деп аталады.ол электрмагниттік толқынның таралу бағытымен бағыттас, ал модулі электрмагниттік толқынның таралу бағытына перпендикуляр бірлік аудан арқылы тасымалданатын энергияға тең.
Гармоникалық электрмагниттік қума толқын үшін энергия ағынының тығыздығы:
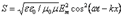
Толқын интенсивтілігі I энергия ағынының тығыздығының орташа мәніне тең:

(6.9) өйткені косинустың квадратының орташа мәні ½-ге тең.
43.Заттардың корпускулалық-толқындық дуализмді. Гейзенбергтің анықталмағандық қатынастары.
Жарық нақты физикалық объект болып табылады. Жарықты кейбір жағдайларда бөлшек түрінде қарастыруға болады, ал басқа жағдайларда толқын түрінде қарастыруға болады.Физикалық объект бір мезгілде корпускулалық және толқындық қасиеттерге ие болса, онда мұны корпускулалық-толқындық дуализмі деп атайды.Корпускулалық-толқындық дуализмді классикалық ұғымдармен түсіндіре алмаймыз, себебі фотонды әрбір уақыт мезетінде кеңістікте белгілі бір орын алатын нүктелік объект деп қарастыруға болмайды. Жеке фотонды электр өрісінің кернеулігімен сипаттауға болмайды.Фотон дегеніміз – электромагниттік сәуле шығарумен байланыста болатын физикалық объект, ол энергиямен және импульспен сипатталады.
Классикалық физикада бөлшек пен толқынның табиғатын әртүрлі деп қарастырады. Бөлшек дискретті, кеңістікте өте аз көлем алады, ал толқын болса кеңістікте өте үлкен орын алады.
Толқын бір ортадан екінші ортаға өткенде жартылай сынып, екінші ортада тарлады, ал жартысы шағылып, интерференциаланады. Бөлшек болса біртұтас, ол интерференциаланбайды.
Бірақ ХІХ ғ. 20-жылдарында физикада табиғаттың фундаментальды заңы ашылды, ол заттың корпускулалық-толқындық дуализмі деп аталады, мұнда бөлшек пен толқын туралы түсініктер біріктірілді.
Гейзенбергтің анықталмағандық қатынасы.
Гейзенбергтің анықталмағандық қатынасы – бөлшектің координатасы мен импульсінің бір уақытта анықтау мүмкін еместігі туралы принцип. Ол бойынша  түрде болады.
түрде болады.
Классикалық механикада кез келген бөлшек белгілі бір траекториямен қозғалатын болса, онда кез келген уақыт мезетінде оның координатасы мен импульсін анықтауға болады. Классикалық бөлшектен айырмашылығы микробөлшектердің толқындық қасиеттері бар екенінде. Негізгі айырмашылығы микробөлшектердің траекториясы хаостық, ал оның координатасы мен импульсінің дәл мәнін анықтау мүмкін емес.
Бұл корпускулалық-толқындық дуализмнен шығады. Мысалы, бір нүктедегі толқын ұзындығы деп айтуға болмайды, оның физикалық мағынасы жоқ, ал импульс толқын ұзындығына тәуелді шама, осыдан, микробөлшектің импульсі белгілі болса, координатасы белгісіз және керісінше, микробөлшектерінің координатасының дәл мәні белгілі болса, онда оның импульсі белгісіз болады.
Мысалы, электрон үшін координата  мен импульс компонентінің
мен импульс компонентінің  дәл мәнін анықтау мүмкін емес.
дәл мәнін анықтау мүмкін емес.  пен
пен  анықталмағандықтары төмендегі қатынасты қанағаттандырады
анықталмағандықтары төмендегі қатынасты қанағаттандырады
 . (10.3)
. (10.3)
Аналогиялық түрде (10.3) қатынасын  пен
пен  ,
,  пен
пен  үшін де және энергия мен уақыт үшін де жазуға болады
үшін де және энергия мен уақыт үшін де жазуға болады
 . (10.4)
. (10.4)
(10.3) и (10.4) қатынастары анықталмағандық қатынастары деп аталады. Анықталмағандақ қатынастарын бірінші рет 1927 ж. В.Гейзенберг орнатты.
Бұл қатынастардың физикалық мағынасы төмендегідей: микроәлем объектісі координаталары мен импульс проекцияларының дәл мәні анықталатын күйде бола алмайды.
(10.4) формулаға сәкес энергияны  дәлдікпен өлшеу үшін
дәлдікпен өлшеу үшін 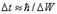 уақыт қажет. Мысал ретінде сутегітектес атомдардың энергетикалық деңгейлерінің (негізгі деңгейден басқа деңгейлер) дәл мәнінің болмауын келтіруге болады. Бұл спектрлік сызықтардың кеңеюіне әкеліп соғады және оны барлық қозған күйдегі өмір сүру
уақыт қажет. Мысал ретінде сутегітектес атомдардың энергетикалық деңгейлерінің (негізгі деңгейден басқа деңгейлер) дәл мәнінің болмауын келтіруге болады. Бұл спектрлік сызықтардың кеңеюіне әкеліп соғады және оны барлық қозған күйдегі өмір сүру 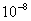 с уақытымен түсіндіруге болады. Сонымен бірге, егер жүйе тұрақты болмаса (радиоактивті ядро), онда өмір сүру уақытының шекті болуына байланысты оның энергиясы
с уақытымен түсіндіруге болады. Сонымен бірге, егер жүйе тұрақты болмаса (радиоактивті ядро), онда өмір сүру уақытының шекті болуына байланысты оның энергиясы  -дан аз емес статистикалық дәлдікпен анықталады
-дан аз емес статистикалық дәлдікпен анықталады
 , (10.5)
, (10.5)
мұндағы  – жүйенің өмір сүру уақыты.
– жүйенің өмір сүру уақыты.
Мұндай сипаттама классикалық механикадағы бөлшек қозғалысының сипатттамаларынан өзгеше болады, себебі классикалық механикада бөлшек белгілі траекториямен қозғалады және әрбір нүктедегі координатасы мен импульсі белгілі. Екі түйіндес айнымалының анықталмағандық мәндерінің көбейтіндісі Планк ħ тұрақтысынан аз болмайды деген тұжырым Гейзенбергтің анықталмағандық принципі деп аталады.
Гейзенбергтің анықталмағандық принципі кванттық механикадағы фундаменталды қағидаларының бірі болып табылады және корпускулалық-толқындық дуализммен байланысты.
44. Гармоникалық осциллятор. Серіппелі маятник.
Гармоникалық осциляторлардегеніміз – екінші теңдеумен сипатталатын тербеліс жасайтын жүйе. 
Гарм осцилятор мысал ретінде: математикалық маятник, физикалық маятник, пружиналық маятник түрлерін жатқызуға болады.
Серіппелі маятник – абсолютті серпімді пружинаға ілінген массасы m жіп. Ол серпімді күш әсерінен гарм.терб. жа-ы: ma= -kx,  ,
, 
Тербелмелі контур (орыс. Колебательный контур) — сыйымдылығы С конденстордан және индуктивтілігі L катушкадан тұратын, сондай-ақ Ω0= 1/√( LC )периодты электр тербелісін туғызатын тұйық контур.
45. Механикалық тербеліс энергиялары. Кинетикалық потенциялдық және толық энергия.
Механикалық тербелістердің толық энергиясы кинетикалық және потенциалдық энергиялардың қосындысы арқылы анықталады

, және уақытқа тәуелділік графиктері 3.2 суретте көрсетілген.
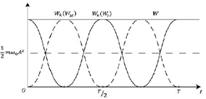
3.2 сурет
Тербелмелі контурда электромагниттік өрістің толық энергиясы . Конденсатордың зарядталуы кезінде оның астарларынынң арасында энергиясы электр өрісі пайда болады. Разрядталу кезінде индуктивті катушкада магнит өрісінің энергиясы пайда болады.
Магнит өрісінің энергиясы үшін
, (3.6) (3.6)
электр өрісінің энергиясы үшін
, (3.7)
және толық энергия
. (3.8)
46. Радиоактивті сәуле шығару және оның түрлері.
Радиоактивті құбылыс-атомдардың өздігінен сәуле шығаруы. Радиоактивті сәуле шығаратын заттар қасиеті радиоактивтілік деп аталады.Радиоактивтік элементтердің (уран,торий,радий т.б.) атомдары α,β,ϒ-сәулелерін шығара отырып, басқа бір элемент атомына айналады. Орнықсыз ядролардың белгілі уақыт аралығында орнықты күйге келіп үлгеретін шамасын көрсететін заңдылықты радиоактивтік заңдылықты радиоактивті ыдырау заңы атайды. Егер радиоактивтік ядроның алғашқы саны N0 болса, онда dt уақыт ішінде ыдырап үлгерген ядроның саны dN=-𝜆Ndt, мұндағы 𝜆-ыдырау тұрақтысы.  , бұдан N= N0
, бұдан N= N0  . Бұл радиоактивті ыдырау заңы. Радиоактивті ядролардың жартысы ыдырап үлгеретін уақытты жартылай ыдырау периоды деп атайды. N=
. Бұл радиоактивті ыдырау заңы. Радиоактивті ядролардың жартысы ыдырап үлгеретін уақытты жартылай ыдырау периоды деп атайды. N=  N0
N0 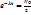 ,
,  бұдан ln2=𝜆t, T=
бұдан ln2=𝜆t, T=  =
=  .радиоактивті ядроның орташа өмір сүру уақыты
.радиоактивті ядроның орташа өмір сүру уақыты  ыдырау тұрақтысына кері шама. Радиоактивті ядроның активтігі A=
ыдырау тұрақтысына кері шама. Радиоактивті ядроның активтігі A=  .
.
Ығысу ережесі:  α-ыдырау үшін;
α-ыдырау үшін;
 β-ыдырау үшін;
β-ыдырау үшін;
α-бөлшек гелий ядросы, ыдырау формуласы 
β-бөлшек электрондар ағыны, ыдырау формуласы  . Бұдан басқа екі ыдырау түрі бар:
. Бұдан басқа екі ыдырау түрі бар:  p+
p+  →n+
→n+ 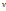 .
.
ϒ-бөлшек – электромагниттік толқын.
47.  -ыдырау және
-ыдырау және  -ыдырау. олардың заңдылықтары мен қасиеттері.
-ыдырау. олардың заңдылықтары мен қасиеттері.
 болып табылады. Заряды 2е, жылдамдығы (1,5-2)
болып табылады. Заряды 2е, жылдамдығы (1,5-2)  м/с. Энергиясы Е≈4-8 МэВ, ыдырауы формуласы
м/с. Энергиясы Е≈4-8 МэВ, ыдырауы формуласы  . Өтімділік қабілеті өте аз. Спектрлері дискретті. Ядродан шығатын
. Өтімділік қабілеті өте аз. Спектрлері дискретті. Ядродан шығатын  - бөлшек энергиясы жоғары потенциал тосқауылдан жарып өтеді.Бұл суретті тунелбдік эффектісі д.а.
- бөлшек энергиясы жоғары потенциал тосқауылдан жарып өтеді.Бұл суретті тунелбдік эффектісі д.а.
 - бөлшек ағыны.
- бөлшек ағыны.  - бөлшек электрондар ағыны. ʋ≈с. Энергиясы Е≈0,001-3 МэВ,ыдырау формуласы
- бөлшек электрондар ағыны. ʋ≈с. Энергиясы Е≈0,001-3 МэВ,ыдырау формуласы  Бета бөлшектің өтімділік қабілеті жоғары. Бұдан басқа екі ыдырау түрі бар:
Бета бөлшектің өтімділік қабілеті жоғары. Бұдан басқа екі ыдырау түрі бар:  p+
p+  →n+
→n+ 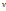 .
.
48 Еріксіз тербелістердің дифференциалды теңдеуі және оның шешімі.
Еріксіз тербелістер – периодты түрде өзгеретін күштің әсеріннен п.б. тербелістер. Диф.теңдеу:
x" + 2β x' +  2x =
2x =  . f(t) = f0coswt. Мұндағы, f0 –сырттан әсер ететін күштің амплитудасы, w-оның жиілігі,
. f(t) = f0coswt. Мұндағы, f0 –сырттан әсер ететін күштің амплитудасы, w-оның жиілігі,  - тербелістің меншікті жиілігі. Шешімі: x = acos(Ωt+ φ0).
- тербелістің меншікті жиілігі. Шешімі: x = acos(Ωt+ φ0).
Бұдан еріксіз тербеліс амплитудасы және тербелістің тепе-теңдіктен ығысуы мен сыртқы күштің арасындағы ығысу фазасы сыртқы күштің жиілігіне, меншікті жиілікке және өшу коэффициентіне байланысты.
49  -сәуле шығару және оның заңдылықтары мен қасиеттері.
-сәуле шығару және оның заңдылықтары мен қасиеттері.
 - бөлшектер ағыны.
- бөлшектер ағыны.  - жиілігі өте жоғары квант ағыны (λ(10^-10). Заряды жоқ. Спектрі сызықты. Энергиясы Е≈10КэВ-10 МэВ. Заттан өшу қабілеті жоғары. Ядроның қозыған күйден негізгі немесе одан төмен күйге өткендегі шығаратын электромагнит толқыны. Сонымен қатар ядролық реакция кезінде пайда болады. Жиілігі -ʋ=(Е1-Е2)/h;
- жиілігі өте жоғары квант ағыны (λ(10^-10). Заряды жоқ. Спектрі сызықты. Энергиясы Е≈10КэВ-10 МэВ. Заттан өшу қабілеті жоғары. Ядроның қозыған күйден негізгі немесе одан төмен күйге өткендегі шығаратын электромагнит толқыны. Сонымен қатар ядролық реакция кезінде пайда болады. Жиілігі -ʋ=(Е1-Е2)/h;  -сәулелері зат арқылы өткенде оның әрі электрондарымен, әрі ядросымен де өзара әсерлесе алады. Бұл сәулелер затпен әсерлескенде кванттық теоря б/ша фотоэффект, Комтпон эффектісі және электрон-позитрон жұптарын түзейтін процестері жүреді.
-сәулелері зат арқылы өткенде оның әрі электрондарымен, әрі ядросымен де өзара әсерлесе алады. Бұл сәулелер затпен әсерлескенде кванттық теоря б/ша фотоэффект, Комтпон эффектісі және электрон-позитрон жұптарын түзейтін процестері жүреді.
50 Электромагнитті сәуле шығарудың корпускулалы-толқындық дуализмі. Фотоэффект. Фотоэффектінің негізгі заңдары. Фотоэффект үшін Эйнштейн теңдеуі.
Фотоэффект дегеніміз – жарықтың әсерінен заттан электрондардың бөлініп шығу құбылысы. Заңдары: фотоэлектрондардың алғашқы максимал жылдамдығы фотокатодқа түскен жарықтың интенсивтілігіне байланысты болмай, жарық жиілігіне тәуелді. Бірлік уақыт ішінде катодтан бөлініп шыққан фотоэлектрондар саны жары интенсивтілігіне пропорционал. Кез келген заттың әліде болса фотоэффекті құбылысын қоздыра алатынжарық жиілігі фотоэффектінің қызыл шекарасы деп аталады.  . Фотоэффектінің үш түрі бар: ішкі, сыртқы, винтильді.
. Фотоэффектінің үш түрі бар: ішкі, сыртқы, винтильді.
Сыртқы фотоэффект (немесе фотоэлектронды эмиссией) деп электромагнитті сәулелену әсерінен электрондардың заттан ыршып шығу құбылысы. Ішкі фотоэффект деп – сәулелену әсерінен зат (сұйық немесе қатты жартылай өткізгіштер мен диэлектриктердегі) электрондардың энергетикалық деңгейлерде реттелуі, қайта орналасу құбылысы.
Вентильді фотоэффект – зат электронлары бір заттан екінші қатты затқа (жартылай өткізгіш) немесе сұйықтыққа (электролит) сәулелену әсерінен көшу құбылысы.
51 Жарық поляризациясы. Екі диэлектрик орта шекарасындағы жарықтың
шағылу, сыну кезіндегі поляризация.
Жарық көлденең электрмагниттік толқын болып табылады. Жарық толқынының векторы мүмкін болатын барлық бағытта тербелетін болса, мұндай жарық табиғи жарық деп аталады. Мысал ретінде күн сәулесін, электр шамының жарығын келтіруге болады.
Қандай да бір жағдай жасалып, жарық векторы бір бағытта ғана тербелетін болса, ол поляризацияланған жарық деп аталады. Поляризатор көмегімен табиғи жарықтан поляризацияланған жарықты алуға болады. Жарық поляризациясын сипаттау үшін поляризацилану дәрежесі деген шама енгізейік
 ,
,
мұндағы  , - жарық интенсивтілігінің максимум және минимум мәндері.
, - жарық интенсивтілігінің максимум және минимум мәндері.
Егер жарықты екі поляризатордан қатар өткізсе, онда өткен жарықтың интенсивтілігі Малюс заңынан анықталады
 ,
,
мұндағы 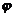 - екі поляризатор арасындағы бұрыш.
- екі поляризатор арасындағы бұрыш.
Екі орта шекарасына түскен жарық, шағылу немесе сыну кезінде өзінің поляризациясын өзгертеді. Түсу бұрышы нөлден өзгеше болса, шағылған және сынған сәулелер жартылай поляризацияланады. Шағылған жарықтың электр өрісінің кернеулік векторы түсу жазықтығына перпендикуляр жазықтықта, ал сынған жарықтікі – параллелль жазықтықта тербеледі. Белгілі бір  бұрышта ғана (Брюстер бұрышы)
бұрышта ғана (Брюстер бұрышы)

шағылған жарық толығымен поляризацияланады.
52. Құйынды электр өрісі. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы
Электрмагниттік индукция құбылысын оқып-үйрену кезінде айнымалы магнит өрісінде тыныштықта тұрған контурда индукциялық ток пайда болатыны байқалған. Оның пайда болу себебі бөгде күштердің әсері. Бұл күштердің табиғаты электростатикалық, магниттік емес және жылулық немесе химиялық процесстермен де байланысты емес. Максвелл магнит өрісінің кез келген өзгерісі қоршаған кеңістікте индукцияланған электр өрісін тудырады, бұл контурдағы индукциялық токтың туындау себебі болып саналады деген болжам айтты.
Электрстатикалық өрістен ерекшелігі индуцияланған электр өрісі потенциалды емес құйынды электр өрісі болып табылады, себебі осы өрісте бірлік оң зарядты тұйық контур бойымен орын ауыстырғанда атқарылған жұмыс нөлге тең емес, ол индукцияның ЭҚК-не тең
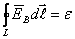 , (2.1)
, (2.1)
мұндағы  - айнымалы магнит өрісімен индукцияланған электр өрісінің кернеулігі.
- айнымалы магнит өрісімен индукцияланған электр өрісінің кернеулігі.
Электрмагниттік индукция заңынан (1.1),
 (2.2)
(2.2)
жазуға болады.
Жалпы жағдайда  электр өрісі электрстатикалық өріс және уақыт бойынша өзгеретін магнит өрісінің тудыратын өрісінің қосындысынан тұрады. Себебі, электрстатикалық өрістің циркуяциясы нөлге тең, (2.2) теңдеуді
электр өрісі электрстатикалық өріс және уақыт бойынша өзгеретін магнит өрісінің тудыратын өрісінің қосындысынан тұрады. Себебі, электрстатикалық өрістің циркуяциясы нөлге тең, (2.2) теңдеуді  өрісі осы екі өрістің векторлық қосындысынан тұратын жалпы өріс үшін келесі түрде жазуға
өрісі осы екі өрістің векторлық қосындысынан тұратын жалпы өріс үшін келесі түрде жазуға  болады
болады  . (2.3)
. (2.3)
Максвелдің бірінші теңдеуі (2.3) электромагниттік өріске ойша енгізілген кез-келген қозғалмайтын тұйық контур бойынша алынған  векторының циркуляциясы теріс таңбамен алынған
векторының циркуляциясы теріс таңбамен алынған  беттен өтетін магнит ағынының өзгеру жылдамдығына тең. Бұдан Максвелл теориясының бірінші тұжырымы: магнит өрісінің кез-келген өзгерісі құйынды электр өрісін тудырады.
беттен өтетін магнит ағынының өзгеру жылдамдығына тең. Бұдан Максвелл теориясының бірінші тұжырымы: магнит өрісінің кез-келген өзгерісі құйынды электр өрісін тудырады.
2.2 Ығысу тогыМаксвелл айнымалы электр өрісі электр тогы секілді магнит өрісінің көзі болады деп болжай келе, толық ток заңын толықтырды1. Айнымалы электр өрісінің «магниттік әсерінің» сандық түрде сипаттау үшін ығысу тогы деген ұғым енгізілді.
Тұрақты ток тізбегінде конденсатор үзіліс болып табылады, ал айнымалы токтың мұндай тізбекте өтетіндігі белгілі. Тізбектің барлық тізбектей жалғанған элементерінде де өткізгіштік квазистационар ток күші бірдей болады. Конденсаторда электрондардыңқозғалысымен байланысты өткізгіштік токтың болуы мүмкін емес, себебі конденсатор астарларының арасы диэлектрикпен толтырылған. Бұдан шығатын қорытынды, конденсаторда өткізгіштік токты тұйықтайтын қандай да бір процесс өтеді, бұл – ығысу тогы. Айнымалы ток тізбегінде (2.1 суретті қара) конденсатор астарлары
2.1 сурет арасында кернеулігі  электр өрісі
электр өрісі
бар. Бұл формулада  - астардағы зарядтың беттік тығыздығы,
- астардағы зарядтың беттік тығыздығы,  - астарлар арасындағы заттың диэлектрік өтімділігі.
- астарлар арасындағы заттың диэлектрік өтімділігі.
Заряды 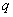 және пластиналардың ауданы
және пластиналардың ауданы  конденсатор астарлары арасындағы электр ығысуы
конденсатор астарлары арасындағы электр ығысуы  .
.
Тізбектегі ток күші  , бұдан
, бұдан
 , (2.4)
, (2.4)
яғни конденсатор астарлары арасындағы электр ығысуының өзгеру жылдамдығы тізбектегі токты тұйықтайтын процесс болып табылады. Онда астарлар арасындағы кеңістіктегі ығысу тогының тығыздығы
 . (2.5)
. (2.5)
Максвелдің теориясына сәйкес (екінші тұжырымы), ығысу тогы өткізгіштік ток сияқты құйынды магнит өрісінің көзі болып табылады (2.1 суретті қара).
Максвелдің екінші теңдеуін мына түрде жазуға болады
 , (2.6)
, (2.6)
мұндағы  - толық ток тығыздығы.
- толық ток тығыздығы.
(2.6) теңдеу электромагниттік өріске ойша енгізілген кез-келген қозғалмайтын тұйық контур бойынша алынған  магнит өрісінің кернеулік векторының циркуляциясы
магнит өрісінің кернеулік векторының циркуляциясы  беттен өтетін өткізгіштік және ығысу токтарының алгебралық қосындысына тең болатынын көрсетеді.
беттен өтетін өткізгіштік және ығысу токтарының алгебралық қосындысына тең болатынын көрсетеді.
2.3 Максвелл теңдеулерінің жүйесі
Максвелл теңдеулерінің жүйесі 2.1 кестеде көрсетілген.
2.1 кесте
| Интегралдық түрі | Дифференциалдық түрі |
1. 
| 
|
2. 
| 
|
3. 
| 
|
4. 
| 
|
| 5. 6. 7. | |
Алғашқы екі теңдеуден маңызды қорытынды шығады: айнымалы электр және магнит өрістері біртұтас электромагниттік өріс жасап, бір-бірімен тығыз байланысқан.
Үшінші және төртінші теңдеулер электр өрісінің көздері – электр зарядтары, ал магниттік зарядтардың болмайтынын көрсетеді. Сондықтан Максвелл теңдеулері электр және магнит өрістеріне қатысты симметриялы емес. 2.1 кестеде (5,6,7) қатынастары материялық теңдеулер деп аталады, себебі олар ортаның жеке қасиеттерін көрсетеді.
Максвелл теориясы сол кездегі белгілі барлық тәжірибелік фактілерді түсіндірді және бірқатар жаңа құбылыстарды болжады. Оның теориясының негізгі салдары жарық жылдамдығымен таралатын электромагниттік толқындардың болуы жөнінде қорытынды болды, ол кейіннен жарықтың электромагниттік теориясын құруға алып келді.
1. Электромагниттік индукция құбылысы. Фарадей заңы және оны энергияның сақталу заңынан қорытып шығару. Ленц ережесі.
2. Ядроның байланыс энергиясы. Ядроның бөліну реакциясы. Энергия көздерінің мәселелері.
3. Өздік және өзара идукция құбылыстары. Индуктивтілік.
Токтың магнит энергиясы. Магнит өрісінің энергиясының көлемдік тығыздығы.
4. Радиоактивтілік. Радиоактивті ыдырау заңы. Ыдырау түрлері мен заңдылықтары.
5.Электромагниттік өріс үшін Максвелл теориясының жалпылама сипаттамасы. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы
6. Атом ядросы. Атом ядросының құрылысы және негізгі қасиеттері. Ядролық күштер.
7.Электр тізбегін тұйықтау және ажырату кезіндегі экстратоктар.
8. Элементар бөлшектер. Фундаментальды әсерлесулер.
9. Тербелмелі процестер. Гармоникалық тебелістердің жалпы сипаттамалары.
10. Металдар мен жартылай өткізгіштердегі түйіспелі құбылысы ( Зеебек, Пелтье құбылыстары). Электронды- кемтікті байланыс (p-n-ауысу).Жартылай өткізгішті диод
11.Гармоникалық механикалық тебелістердің дифференциалды теңдеуі. Гармоникалық осцилляторлар.Физикалық маятник.
12. Жүйенің химиялық потенциалы (Ферми деңгейі). Металдардағы электронды өткізгіштік. Металдардың электр өткізгіштігі. Асқын өткізгіштік. Асқын өткізгіштікті ғылым мен техникада қолдану.
13.Гармоникалық электр тебелістерінің дифференциалды теңдеуі. Гармоникалық электр тербелістерінің энергиясы. Тербелмелі контур.
14. Қатты денелердің аумақтық теориясы. Аймақтық теориядағы металдар, өткізгіштер мен
15. Бір бағыттағы тербелістерді қосу. Векторлық диаграмма. Соғу.
16. Кванттық статистика элементтері.Фазалық кеңістік. Таралу функциялары. Ферми – Дирак және Бозе-Эйнштейн кванттық статистикалары туралы түсінік. Бозондар және фермиондар.
17. Еркін өшетін тербелістер және оның сипаттамалары. Өшу коффициенті, өшудің логарифмдік декременті. Сапалылық.
18. Электромагниттік сәуле шығарудың затпен өзара әсерлесуінің кванттық табиғаты. Спонтанды және еріксіз сәуле шығарулар. Лазер.
19. Еріксіз тербелістер. Еріксіз тербеліс фазасы және амплитудасы. Резонанстық қисықтар.
20 Кванттық гармоникалық осциллятор. Нөлдік энергия. Бөлшектердің потенциалды тосқауыл арқылы өтуі.
21. Шексіз терең қабырғалы бір өлшемді тік бұрышты потенциалды шұңқырдағы бөлшектер. Бордың сәйкестік принціптері.
22. Толқындық қозғалыстың негізгі сипаттамалары.. Сфералық және жазық толқын. Толқын теңдеуі. Фазалық жылдамдық. Топтық жылдамдық. Толқындық теңдеу.
23.Шредингердің уақыттық және стационар теңдеуі. Қарапайым кванттық жүйе үшін Шредингер теңдеуінің шешімі. Бордың сәйкестік принципі.
24. Серпінді толқын энергиясы. Энергия ағынының тығыздығы.. Умов векторы
25. Толқындардың суперпозиция принціпі. Топтық жылдамдық пен фазалық жылдамдық және олардың арасындағы байланыс. Толқындардың интерференциясы.
26.Сутегі атомы үшін Шредингер теңдеуі. Энергетикалық деңгейлер. Деңгей ені. Спин.Кеңістіктің квантталуы. Паули принципі.
27. Кванттық механикадағы микробөлшектердің күйі. Толқындық функция және оның статистикалық мағынасы. Шредингердің уақыттық және стационар теңдеуі
28. Электромагниттік өріс үшін толқын теңдеу. Толқындық теңдеу. Электромагнитті толқын қасиеттері.
29.Жарық толқыны және оның сипаттамалары. Жарықтың монохраматтылығы және когеренттілігі. Жарық жылдамдығын анықтау тәжерибелері.
30. Заттардың корпускулалық-толқындық дуализмді. Де Бройль гипотезасы және оны тәжерибелермен растау. Де Бройль толқынының қасиеттері.
31.Жарық интерференциясы және оны бақылау тәсілдері.
32. Комптон эффектісі және оның элементар теориясы.
33. Жарыққ дифракциясы. Гюгенс-Френель принціпі. Френельдің зоналар әдісі.
34. Құйынды электр өрісі. Ығысу тогы. Толық ток тығыздығы.
35.Бір саңылаудағы дифракция. Дифракциялық тор. Кеңістіктік тор. Голография.
36.Электромагниттік энергия ағынының тығыздығы. Пойнтинг векторы. Дипольдің сәуле шығаруы.
37. Жарық поляризациясы. Екі диэлектрик ортаның шекарасындағы жарықтын шағылу мен сыну кезіндегі поляризация.
38. Фотондар. Жарық кванттарының энергиясы және импульсы. Жарық қысымы.
39. Жылулық сәуле шығару. Жылулық сәуле шығару заңдары. Абсалют қара дененің сәуле шығару проблемалары. Планк формуласы және кванттық гипотезасы .
40. Ядроның байланыс Энергиясы. Массалық ақау.
41. Жылулық сәуле шығару. Стефан –Больцман және Вин заңдары..
42. Электромагниттік толқын энергиясы. Энергия ағынының тығыздығы. Пойнтинг векторы. . Электромагниттік толқын импульсі.
43.Заттардың корпускулалық-толқындық дуализмді. Гейзенбергтің анықталмағандық қатынастары.
44. Гармоникалық осциллятор. Серіппелі маятник.
45. Механикалық тербеліс энергиялары. Кинетикалық потенциялдық және толық энергия.
46. Радиоактивті сәуле шығару және оның түрлері.
47. 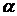 -ыдырау және
-ыдырау және  -ыдырау. олардың заңдылықтары мен қасиеттері.
-ыдырау. олардың заңдылықтары мен қасиеттері.
48 Еріксіз тербелістердің дифференциалды теңдеуі және оның шешімі.
49  -сәуле шығару және оның заңдылықтары мен қасиеттері.
-сәуле шығару және оның заңдылықтары мен қасиеттері.
50 Электромагнитті сәуле шығарудың корпускулалы-толқындық дуализмі. Фотоэффект. Фотоэффектінің негізгі заңдары. Фотоэффект үшін Эйнштейн теңдеуі.
51 Жарық поляризациясы. Екі диэлектрик орта шекарасындағы жарықтың
шағылу, сыну кезіндегі поляризация.
52. Құйынды электр өрісі. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы
1. Электромагниттік индукция құбылысы. Фарадей заңы және оны энергияның сақталу заңынан қорытып шығару. Ленц ережесі.
2. Ядроның байланыс энергиясы. Ядроның бөліну реакциясы. Энергия көздерінің мәселелері.
3. Өздік және өзара идукция құбылыстары. Индуктивтілік.
Токтың магнит энергиясы. Магнит өрісінің энергиясының көлемдік тығыздығы.
4. Радиоактивтілік. Радиоактивті ыдырау заңы. Ыдырау түрлері мен заңдылықтары.
5.Электромагниттік өріс үшін Максвелл теориясының жалпылама сипаттамасы. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы
6. Атом ядросы. Атом ядросының құрылысы және негізгі қасиеттері. Ядролық күштер.
7.Электр тізбегін тұйықтау және ажырату кезіндегі экстратоктар.
8. Элементар бөлшектер. Фундаментальды әсерлесулер.
9. Тербелмелі процестер. Гармоникалық тебелістердің жалпы сипаттамалары.
10. Металдар мен жартылай өткізгіштердегі түйіспелі құбылысы ( Зеебек, Пелтье құбылыстары). Электронды- кемтікті байланыс (p-n-ауысу).Жартылай өткізгішті диод
11.Гармоникалық механикалық тебелістердің дифференциалды теңдеуі. Гармоникалық осцилляторлар.Физикалық маятник.
12. Жүйенің химиялық потенциалы (Ферми деңгейі). Металдардағы электронды өткізгіштік. Металдардың электр өткізгіштігі. Асқын өткізгіштік. Асқын өткізгіштікті ғылым мен техникада қолдану.
13.Гармоникалық электр тебелістерінің дифференциалды теңдеуі. Гармоникалық электр тербелістерінің энергиясы. Тербелмелі контур.
14. Қатты денелердің аумақтық теориясы. Аймақтық теориядағы металдар, өткізгіштер мен
15. Бір бағыттағы тербелістерді қосу. Векторлық диаграмма. Соғу.
16. Кванттық статистика элементтері.Фазалық кеңістік. Таралу функциялары. Ферми – Дирак және Бозе-Эйнштейн кванттық статистикалары туралы түсінік. Бозондар және фермиондар.
17. Еркін өшетін тербелістер және оның сипаттамалары. Өшу коффициенті, өшудің логарифмдік декременті. Сапалылық.
18. Электромагниттік сәуле шығарудың затпен өзара әсерлесуінің кванттық табиғаты. Спонтанды және еріксіз сәуле шығарулар. Лазер.
19. Еріксіз тербелістер. Еріксіз тербеліс фазасы және амплитудасы. Резонанстық қисықтар.
20 Кванттық гармоникалық осциллятор. Нөлдік энергия. Бөлшектердің потенциалды тосқауыл арқылы өтуі.
21. Шексіз терең қабырғалы бір өлшемді тік бұрышты потенциалды шұңқырдағы бөлшектер. Бордың сәйкестік принціптері.
22. Толқындық қозғалыстың негізгі сипаттамалары.. Сфералық және жазық толқын. Толқын теңдеуі. Фазалық жылдамдық. Топтық жылдамдық. Толқындық теңдеу.
23.Шредингердің уақыттық және стационар теңдеуі. Қарапайым кванттық жүйе үшін Шредингер теңдеуінің шешімі. Бордың сәйкестік принципі.
24. Серпінді толқын энергиясы. Энергия ағынының тығыздығы.. Умов векторы
25. Толқындардың суперпозиция принціпі. Топтық жылдамдық пен фазалық жылдамдық және олардың арасындағы байланыс. Толқындардың интерференциясы.
26.Сутегі атомы үшін Шредингер теңдеуі. Энергетикалық деңгейлер. Деңгей ені. Спин.Кеңістіктің квантталуы. Паули принципі.
27. Кванттық механикадағы микробөлшектердің күйі. Толқындық функция және оның статистикалық мағынасы. Шредингердің уақыттық және стационар теңдеуі
28. Электромагниттік өріс үшін толқын теңдеу. Толқындық теңдеу. Электромагнитті толқын қасиеттері.
29.Жарық толқыны және оның сипаттамалары. Жарықтың монохраматтылығы және когеренттілігі. Жарық жылдамдығын анықтау тәжерибелері.
30. Заттардың корпускулалық-толқындық дуализмді. Де Бройль гипотезасы және оны тәжерибелермен растау. Де Бройль толқынының қасиеттері.
31.Жарық интерференциясы және оны бақылау тәсілдері.
32. Комптон эффектісі және оның элементар теориясы.
33. Жарыққ дифракциясы. Гюгенс-Френель принціпі. Френельдің зоналар әдісі.
34. Құйынды электр өрісі. Ығысу тогы. Толық ток тығыздығы.
35.Бір саңылаудағы дифракция. Дифракциялық тор. Кеңістіктік тор. Голография.
36.Электромагниттік энергия ағынының тығыздығы. Пойнтинг векторы. Дипольдің сәуле шығаруы.
37. Жарық поляризациясы. Екі диэлектрик ортаның шекарасындағы жарықтын шағылу мен сыну кезіндегі поляризация.
38. Фотондар. Жарық кванттарының энергиясы және импульсы. Жарық қысымы.
39. Жылулық сәуле шығару. Жылулық сәуле шығару заңдары. Абсалют қара дененің сәуле шығару проблемалары. Планк формуласы және кванттық гипотезасы .
40. Ядроның байланыс Энергиясы. Массалық ақау.
41. Жылулық сәуле шығару. Стефан –Больцман және Вин заңдары..
42. Электромагниттік толқын энергиясы. Энергия ағынының тығыздығы. Пойнтинг векторы. . Электромагниттік толқын импульсі.
43.Заттардың корпускулалық-толқындық дуализмді. Гейзенбергтің анықталмағандық қатынастары.
44. Гармоникалық осциллятор. Серіппелі маятник.
45. Механикалық тербеліс энергиялары. Кинетикалық потенциялдық және толық энергия.
46. Радиоактивті сәуле шығару және оның түрлері.
47. 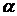 -ыдырау және
-ыдырау және  -ыдырау. олардың заңдылықтары мен қасиеттері.
-ыдырау. олардың заңдылықтары мен қасиеттері.
48 Еріксіз тербелістердің дифференциалды теңдеуі және оның шешімі.
49  -сәуле шығару және оның заңдылықтары мен қасиеттері.
-сәуле шығару және оның заңдылықтары мен қасиеттері.
50 Электромагнитті сәуле шығарудың корпускулалы-толқындық дуализмі. Фотоэффект. Фотоэффектінің негізгі заңдары. Фотоэффект үшін Эйнштейн теңдеуі.
51 Жарық поляризациясы. Екі диэлектрик орта шекарасындағы жарықтың
шағылу, сыну кезіндегі поляризация.
52. Құйынды электр өрісі. Ығысу тогы. Максвелл теңдеулер жүйесі. Электр және магнит өрістерінің салыстырмалылығы
Дата добавления: 2018-02-15; просмотров: 3239; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



