Дисперсия света: нормальная и аномальная.
Дисперсия света – это зависимость показателя преломления вещества от частоты световой волны . Эта зависимость не линейная и не монотонная. Области значения ν, в которых
 (или  )
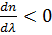| (10.2.1) |
соответствуют нормальной дисперсии света(с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров.
Дисперсия называется аномальной, если
| (или  ),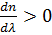
| (10.2.2) |
т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.
Зависимости n от ν и λ показаны на рис. 10.4 и 10.5.
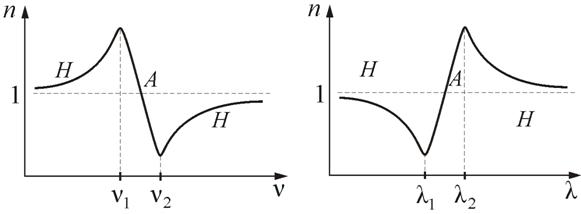
| Рис. 10.4. | Рис. 10.5 |
В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости υ (в недиспергирующей среде u=V).
Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением: 
, где ω=2πv, 
. Тогда
. Отсюда можно записать:
 .
| (10.2.3) |
Таким образом, при нормальной дисперсии u < υ и .
|
|
|
При аномальной дисперсии u > υ, и, в частности, если 
, то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.
34. Теория дисперсии
Дисперсиейсвета называется зависимость фазовой скорости света в среде от его частоты v.
Так как v=с/n, то дисперсией света можно назвать также зависимость показателя преломления n среды от частоты v световой волны.
Наиболее отчетливо дисперсия света проявляется при прохождении белого света через призму. За призмой лучи белого света окажутся разложенными на составляющие цвета - в спектр. Полученный спектр называют призматическим, в отличии от дифракционного спектра, даваемого дифракционной решеткой.
|
|
|
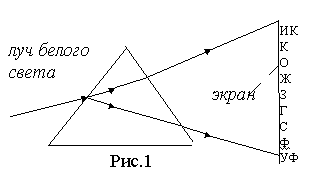Согласно электронной теории дисперсии луч белого света "раскачивает" электроны в атомах, причем сильнее всего "раскачивает" в том случае, когда частота световой волны близка к собственной частоте колебаний электрона в среде v0, т.е.в случае резонанса.
Степень взаимодействия света с веществом, а, следовательно, и скорость распространения света зависит от близости к резонансу, т.е. от v - v0, а также от параметра b - характеризующего затухание свободных колебаний электрона.
Согласно электронной теории дисперсии справедлива следующая приближенная формула для показателя преломления
,(3)
где A=2pNe2/m, где N - концентрация атомов, e, m заряд и масса электрона.
На рис. 2 приведен график зависимости n от v при b =0 (штриховая линия) и с учетом b (сплошная линия). Области А и С для которых с увеличением частоты v показатель преломления возрастает, называются областями нормальной дисперсии, т.е. для них
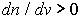или 
(4)0
Область В, для которой с увеличением частоты v показатель преломления уменьшается называется областью аномальной дисперсии, т.е. для нее
или 
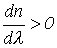(5)
В области аномальной дисперсии поглощение света очень велико.
Групповая скорость
|
|
|
В результате суперпозиции нескольких синусоидальных волн образуется несинусоидальная волна с каким-то набором частот и волновых чисел. За скорость распространения такой волны в пространстве берётся скорость распространения фиксированной амплитуды. Но если в случае простой синусоидальной волны эта скорость совпадает со скоростью распространения фиксированной фазы (мы назвали эту скорость фазовой), то в случае сложной несинусоидальной волны сама амплитуда зависит от времени и координат (см. предыдущий пример). Амплитуда сложной волны есть:
Фиксированная амплитуда А будет удовлетворять условию: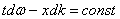 
Взяв полный дифференциал от этого выражения, получим (независимые координаты у нас x и t): 
Скорость распространения фиксированной амплитуды в несинусоидальной волне получается следующей:
Эта скорость называется ГРУППОВОЙ СКОРОСТЬЮ волны. Она в общем случае отличается от фазовой скорости n:
Связь между этими скоростями можно легко получить (учтя зависимость частоты и волнового числа от длины волны):
Среда называется ДИСПЕРГИРУЮЩЕЙ, если в ней волны разной длины распространяются с разной скоростью. Зависимость скорости волны (фазовой) от длины волны (или, что то же самое, от частоты) называется ДИСПЕРСИЕЙ.
|
|
|
Видно, что групповая скорость будет совпадать с фазовой только в недиспергирующих средах, где составляющие сложной волны будут перемещаться с одинаковой скоростью, и сама сложная волна не будет менять своей формы (не будет "расплываться").
Для МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ (так называется простая синусоидальная волна, имеющая одну частоту) фазовая и групповая скорости всегда совпадают, даже в диспергирующих средах.
Фазовая скорость есть чисто абстрактное математическое понятие, эта скорость не связана с перемещением в пространстве чего-либо материального.
Групповая скорость связана с перемещением в пространстве возмущения фиксированной амплитуды; поскольку энергия волны связана с её амплитудой, групповая скорость есть скорость распространения энергии в пространстве.
В общем случае фазовая скорость может превышать скорость света (в случае, например, электромагнитной волны, или волн Де Бройля). Групповая же скорость, в полном согласии с теорией относительности, всегда меньше либо равна скорости света.
Дата добавления: 2018-02-15; просмотров: 5564; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!