Теория прочности (энергетическая теория прочности)
Было предложено в качестве критерия пластичности принять энергию, связанную с изменение формы элемента.
Для простого растяжения в продольном состоянии σ1 = σкр , σ2 = σ3 = 0, 
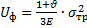
Считая эти 2 состояния равновесными и приравнивая энергии формоизменения получил выражение для эквивалентного напряжения.
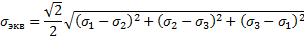
Условие прочности по 4 теории прочности: 
Для плоского напряжённого состояния (σ1 = 0) условие прочности по 4 теории прочности:
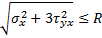
3 и 4 теории прочности хорошо согласуются с экспериментом и широко используются в практических расчётах для материалов, одинаково сопротивляющихся растяжению и сжатию.
Теория Мора
Предельное состояние наступает тогда, когда на некоторой площадке с нормалью n величина τ достигает опасного значения, зависящего от действующей на этой площадке σ.
Условие прочности по теории Мора: 
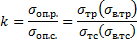
Недостаток: здесь, как и в 3 теории прочности, не учитывается влияние σ2, при k=1 критерий по Мору совпадает с критерием теории τmax. Теория Мора применяется для материалов, по-разному сопротивляющихся растяжению и сжатию.
(для большего понимания теории Мора лучше почитать учебник, т.к. тупо переписывать его сюда смысла нет)
Определение перемещений при изгибе. Дифференциальное уравнение изогнутой оси балки. Метод непосредственного интегрирования.
При прямом поперечном изгибе все внешние силы изгибающие балку располагаются в одной из главных плоскостей инерции тела (yox, zox) и направлены ^ продольной оси стержня (ось х). При такой деформации продольная ось балки искривляется, образуя плоскую кривую, плоскость которой совпадает с той же главной плоскостью инерции балки (yox, zox). Эта искривленная ось носит название изогнутой оси балки, или упругой линии балки. При прямом изгибе в какой области действуют внешние силы, в той же плоскости прогибается балка.
Введем систему координат: х -продольная ось, у,z- поперечная, ось у направлена вверх. Начало координат крайняя левая точка.
|
|
|
V- вертикальное перемещение (прогиб). U- горизонтальное перемещение. q-угол поворота поперечного сечения балки.
Т.к. вертикальное перемещение балки V<<U, то в расчетах горизонтальными перемещениями пренебрегают. И когда говорят, что необходимо найти перемещение при прямом изгибе это значит необходимо определить прогиб v и угол поворота q поперечного сечения балки.
Для выбранной системы координат введем следующее правило знаков:
Прогиб V считается +, если он совпадает с положительным направлением оси y (направлен вверх). Угол поворота поперечного сечения q считается +, если поперечное сечение балки поворачивается против часовой стрелки.
|
|
|
Искомые перемещения V и q связанны соотношением: q»tgq= 
Таким образом, уравнение углов поворота q(х) можно получить, если взять дифференциал от уравнения изогнутой оси балки V(x).
Дата добавления: 2018-02-15; просмотров: 990; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!