Полная проверка прочности при плоском изгибе. Потенциальная энергия деформации балки при плоском изгибе. Особенности расчета составных балок.

Полная проверка прочности при плоском изгибе

1. строятся эпюры Q(y), M(z)

2. определяется опасное сечение балки:

а) сечение, где M(z) принимает max значение по модулю;

б) сечение, где Q(y) принимает max значение по модулю;

в) сечение, где Q(y) и M(z) достигает по модулю достаточно больших величин;

3. для каждого опасного сечения строятся эпюры σ(x) и τ(yx). Для каждого опасного сечения определяются опасные точки и делается проверка прочности.

а) точки, где σ(x) max – это точки, лежащие на наружных поверхностях балки. Имеет место линейное напряженное состояние (осевое растяжение/сжатие)

σ(x) = σ(max/min)

τ(yx) = τ(xy)=0

Условие прочности имеет вид:

R(y) – расчётное сопротивление по пределу текучести

[σ] – допускаемое напряжение

б) точки, где τ(yx) достигает max - точки, лежащие на нейтральной оси балки – чистый сдвиг

σ(x) = 0

τ(yx) = τ(max/min)

τ(max) =

R(s) – расчётное сопротивление при сдвиге

[τ] – допускаемое касательное напряжение

в) точки, в которых σ(x) и τ(yx) достигают достаточно больших значений, имеет место плоское напряжённое состояние. Делается проверка прочности по 3 теории прочности:

σ(1) – σ(3) ≤ R(y)            – условие прочности

Потенциальная энергия деформации при плоском изгибе

Чистый изгиб. В поперечных сечениях балки возникает только M(изг)

ρ – радиус кривизны

Примем условно левое поперечное сечение балки за неподвижное, тогда правое повернётся на угол dϴ по отношению к левому, ρ н.с. связвн с M(z).

Т.к. волокна на уровне с н.с. не меняют своей длины, то dx = ρdϴ и из этого следует, что . Зависимость между М и dϴ при упругой работе материала линейна, поэтому работа М при повороте сечения на угол dϴ будет равна S_∆OAB

СледовательноE(п) участка балки длиной dx равна

Полная Е(п) определяется интегралом по длине балки  – эту формулу используют для определения потенциальной энергии балки и при наличии Q (при ПППИ), вклад которой в общую энергию невелик. эта потенциальная энергия может быть определена по формуле , где k – коэффициент, зависящий от форм поперечного сечения балки и учитывает неравномерность распределения τ по высоте сечения, G – модуль сдвига, A – площадь поперечного сечения.(Обычно U_Q пренебрегают)

Особенности расчёта составных балок

Виды составных балок:

(а) клеевые

 (б) сварные

(в) клепаные

Составные балки используются в том случае, когда требуемые по условию прочности размеры поперечного сечения не обеспечивается одним стандартным элементом. Соединительные элементы составных балок (клей, швы, заклёпки) должны обеспечивать работу всего соединения, как единого целого.

1. Клеевое соединение

Разделим балку по шву, рассмотрим нижнюю часть. В продольных сечениях монолитной балки возникают касательные напряжения τ(yx), которые определяются по формуле Журавского  (воспринимает клеевой слой)

условие прочности для продольного клеевого шва балки

R_ср – расчётное сопротивление на срез клеевого шва

 

 

Особенности расчёта объединения 2х одинаковых балок с прямоугольной площадью сечения размерами b и h и одной монолитной балки. Если положить одну балку на другую, не склеивая их, то каждая балка будет работать отдельно, воспринимая ½ общей нагрузки. Н.о. этих балок будут проходить через центр тяжести отдельного сечения. По плоскости контакта будет скольжение.

При изгибающем моменте нижние волокна верхней балки будут длиннее сжатых верхних волокон нижней балки. σ₀ в крайних волокнах каждой балки равны.

 , где М – сумма моментов, воспринимаемая 2мя балками сечение hb каждая.

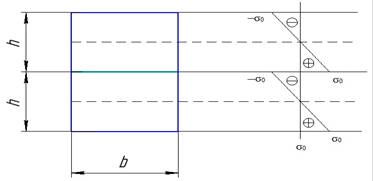
Если склеить обе балки – сделать монолитной, то н.о. будет проходить через центр тяжести объединенного сеченияи напряжение в крайних волокнах будут равны

Таким образом, объединение 2х балок в одну монолитную позволяет увеличить грузоподъёмность балки в 2 раза.

2.Сварное соединение

При расчёте сварных швов определяем полную сдвигающую силу Т, которая возникла бы в продольном сечении на сдвиге соединения стенки с палкой, если бы балка была сплошной.

(1)

Стенка с полкой соединяется через сварные швы высотой h, τ среза в плоскостях А-А сварного шва равны.

(2)

Решая совместно (1) и (2), получим условие прочности сварного шва по срезу

3. Заклёпочные соединения

Клёпанные балки вертикальные и горизонтальные заклёпки одинакового диаметра расположены по длине балки на одинаковом расстоянии a(шаг заклёпки).

Горизонтальные двухсрезные заклёпки оказываются в более тяжёлых условиях, т.к. отсекаемая для них часть сечения состоит из полки и 2х уголков

, сила, приходящаяся на 2 заклёпку T*a

Условие прочности для заклёпки по срезу: (3)

R_ср – расчётное сопротивление на срез заклёпки

Т – сдвигающая сила

Условие прочности для заклёпки по смятию: (4)

, где d – диаметр заклёпки,  - min толщина листов, направленных в одну сторону действия нагрузки. Обычно d заклёпки задаётся по конструктивным соображениям, а из (3) и (4) определяется и выбирается min значение.

Проводится проверка основного металла с учётом ослаблений, вызванных отверстиями под заклёпки.Для этого из общего момента инерции всего сечения вычитается момент инерции ослаблений относительно н.о.

Горизонтальные и вертикальные заклёпки показаны в одном сечении, хотя в действительности в ослабленное поперечное сечение попадают либо вертикальные, либо горизонтальные заклёпки. Учет ослаблений от вертикальных и горизонтальных заклёпок в одном сечении завышает значение I_осл, что идёт в запас прочности.

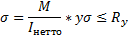
τ вычисляется без учёта ослаблений.

 

29. Теории прочности. Теории предельных состояний. Теории Мора.
Основные понятия
При небольших нагрузках большинство материалов деформируется упруго (находятся в упругом состоянии), с ростом нагрузок появляются пластические деформации: материал переходит в пластичное состояние. Условия, при которых материал переходит из упругого в пластичное состояние – критерии пластичности.

С дальнейшим ростом нагрузок происходит образование трещин и наступает состояние разрушения. Условия, при которых происходит разрушение – критерии прочности. Хрупкие материалы разрушаются, минуя стадию пластичности.

Критерии пластичности и прочности – критерии предельных состояний.

Деление материалов на пластичные и хрупкие проводят по результатам их механического поведения при растяжении/сжатии образцов в условиях линейного напряжённого состояния.

При растяжении пластичные деформации появляются, когда σ в поперечных сечениях образца достигают значения предела упругости, который близок к величине предела текучести материала, поэтому за критерий пластичности при линейном напряжённом состоянии (растяжение) можно взять предел текучести материала при растяжении σ_тр.

Можно установить величину σ, когда возникают пластичные деформации при сжатии. Предел пластичности – σ_тс (предел текучести при сжатии)

При испытаниях на чистый сдвиг определяется τ_т, при котором появляются пластические деформации.

В обще случае в опасной точке конструкции реализуется объёмное напряжённое состояние, которое характеризуется 3мя главными напряжениями σ₁ σ₂ σ_3. При некотором пространственном напряжённом состоянии с главными напряжениями σ₁ σ₂ σ₃ будем эти напряжения увеличивать, не меняя ориентации главных площадок – простое нагружение до тех пор, пока не наступит предельное состояние: пластичные деформации, или начнётся разрушение.

Число, которое показывает во сколько раз необходимо увеличить σ₁ σ₂ σ₃ до наступления предельного состояния – коэффициент запаса.

Если в 2х напряжённых состояниях коэффициенты запаса равны, то такие напряжённые состояния – равноопасные.

Эталонным напряжённым состоянием выбирают состояние при растяжении, характеризуемое одним напряжением, которое называется эквивалентным (приведённым).

Эквивалентное напряжение – напряжение, которое следует создать в растянутом образце, чтобы его состояние было равноопасно заданному напряжённому состоянию.

В

А

Расчёт на прочность в опасном напряжённом состоянии А заменяют расчётом на осевое растяжение В, где коэффициент запаса определяется соотношением

σ_оп.р. – опасное значение напряжения при растяжении.

Т.к. приняли допущение о том, что критерии предельного состояния может быть записан в виде числа – коэффициент запаса n. Необходимо выразить σ_экв через главные напряжения, что и устанавливает теории предельных состояний (теории прочности)

Теории прочности
1 теория прочности

Предельное состояние наступает тогда, когда наибольшее по абсолютной величине главное напряжение достигает предельного значения = опасному значению при растяжении или сжатии (σ_оп.р. или σ_оп.с. соответственно).

Если σ₁>=σ₂>=σ₃>=0, то условия наступления предельного состояния:

(5)

Если 0 >=σ1>=σ2>=σ3, то:

σ_экв= |σ₃^оп| = σ_оп.с.(6)

Если σ₁>0, σ₃<0, то записывают (5) и (6).

по первой теории прочности σ_экв = σ_гл.^max/min в точке

условие прочности по 1 теории прочности:

σ₁ <= R_p или [σ_p] , если σ₁>=σ₂>=σ₃>=0

| σ₃| <= R_c или [σ_с] , если 0 >=σ1>=σ2>=σ3

R_p, R_c, [σ_с], [σ_p] – расчётные сопротивления, допускаемые значения при растяжении/сжатии

Недостатки: только одно главное напряжение (σ₁ или σ₃) влияет на величину σ_экв, влияние 2х других напряжений на наступление предельных состояний не учитывается, хотя в общем случае оно существенно.

2 теория прочности (теория max главных деформаций)

Предельное состояние наступает, когда max главная деформация достигает опасного предельного значения, которое определяется из опыта на растяжение. Условие наступления предельного состояния: 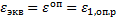(7)

Опасное состояние наступает тогда, когда σ равно σ_т.р. (предел текучести при растяжении), которое близко по значению пределу пропорциональности σ_пц (при наличии пластических деформаций) или пределу прочности σ_в.р. (при хрупком разрушении). В обоих случаях  можно определить из закона Гука:

При объёмном напряжённом состоянии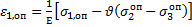

Соотношение (7) можно записать виде:

Эквивалентные напряжения по 2 теории прочности:

Условие прочности по 2 теории прочности: : , где σ₁ σ₂ σ₃ – главные напряжения.

Во 2й теории прочности учитывается влияние всех 3х главных напряжений, и оно лучше соответствует экспериментальным данным, особенно когда в условиях сложного напряженного состояния в предельном состоянии является хрупкое разрушение путём отрыва. Опытные данные по наступлению предельного состояния пластичности не соответствует этой теории, что резко ограничивает область применения.

3 теория прочности (теория max τ)

При растяжении образца было установлено, что пластичные деформации появляются в виде следов плоскостей скольжения (линии Модерса-Чернова), располагаясь под углом 45º к направлению растяжения образца. На этих площадках действуют τ_max, которые в момент появления пластических деформаций равны τ_max= τ^оп = 1/2σ_тр.

Т.к. , то критерий пластичности по 3 теории прочности:

и из этого следует, что

Условие прочности по 3 теории прочности:

Для плоского напряжённого состояния:

Экспериментальная проверка показала, что 3 теория прочности удовлетворительно описывает наступление состояния пластичности для большинства материалов (хрупких и пластичных)

Недостатки: она не учитывает главное напряжение σ₂

---

Дата добавления: 2018-02-15; просмотров: 842; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!