Моменты инерций прокатных сечений (двутавров, швеллеров, уголков и т.д.) приводятся в таблице сортамента.
Зависимость между моментами инерции относительно повернутых осей.
Рассмотрим произвольное сечение (рис. 5.12) и связанную с ним систему координат YOZ. Повернем оси координат на угол α > 0, образовав новую систему координат Z1OY1.
Выразим координаты точки Вв новой системе координат (z1, y1) через координаты той же точки в старой системе (z, y). Для этого найдем проекции ломаной ВСО на оси z1и y1: 
Осевой момент инерции относительно z1и y1
Свойства моментов инерции:
Если при неизвестной фигуре исходную систему координат ZOY повернуть на угол α и образовать новую систему координат Z1OY1 , то 
При повороте координатных осей сумма осевых моментов инерций фигур остается постоянной.
Понятие о главных осях и главных моментах инерции
Оси, относительно которых центробежный момент равен 0 (Jzy=0), а осевые моменты инерции принимают экстремальные значения (Jmax, Jmin),называются главными осями(U, V)
Главные оси, проходящие через центр тяжести всего сечения, называются главными центральными осями.
Осевые моменты относительно главных осей называются главными моментами инерции (Jmax, Jmin)
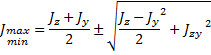
Любая ось симметрии ( 
является главной осью.
Свойства главных моментов инерции:
1. 
2. Для сечений, не имеющих осей симметрии положение главных осей определяется по формуле
-угол, показывающий направление главных осей
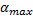-угол между z и осью, относительно которой момент инерции принимает max значение
|
|
|
-угол между z и осью, относительно которой момент инерции принимает min значение
Правило знаков: положительное направление углов откладывается от оси z против часовой стрелки
20. Кручение валов. Внутреннее усилие при кручении и их правило знаков. Построение эпюр крутящих моментов. Проверка эпюр. Напряжение и деформация при кручении.
Кручение-деформация прямого стержня, при действии нагрузок в виде пар сил в плоскости, перпендикулярной продольной оси стержня. В случае кручения прямого стержня силы внутреннего взаимодействия суммируются к одному внутреннему силовому фактору.
Внутреннее усилие – крутящий момент Мкр= Мх
Правило знаков – крутящий момент положителен, если при взгляде со стороны отброшенной части пара сил, ему соответствующая, вращает выделенную часть по часовой стрелке.
Мысленно разрежем сечением стержень на две части и рассмотрим равновесие каждой из них под действием приложенных к ним внешних моментов и положительного крутящего момента
а) ∑mx=0
m1-m2+ Мхlll=0
Мхlll= -m1+m2=2.33 кН*м
б) ∑mx=0
-m3-m4+ Мхlll=0
Мхlll= m3+m4=2.33 кН*м
А и Б дают одинаковые условия крутящего момента. Условие равновесия всего стержня имеет вид
Крутящий момент в произвольном сечении стержня = алгебраической сумме моментов всех внешних сил, взятых по одну сторону от сечения Мх= Мкр=∑mx
Проверка эпюры внутренних усилий: в сечении стержня, где приложен внешний момент, будет скачок, равный величине внешнего момента.
|
|
|
Напряжение и деформация при кручении:
1. Все поперечные сечения круглого стержня при кручении остаются плоскими и только поворачиваются вокруг продольной оси
2. Радиус поперечных сечений не искривляется
3. Расстояния между поперечными сечениями не изменяются
При кручении круглого стержня в его поперечных сечениях отсутствуют нормальные напряжения, а возникают только касательные напряжения:
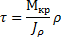
– полярный момент инерции
-расстояние от точки до центра тяжести поперечного сечения
Наибольшие касательные напряжения будут в точках на контуре поперечного сечения ( 
R)
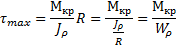
- полярный момент сопротивления
21. Условие прочности и жесткости при кручении. Подбор сечений по условиям прочности и жесткости. Напряженное состояние. Потенц. энергия упругих деформаций при кручении.
Условие прочности:
Rs-расчетное сопротивление материала при сдвиге, [τ] – допускаемое касательное напряжение
З типа расчета:
1. Проверочный (поверочный)
|
|
|
2. Проектировочный
3. Расчет грузоподъемности
Для определения угла закручивания (деформаций при кручении) используется:
Если по длине участка крутящий момент постоянный, то 
Мкр- крутящий момент, L – длина участка, G – модуль сдвига, Jρ-полярный момент инерции, G* Jρ-крутильная жесткость
Условие жесткости:
[ϕ] [θ]- допускаемые значение угла закручивания и относительного угла закручивания
З типа расчета:
1. Проверочный (поверочный)
2. Проектировочный
3. Расчет грузоподъемности
Проектировочный расчет (подбор сечения) ведется по условиям:
По условию прочности 
По условию жесткости 
Напряженное состояние
Рассмотрим продольное сечение, пересекающее стержень по любому его диаметру. На основании закона парности касательных напряжений можно заключить, что касательное напряжение в любой точке этого продольного сечения равно по модулю напряжению в той же точке, но в плоскости этого сечения. 
При кручении напряженное состояние – чистый сдвиг, при котором главные площадки наклонены под углом 450 к площадкам чистого сдвига, т. к. во всех точках поверхности стержня ориентация главных площадок будет аналогичной, то траектории главных напряжений при кручении круглого стержня представляют собой 2 взаимно ортогональных друг другу семейства винтовых линий, каждая из которых пересекает образующую цилиндра под углом 450.
|
|
|
Дата добавления: 2018-02-15; просмотров: 1023; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!