Практические расчеты на сдвиг. Расчет заклепочных (болтовых) и сварных соединений.
Соединения бывают: заклепочные (болтовые), сварные, склеивание.
Заклепочные (болтовые). Расчет заклепочного соединения имеет целью определить необходимое количество заклепок и проверить прочность соединяемых элементов в пределах стыка.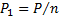 
, где n – число заклёпок. Под действием силы P1, в стержне заклепки возникают касательные усилия: 
, где d- диаметр заклепки.
Условие обеспечивающее прочность по срезу заклепки: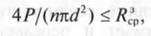 
Формула для проверки прочности основного элемента 
Условие прочности по смятию: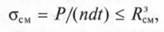 
4.3. соединение листов внахлестку;
4.4 соединение встык;
а. работа заклепки под действием силы Р1; б. сечение заклепки диаметральной плоскостью ;
Сварные.Расчетом сварных соединений сводится к расчету прочности швов, основным видом деформации которых является сдвиг.Если два соединяемых листа стремятся сдвинуться, то во всех продольных швах возникают касательные напряжения, выражающие влияние одной части шва на другую.
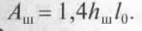hш- высота шва , Rсв- расчетное сопротивление срезу материала сварного шва.
17. Геометрические характеристики плоских фигур. Площадь поперечного сечения, статические моменты площади, моменты инерции, моменты сопротивления и радиусы инерции. Моменты инерции простых фигур.
Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения.
Площадь поперечного сечения является геометрической характеристикой, которая определяет напряжения при растяжении (сжатии). Размерность м2
|
|
|
Статический момент (момент первого порядка)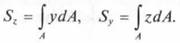 
, где А – площади простых фигур; у,z – координаты центра тяжести этих фигур;
Центральными называются оси, проходящие через центр тяжести фигуры. Статические моменты относительно этих фигур равны 0.
Главные центральные оси – это оси, осевые моменты инерции относительно которых принимают свои экстремальные значения (максимум и минимум).
Осевой (центробежный) момент инерции сечения относительно осей у, zразмерность м4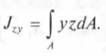 
Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки. 
Радиус инерции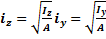 
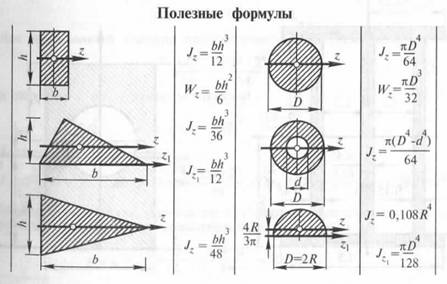
Моменты инерции простых фигур.
Прямоугольник: 
Треугольник: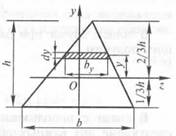 
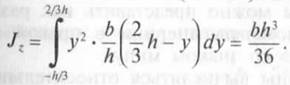z– центральная ось параллельна основанию треугольника
Круг: 
; 
;
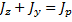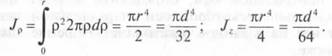
Двутавр: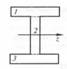 
ПНС-предельное напряжсост
Понятие моментов инерции сечений. Зависимость между моментами инерции относительно параллельных осей. Моменты инерции составных фигур.
Статический момент (момент первого порядка) 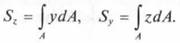, где А – площади простых фигур; у,z – координаты центра тяжести этих фигур;
|
|
|
Осевой (центробежный) момент инерции сечения относительно осей у, z размерность м4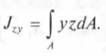
Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки.
Зависимость между моментами инерции относительно параллельных осей: Осевой момент инерции сечения относительно любой оси равен моменту инерции относительно центральной оси параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.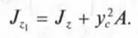 
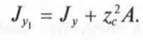
Момент инерции сложной фигуры равен сумме моментов инерции ее составных частей
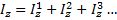Координату центра тяжести определяем по формуле 
А1 – площадь первой фигуры, А2 – площадь второй фигуры, у1 – расстояние от оси z до центра тяжести фигуры 1, у2 – расстояние от оси z до центра тяжести фигуры 2.
Дата добавления: 2018-02-15; просмотров: 2538; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!