Определение опорных реакций статически определимой балки. Построение эпюр

Для статически определимой стальной балки требуется:

1) Построить эпюры поперечных сил Q и момент изгибающих М, эпюру прогибов;

2) Подобрать стальную балку двутаврового сечения, если . Проверить прочность выбранной балки по касательным напряжениям при . Определить значение нормального и касательного напряжения в т. К, расположенной на расстоянии от 0-ой линии сечения а-а двутавровой балки;

3) Построить эпюры нормальных и касательных напряжений для сечения а-а.

Дано:

Рисунок 11 – Расчетная схема

Определяем опорную реакцию из условия равновесия. Запишем сумму моментов относительно точки А:

......................................................................................... (128)

;(129)

.(130)

Отсюда получим значение реакции опорR_B:

кН. (131)

Определяем опорную реакцию из условия равновесия. Запишем сумму моментов относительно точки В:

......................................................................................... (132)

;(133)

.(134)

Отсюда получим значение реакции опорR_А:

кН. (135)

Для проверки полученных значений запишем сумму всех сил на ось Y:

;(136)

. (137)

0=0, реакции определены верно.

2) Определяем Q и M на каждом участке. Для этого применим метод сечений.

Сечение 1 (Рисунок 12):

Рисунок 12 – Сечение 1

0 ≤ х₁ ≤ 4 м

; (138)

; (139)

; (140)

. (141)

Сечение 2 (Рисунок 13)

Рисунок 13 – Сечение 2

0 ≤ х₂ ≤ 4 м

; (142)

; (143)

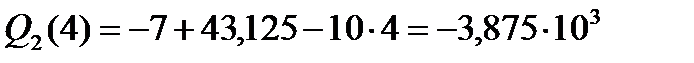. (144)

Определим точку, в которой Q₂ = 0. Приравняем уравнение (142) к нулю. Получим:

; (145)

. (146)

Для нахождения момента запишем сумму моментов относительно центра тяжести сечения 2:

;(147)

;(148)

;(149)

.(150)

Сечение 3 (Рисунок 14):

Рисунок 14 – Сечение 3

0 ≤ х₃ ≤ 2 м

; (151)

Для нахождения момента запишем сумму моментов относительно центра тяжести участка 3:

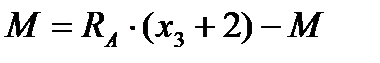; (152)

; (153)

.(154)

Сечение 4 (Рисунок 15)

Рисунок 15 – Сечение 4

0 ≤ х₄ ≤ 2 м

; (155)

Для нахождения момента запишем сумму моментов относительно центра тяжести сечения4:

;(156)

;(157)

.(158)

По найденным значениям построим эпюры Q и M (Рисунок 21).

3) Находим опасное сечение. Опасное сечение возникает там, где максимален изгибающий момент:

;(159)

. (160)

Подберём прямоугольное сечение для балки.

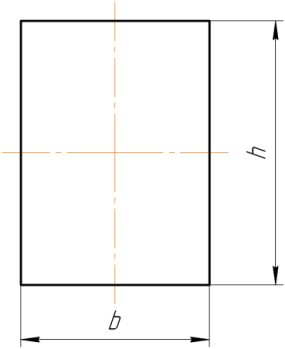
Рисунок 16– Прямоугольное сечение

. (161)

Для прямоугольного сечения h=2b, тогда:

; (162)

W_тр = W_y, тогда:

; (163)

. (164)

Найдём требуемую высоту сечения h:

. (165)

Найдём площадь прямоугольного поперечного сечения:

. (166)

Подберём квадратное сечение для балки.

Рисунок 17 – Квадратное сечение

; (167)

; (168)

; (169)

; (170)

. (171)

Подберём круглое сечение для балки.

Рисунок 18 – Круглое сечение

; (172)

м; (173)

м². (174)

Подберём кольцевое сечение для балки:

Рисунок 19 – Кольцевое сечение

см³; (175)

см; (176)

; (177)

см². (178)

Подберём двутавровое сечение для балки:

Согласно ГОСТ 8239-89 выбираем двутавр № 24. Для которого W_y=289 см³, t=0,95 см, b=11,5 см, Q_max=27,3 кН, Y_y=3460 см⁴, d=0,56 см, S_y=S_max=163, h=24 см.

Рисунок 20 – Двутавровое сечение

Площадь сечения A_дв= 34,8

Выбираем наиболее рациональную форму сечения по расходу материала. Для этого сравниваем площади всех подобранных сечений:

; (179)

; (180)

; (181)

. (182)

Наиболее рациональной формой сечения балки (балкой с наименьшим весом) является двутавровое сечение, наименее – круглое поперечное сечение. У двутаврового сечения большая часть площади поперечного сечения расположена как можно дальше от нейтральной оси, у круглого сечения большая часть расположена на нейтральной оси.

4) Проверим прочность выбранной балки по касательным напряжениям при :

; (183)

22,9 МПа<100 МПа. (184)

Прочность обеспечена.

5) Определим значение нормального напряжения в точке К, расположенной на расстоянии z= = от нейтральной оси у в сечении а-а.

Учитывая, что изгибающий момент М_а-а вызывает сжатие верхних волокон балки, для точки К получаем:

(185)

6) Определим значение касательного напряжения в т.К сечения а-а. Поперечная сила в сечении Q=28 кН.

Для определения касательного напряжения в т.К проведем через эту точку прямую в-в, параллельную нейтральной оси У. Затем определим статический момент S части сечения, отсеченной прямой в-в, относительно У.

За отсеченную можно принимать как часть сечения, расположенную выше прямой в-в, так и часть, расположенную ниже этой прямой.

Для верхней части:

см³; (186)

МПа. (187)

7) Построим эпюру нормальных напряжений в сечении а-а. Нормальные напряжения по высоте сечения изменяются по линейному закону.

В точках нейтральной оси У нормальные напряжения возникают в крайних точках поперечного сечения, причем в верхних точках сжимающие, а в нижних растягивающие.

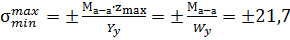МПа. (188)

Эпюра показана на рисунке

8) Построим эпюру касательных напряжений в сечении а-а двутавровой балки.

Для этого определим касательные напряжения в некоторых характерных точках поперечного сечения балки.

В верхней точке 1 касательные напряжения =0, так как вся площадь поперечного сечения расположена ниже этой точки, а поэтому статический момент S относительно оси у равен нулю.

В точке 2, расположенной непосредственно над линией, проходящей через нижнюю грань верхней полки двутавра:

МПа. (189)

Между точками 1 и 2 направления изменяются по квадратной параболе. В стенке двутавра в точке 3, расположенной непосредственно под точкой 2, касательные напряжения:

МПа. (190)

Так как ширина в полке двутавра значительно больше толщины d вертикальной стенки, то эпюра касательных напряжений имеет резкий скачок в уровне, соответствующем нижней грани верхней полки. Ниже точки 3 в стенке двутавра изменяются по закону квадратной параболы. Наибольшие касательные напряжения возникают на уровне нейтральной оси:

МПа. (191)