Оценка устойчивости по критерию Гурвица
По определению критерия Гурвица: система устойчива, если определитель характеристического уравнения передаточной функции, составленный по закону Гурвица положителен, и положительны все его диагональные миноры.
Для нахождения характеристического уравнения найдем передаточную функцию всей системы. Для этого сначала найдем передаточную функцию системы в разомкнутом состоянии. Так как элементы разомкнутой системы соединены последовательно, то WРАЗ(s) равна произведению передаточных функций элементов:
;
;
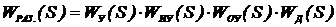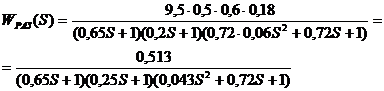
передаточная функция системы в замкнутом состоянии:
;
Характеристическое уравнение передаточной функции:
По правилу Гурвица составляем определитель:
минор 3-го порядка:
>0
минор 2-го порядка:
> 0
минор 1-го порядка:
> 0
Вывод: система устойчива по критерию Гурвица, так как коэффициенты характеристического уравнения одного знака, определитель Гурвица и все его диагональные миноры положительны.
Оценка устойчивости по критерию Михайлова
По определению критерия Михайлова: для устойчивости системы необходимо и достаточно, чтобы при изменении угловой частоты w от нуля до бесконечности, годограф, описываемый концом вектора 
начинался на вещественной положительной полуоси, и, вращаясь только против часовой стрелки, нигде не обращаясь в ноль, проходил, повернувшись на угол pn/2, последовательно число квадрантов, равное степени n характеристического уравнения. Если хотя бы одно из этих условий не выполняется, то система не устойчива.
|
|
|
В характеристическом уравнении сделаем замену: S ® jw, тогда полином в знаменателе будет выглядеть следующим образом:
Выделим вещественную и мнимую части:
 |
Действительная часть:
Дата добавления: 2018-02-15; просмотров: 393; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!