Методические указания по выполнению. домашнего задания (контрольной работы)
домашнего задания (контрольной работы)
При самостоятельном изучении курса следует руководствоваться рабочей программой по дисциплине «Теория статистики» и пользоваться учебниками, приведенными в списке литературы.
Выполнение домашнего задания имеет важное значение в учебном процессе, так как студенты не только изучают важнейшие методологические вопросы курса, но и приобретают практические навыки при расчетах статистических показателей, построении таблиц и графиков.
Домашнее задание составлено из десяти вариантов.
Номер выполняемого варианта совпадает с последней цифрой номера зачетной книжки. Если последняя цифра – 0 выполняется десятый вариант, какая бы цифра перед ним не стояла.
Каждый вариант домашнего задания состоит из 13 задач по наиболее важным разделам курса. Задачи по вариантам и темам распределяются следующим образом:
| Тема | Вариант задания | |||||||||||||
| I | II | III | IY | Y | YI | YII | YIII | IX | X | |||||
| номера задач | ||||||||||||||
| Средние Величины | №1, №14, №15 | №2, №8, №16 | №3, №11, №17 | №7, №12, №18 | №5, №14, №19 | №4, №9, №20 | №6, №13, №21 | №5, №8, №22 | №4, №10, №23 | №3, №7, №24 | ||||
| Показатели вариации и выборочное наблюдение 1) | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | ||||
| Ряды динамики и прогнозиро- вание | №1, №7, №13, №19 | №2, №8, №14, №20 | №3, №9, №15, №21 | №4, №10, №16, №22 | №5, №11, №17, №23 | №6, №12, №18, №24 | №2, №9, №13, №20 | №4, №11, №14, №23 | №5, №12, №18, №21 | №3,
№7, №16, №19 | ||||
| Индексы | №1, №7, №13, №19 | №2, №8, №14, №20 | №3, №9, №15, №21 | №4, №18, №16, №22 | №5, №11, №17, №23 | №6, №12, №18, №24 | №5, №18, №12, №21 | №6, №8, №15, №22 | №2, №9, №13, №23 | №4, №14, №13, №24 | ||||
| Корреляци- онный метод изучения связи | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | ||||
1) Тема «Выборочное наблюдение» изучается студентами в курсе Теории вероятностей и математической статистики.
Тема: «Средние величины»представлена задачами 1-24.
В задачах 1-14 внимательно подойдите к выбору видов средней. Помните, что форма и вид средней должны отражать экономическое содержание определяемых показателей. Например, средняя себестоимость единицы изделия определяется отношением общих затрат на производство к количеству выпускаемых изделий. Если в условии задачи по цехам (бригадам и т. п.) имеются данные о себестоимости единицы изделия и количестве изделий, то исходя из экономического содержания показателя, для расчета средней себестоимости применяется средняя арифметическая взвешенная:
 ,
,
где х – себестоимость единицы изделия,
f – количество изделий.
Если в условии даны показатели о себестоимости единицы изделия и издержки производства, то для расчета среднего показателя применяется средняя гармоническая взвешенная:
|
|
|

где х – себестоимость единицы изделия,
М – издержки производства.
Пример. Имеются следующие данные по предприятиям акционерного общества, выпускающих однородные изделия:
| № предприятия | I Квартал | II квартал | ||
| Себестоимость ед. изделия, руб. х | Выпуск изделий, тыс. ед. f | Себестоимость ед. изделия, руб. x | Затраты на производство (издержки производства), тыс. руб. M | |
| 1 | 7,5 | 50,0 | 9,0 | 360,0 |
| 2 | 5,4 | 35,0 | 7,0 | 210,0 |
Требуется определить среднюю себестоимость одного изделия в целом по предприятиям за I и II кварталы.
Решение.
Экономическое содержание показателя:
Общие затраты на производство
Средняя (издержки производства)
 себестоимость =
себестоимость =
единицы изделия Количество выпущенных изделий
Для расчета общих затрат на производство изделий необходимо себестоимость ед. изделия (х) умножить на выпуск изделий (f) по предприятиям и просуммировать их.
Средняя себестоимость единицы изделия в I квартале равна:
 ,
,
|
|
|
 (руб.)
(руб.)
Расчеты произведены по формуле средней арифметической взвешенной.
Во II квартале отсутствуют прямые данные о количестве выпущенных изделий, но их можно рассчитать косвенным путем, разделив затраты на производство (М) на себестоимость единицы изделия (x).
Средняя себестоимость единицы изделия во II квартале равна:
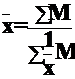 или
или 

Расчеты произведены по формуле средней гармонической взвешенной.
Сравнивая среднюю себестоимость единицы изделия в I и II кварталах, можно отметить, что она возросла на 1,5 рубля (8,14-6,64).
Помимо степенных средних, в статистике применяют особые средние описательного характера – медиану и моду (задачи 15-24). Если все варианты признака расположены в определенном порядке, а именно, либо по их возрастанию, либо по их убыванию, то такой ряд называется ранжированным, то есть упорядоченным. Вариант признака, который занимает в таком ряду срединное положение, называется медианой.
Другими словами, медиана – это срединная величина ранжированного (упорядоченного) вариационного ряда. Если вариационный ряд имеет четное количество членов, то медиана равна полусумме двух срединных вариант.
В случае, если мы имеем интервальный вариационный ряд, то медиана рассчитывается по формуле:
|
|
|

где Xme – нижнее значение интервала, содержащего медиану;
ime – величина медианного интервала;
 – сумма частот ряда;
– сумма частот ряда;
 – номер медианы;
– номер медианы;
 – сумма накопленных частот в интервале, предшествующем медианному.
– сумма накопленных частот в интервале, предшествующем медианному.
 – частота медианного интервала.
– частота медианного интервала.
Пример. Имеются следующие данные о распределении ткачих по дневной выборке:
| Номер группы | 1 | 2 | 3 | 4 | 5 | Итого |
| Дневная выработка, м | до 40 | 40-60 | 60-80 | 80-100 | свыше 100 | |
| Число ткачих | 25 | 30 | 40 | 35 | 20 | 150 |
Требуется рассчитать медиану по дневной выработке ткачих.
Решение.
Чтобы определить медиану, необходимо найти ее порядковый номер (  ), а затем по накопленным частотам или частотам определить тот интервал, в котором находится медиана.
), а затем по накопленным частотам или частотам определить тот интервал, в котором находится медиана.
В нашем примере порядковый номер медианы равен  .
.
Далее следует по накопленным частотам определить интервал, в котором находится медиана. Произведем следующие расчеты:
| Номер группы | Дневная выработка, м | Число ткачих | Накопленные частоты |
| 1 | до 40 | 25 | 25 |
| 2 | 40-60 | 30 | 55 |
| 3 | 60-80 | 40 | 95 |
| 4 | 80-100 | 35 | 130 |
| 5 | свыше 100 | 20 | 150 |
| -- | -- | 150 | -- |
Медианным интервалом является третий интервал: 60-80, так как номер 75 находится именно в этом интервале, судя по накопленным частотам.
Таким образом:
Xme = 60; ime = 80 – 60 = 20;  = 150;
= 150; 
 = 55
= 55  = 40
= 40

Это означает, что первая половина ткачих (50%) имеют дневную выработку меньше 70 м, а вторая – больше.
Мода – вторая описательная характеристика вариационных рядов: это наиболее часто встречающееся значение признака, т.е. значение, которому соответствует наибольшая частота. Если мы имеем интервальный вариационный ряд, то мода определяется по следующей формуле:

где  – начальное значение интервала, содержащего моду;
– начальное значение интервала, содержащего моду;
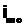 – величина модального интервала;
– величина модального интервала;
 – частота модального интервала;
– частота модального интервала;
 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Пример. Контрольная проверка дневного удоя молока на молочно-товарной ферме дала следующие результаты:
| Номер группы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Дневной удой – кг | менее 3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | более 15 |
| Число коров в группе | 8 | 25 | 50 | 80 | 40 | 22 | 13 | 10 |
Требуется рассчитать моду по дневному удою молока.
Решение.
Чтобы найти моду, необходимо вначале определить модальный интервал. Из примера видно, что наибольшая частота (80) соответствует интервалу 7-9. Это и есть модальный интервал. Мода по дневному удою молока, согласно выше приведенной формуле, рассчитывается следующим образом:
 = 7;
= 7; 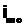 = 9 – 7 = 2;
= 9 – 7 = 2;  = 80;
= 80;  = 50;
= 50;  = 40.
= 40.

По темам«Показатели вариации» и «Выборочное наблюдение» составлены задачи 1-10. Вначале для решения задач необходимо вычислить среднюю арифметическую взвешенную по данным интервального ряда, затем показатели вариации: дисперсию, среднее квадратическое отклонение и коэффициент вариации. Показатель дисперсии (s2) необходим для расчета ошибки выборки, а среднее квадратическое отклонение ( 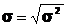 ) – для расчета коэффициента вариации.
) – для расчета коэффициента вариации.
Вторая часть задачи выполняется по теме «Выборочное наблюдение». Необходимо разобраться в понятии повторный и бесповторный отбор, в формулах вычисления предельной ошибки выборки  :
:
для среднего значения признака:
 ;
;  (бесповторный отбор);
(бесповторный отбор);
для доли признака:
 ;
;  (бесповторный отбор).
(бесповторный отбор).
Доверительный интервал для генеральной средней может быть рассчитан следующим образом:
 .
.
Доверительный интервал для доли признака равен:
 .
.
Пример. Для изучения уровня производительности труда рабочих фирмы проведено 2%-ное выборочное обследование по методу случайного бесповторного отбора:
| Дневная выработка, руб. | Число рабочих |
| До 600 | 15 |
| 600-700 | 24 |
| 700-800 | 30 |
| 800-900 | 21 |
| Св. 900 | 10 |
| Итого: | 100 |
По данным выборочного обследования определить:
1) среднюю дневную выработку рабочих фирмы, дисперсию и среднее квадратическое отклонение;
2) коэффициент вариации;
3) с вероятностью 0,997 возможные пределы, в которых находится дневная выработка всех рабочих фирмы;
4) с вероятностью 0,954 возможные границы, в которых находится удельный вес рабочих, дневная выработка которых свыше 900 рублей.
Решение.
Для определения средней дневной выработки рабочих по выборочной совокупности (  ), дисперсии (σ2) и среднего квадратического отклонения (σ) произведем следующие расчеты:
), дисперсии (σ2) и среднего квадратического отклонения (σ) произведем следующие расчеты:
| Дневная выработка, руб. | Число рабочих f (n) | Середина интервала, x | 
| 
| 
|
| До 600 | 15 | 550 | -187 | 34969 | 524535 |
| 600-700 | 24 | 650 | -87 | 7569 | 181656 |
| 700-800 | 30 | 750 | +13 | 169 | 5070 |
| 800-900 | 21 | 850 | +113 | 12769 | 268149 |
| Св. 900 | 10 | 950 | +213 | 45369 | 453690 |
| Итого: | 100 | - | - | - | 1433100 |
1. 





2. Коэффициент вариации рассчитывается по формуле:

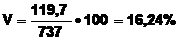 .
.
3. Возможные пределы, в которых находится средняя дневная выработка всех рабочих фирмы, рассчитывается следующим образом:
 , где
, где 
В выборочном наблюдении фактическая ошибка репрезентативности (  ) может быть больше или меньше средней ошибки (μ). Вопрос о пределах возможной ошибки собственно-случайной выборки решается на основе теорем Чебышева и Ляпунова, которые определяют вероятность того, что ошибка репрезентативности (∆) не превзойдет t-кратную среднюю ошибку (μ),т.е. t-раз взятую среднюю ошибку репрезентативности.
) может быть больше или меньше средней ошибки (μ). Вопрос о пределах возможной ошибки собственно-случайной выборки решается на основе теорем Чебышева и Ляпунова, которые определяют вероятность того, что ошибка репрезентативности (∆) не превзойдет t-кратную среднюю ошибку (μ),т.е. t-раз взятую среднюю ошибку репрезентативности.
На основании теоремы Чебышева в формулировке Ляпунова устанавливается, что для t=1 соответствует вероятность р=0,683.
для t=2 соответствует вероятность р=0,954.
для t=3 соответствует вероятность р=0,997.
для t=4 соответствует вероятность р=0,999937 и т.д.
Средняя ошибка выборки (μ) рассчитывается по формуле:
 , где
, где
s2 – средний квадрат отклонения (дисперсия) в выборке;
n – численность выборки;
N – численность генеральной совокупности.
В нашем примере при условии, что проведено 2%-ное обследование, N=5000.

Размер возможной (допустимой) или предельной ошибки выборки рассчитывается по формуле:  ,
,
где t=3 при p=0,997.
Следовательно:  =3·11,85=±35,33 (рубля).
=3·11,85=±35,33 (рубля).
Итак, с вероятностью 0,997 можно утверждать, что средняя дневная выработка всех рабочих фирмы будет находиться в пределах:

4. Возможные пределы (границы), в которых находится удельный вес рабочих фирмы дневная выработка которых свыше 900 рублей, можно рассчитать таким образом:
 ,
,
где  ;
;  ;
;  .
.
Условные обозначения:
W – доля данного признака в выборке;
(1-W) – доля противоположного признака в выборке;
m – количество единиц данного признака в выборке.
Итак,  или 10%
или 10%

 или 2,97%.
или 2,97%.
Предельная ошибка выборки для доли рассчитывается по формуле:
 ,
,
где t=2 при р=0,954.
Следовательно:  с вероятностью 0,954 можно утверждать, что удельный вес всех рабочих фирмы, у которых дневная выработка свыше 900 рублей, находится в пределах:
с вероятностью 0,954 можно утверждать, что удельный вес всех рабочих фирмы, у которых дневная выработка свыше 900 рублей, находится в пределах:
 или
или 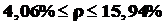 .
.
Тема «Ряды динамики и прогнозирование» представлена задачами 1-24.
В задачах 1- 6 требуется определить аналитические показатели ряда динамики. Особое внимание следует уделить расчету средних показателей ряда динамики.
Средний уровень ряда в задачах 1-6 вычисляется по формуле:

 .
.
Средний абсолютный прирост исчисляется двумя способами:
а) как средняя арифметическая простая цепных приростов
 ,
,
б) делением базисного прироста на число периодов:

В рядах динамики приняты следующие обозначения:
У0 – начальный уровень ряда;
Уi – каждый последующий уровень, начиная со второго;
Уn – конечный уровень ряда.
Темпы динамики (роста или снижения) вычисляются по формулам:

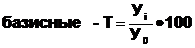
Среднегодовой темп динамики (роста или снижения) исчисляется по формуле средней геометрической двумя способами:

где Т1; Т2...Тn – цепные темпы роста или снижения;
n – число темпов;
П – знак произведения;
ПТ – произведение цепных темпов роста или снижения.
 |
где У0 – начальный уровень;
Уn – конечный уровень;
n – число уровней ряда динамики в изучаемом периоде.
Абсолютное содержание одного процента прироста (1%) исчисляется только в натуральном или денежном выражениях, то есть в абсолютных величинах. Этот показатель может быть исчислен двумя способами:

где Уi-1 – предшествующий уровень ряда;
 – абсолютный прирост;
– абсолютный прирост;
Тпр – темп прироста.
Для характеристики изменения величины во времени может быть использован абсолютный прирост. Абсолютный прирост ( ) показывает, на сколько изменился (возрос или уменьшился) последующий уровень ряда по сравнению с предшествующим или начальным.
) показывает, на сколько изменился (возрос или уменьшился) последующий уровень ряда по сравнению с предшествующим или начальным.
 .
.
Задачи 7-12 составлены на расчет среднего уровня моментного ряда динамики.
Средний уровень моментного ряда динамики с равными интервалами определяется по формуле средней хронологической:
 ,
,
где n — число уровней ряда.
Пример.
На фирме имеются следующие остатки сырья: на 1 января – 242 тыс. руб.; на 1 февраля – 251 тыс. руб.; на 1 марта – 213 тыс. руб.; на 1 апреля – 186 тыс. руб. Определить средний месячный остаток сырья в первом квартале.
Решение.
В условии данные представлены в виде моментного ряда с равностоящими датами, средний уровень ряда определяется по формуле:

Для решения задач 13-24 необходимо изучить наиболее эффективный способ выявления основной тенденции развития явления аналитическое выравнивание с выходом на прогнозирование.
Пример. Имеются данные об объеме реализации продукции некоторыми фирмами Ростовской области за 2002-2010 гг. (млн. руб.):
2002 – 221 2005 – 285 2008 – 360
2003 – 235 2006 – 304 2009 – 371
2004 – 272 2007 – 320 2010 – 295
Для изучения общей тенденции объема реализации продукции произведите аналитическое выравнивание ряда по прямой и, экстраполируя тенденцию, определите показатель в 2015 году.
Решение.
Для выравнивания ряда динамики по прямой используют уравнение:
 .
.
Показателям времени t придают условное значение таким образом, чтобы их сумма была равна нулю, т.е.: 
В данном примере число исходных уровней ряда – нечетное (n=9), условный отсчет (t) в решении производим следующим образом:
| Годы | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| t | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 |
Далее, произведем расчет необходимых показателей:
| Годы | Эмпирические уровни ряда (yi) | Условное обозначение времени (t) | t2 | yit |

|
| 2002 | 221 | -4 | 16 | -884 | 219,32 |
| 2003 | 235 | -3 | 9 | -705 | 241,24 |
| 2004 | 272 | -2 | 4 | -544 | 263,16 |
| 2005 | 285 | -1 | 1 | -285 | 285,08 |
| 2006 | 304 | 0 | 0 | 0 | 307,0 |
| 2007 | 320 | +1 | 1 | 320 | 328,92 |
| 2008 | 360 | +2 | 4 | 720 | 350.84 |
| 2009 | 371 | +3 | 9 | 1113 | 372,76 |
| 2010 | 295 | +4 | 16 | 1580 | 394,68 |
| Итого: | 2763 | 0 | 60 | 1315 | 2763 |
Определим параметры:
 ;
;
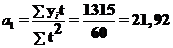
Уравнение общей тенденции ряда динамики:  .
.
Подставляя в уравнение принятые обозначения t, вычисляем выравненные уровни ряда динамики  :
:
2002 г. - 
2003 г. - 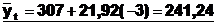 и т.д.
и т.д.
Правильность расчета уровней выравниваемого ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда должна быть близкой или совпадать с суммой вычисленных уровней выравниваемого ряда, т.е.:  .
.
Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Экстраполируя при t=5, находим уровень 2011 г., равный:
 тыс. руб.
тыс. руб.
Уровень 2012 г. при t=6 равен:
 тыс. руб. и т.д.
тыс. руб. и т.д.
Примечание. При четном числе уровней ряда динамики для того, чтобы  , отсчет условного времени производится следующим образом:
, отсчет условного времени производится следующим образом:
| Годы | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| t | -7 | -5 | -3 | -1 | +1 | +3 | +5 | +7 |
и т.д.
По теме «Индексы» составлены задачи 1–24. Задачи 1–6 решаются по агрегатной форме индекса. Методику расчета некоторых общих агрегатных индексов рассмотрим на следующем примере:
Допустим, имеются данные о реализации товаров какой-либо фирмы за два периода.
| Товары | 1 квартал | 2 квартал | ||
| Продано, тыс. кг | Цена 1 кг., руб. | Продано, тыс. кг | Цена 1 кг., руб. | |
| А Б | 42,0 30,0 | 40 30 | 40,0 20,0 | 50 40 |
| q0 | p0 | q1 | p1 | |
1. Определить общие агрегатные индексы:
а) цен по формулам Пааше и Ласпейреса;
б) физического объема товарооборота (в сопоставимых ценах);
в) товарооборота (в фактических ценах).
2. Рассчитать абсолютное изменение общей суммы товарооборота за счет изменения цен и количества реализованных товаров.
3. Показать взаимосвязь между исчисленными индексами.
Решение:
1. а). Агрегатный индекс цен Пааше исчисляется по формуле:


Агрегатный индекс цен Ласпейреса исчисляется по формуле:

По формуле Пааше цены на реализованные фирмой товары во 2 квартале по сравнению с 1-ым выросли в среднем на 27,3% (127,3-100,0), а по формуле Ласпейреса – на 27,9% (127,9-100,0). Индекс Пааше показывает влияние изменения цен на стоимость товаров, реализованных в отчетном периоде, а индекс Ласпейреса – на стоимость товаров реализованных в базисном периоде.
б). Агрегатный индекс физического объема товарооборота (количества проданных товаров) в сопоставимых ценах исчисляется по формуле:

Количество проданных товаров во 2 квартале по сравнению с 1-ым снизилось на 14,7% (85,3-100,0).
в). Агрегатный индекс товарооборота (в фактических ценах) можно вычислить по формуле:

Товарооборот (выручка от продаж) в отчетном периоде по сравнению с базисным, т.е. во 2 квартале по сравнению с 1-ым, возрастает на 8,5% (108,5-100,0).
2. Абсолютное изменение общей суммы товарооборота исчисляется как разность между числителем и знаменателем агрегатного индекса товарооборота:

Прирост товарооборота обусловлен влиянием цен и количества реализованных товаров.
Прирост товарооборота за счет изменения цен по индексу Пааше составил:
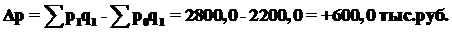
За счет изменения количества проданных товаров произошло снижение товарооборота.

Общее изменение товарооборота равно сумме приростов (снижения) за счет изменения цен и за счет изменения количества продаж. Итак, общий абсолютный прирост товарооборота (Δpq) представлен в данном случае индексной аддитивной моделью (аддитивный – это означает получаемый путем сложения: Δpq=Δp+ Δq).
Сделаем проверку исчисленных показателей. Результат (Δpq) должен быть равен 220,0 тыс.руб.: Δpq = +600,0+(-380,0) = +220,0 тыс.руб. Следовательно, увеличение товарооборота на 220,0 тыс.руб. произошло за счет роста цен на 600,0 тыс.руб. и за счет сокращения количества реализованных товаров на 380,0 тыс.руб.
3. Между исчисленными индексами существует определенная взаимосвязь, которая может быть представлена индексной мультипликативной моделью.
Индекс представляет собой мультипликативную модель, ели он может быть рассчитан в виде произведения двух, как в нашем примере, или нескольких определяющих его индексов:

Следует заметить, что если индекс цен рассматривается в системе с индексом физического объема и индексом товарооборота, то он должен вычисляться по формуле Пааше.
Любой недостающий индекс можно определить, пользуясь формулой взаимосвязи индексов.
Это можно подтвердить следующими расчетами. Определяем индекс цен: 
Определяем индекс физического объема товарооборота:

В задачах 7-9, 14, 17, 18 применяется средний арифметический индекс, который определяется для количественных показателей. Примером может служить индекс физического объема товарооборота:

Этот индекс тождествен (равен) агрегатному индексу, который вычисляется по формуле:
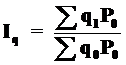 .
.
Рассмотрим методику определения среднего арифметического индекса физического объема продукции по следующим данным:
| Наименование товарных групп | Выручка от реализации в базисном периоде, тыс. руб. | Индивидуальный индекс физического объема товарооборота |
| P0q0 | iq | |
| I | 20,0 | 1,47 |
| II | 30,0 | 1,55 |
| III | 25,0 | 1,71 |
| IV | 15,0 | 2,10 |
| Итого | 90,0 | - |
Рассчитаем средний арифметический индекс физического объема товарооборота по четырем товарным группам:

или 166,7%.
Физический объем продажи по четырем товарным группам увеличился на 66,7% (166,7% - 100%).
Задачи 10-13, 15, 16 составлены на использование среднего гармонического индекса, который определяется для качественных показателей (цен, себестоимости, заработной платы, трудоемкости и т. п.). Примером может служить индекс цен:
 .
.
Этот индекс тождествен агрегатному индексу:

Покажем расчет среднего гармонического индекса цен и других индексов, используя следующие данные:
| Объем товарооборота, тыс. руб. | |||
| Изделия | I квартала P0q0 | II квартала P1q1 | Индивидуальный индекс цен, ip |
| I | 750 | 780 | 1,05 |
| II | 530 | 520 | 1,03 |
| III | 315 | 340 | 1,11 |
| Итого | 1595 | 1640 | |
Исчислим средний гармонический индекс цен:
 или 105,53%.
или 105,53%.
Цены в среднем возросли на 5,53% (105,53%-100%).
Общий индекс товарооборота:
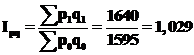 или 102,9%.
или 102,9%.
Общий индекс физического объема товарооборота определим по формуле взаимосвязи индексов: 
 или 97,5%.
или 97,5%.
Общий товарооборот увеличился на 2,9%, а физический объем продажи снизился на 2,5%.
В задачах 5, 14, 15 необходимо использовать различные формы индексов общих затрат рабочего времени, трудоемкости и производительности труда, которые приведены ниже.
Общий индекс затрат рабочего времени (затрат труда) вычисляется по формуле:

где  – общие затраты рабочего времени в отчетном периоде;
– общие затраты рабочего времени в отчетном периоде;
 – общие затраты рабочего времени в базисном периоде.
– общие затраты рабочего времени в базисном периоде.
Общий индекс трудоемкости единицы продукции исчисляется по формуле:

где:  – условные общие затраты рабочего времени в отчетном периоде.
– условные общие затраты рабочего времени в отчетном периоде.
Индекс трудоемкости можно также рассчитать следующим образом, используя формулу среднегармонического индекса:

Общий индекс производительности труда по затратам рабочего времени вычисляется по формуле:

Этот индекс является обратной величиной по отношению к индексу трудоемкости:
 .
.
Для расчета индекса производительности труда можно воспользоваться среднеарифметической формой индекса:

В задачах 19-25 необходимо определить индексы переменного и постоянного составов, а также индекс структурных сдвигов.
Индекс постоянного состава вычисляется по формуле:
 .
.
Данный индекс изменяется под влиянием только индексируемой величины.
Индекс переменного состава вычисляется как отношение двух средневзвешенных величин с переменными весами. Его можно представить в следующем виде:

где, х1 и х0 — уровни показателя соответственно в отчетном и базисном периодах;
f1 и f0 — веса в отчетном и базисном периодах.
Индекс переменного состава изменяется под влиянием двух факторов: изменения индексируемой величины и структуры. Индекс структурных сдвигов вычисляется по формуле:

Рассмотрим расчет показателей на следующем примере:
Динамика таможенного тарифа на экспортируемую продукцию фирмой «Конус»:
| Вид продукции | I квартал | II квартал | ||
| Тарифная ставка, % х0 | Сумма экспорта, долл. f0 | Тарифная ставка, % х1 | Сумма экспорта, долл. f1 | |
| А | 0,9 | 8240,0 | 0,96 | 8927,0 |
| Б | 0,07 | 11,2 | 0,10 | 14,3 |
| В | 22,0 | 51296,1 | 24,5 | 7456,3 |
Определить:
1) индекс таможенного тарифа постоянного состава;
2) Индекс таможенного тарифа переменного состава;
3) Индекс структурных сдвигов.
Вычислим индекс постоянного состава по формуле:

Увеличение в среднем таможенного тарифа на 11,1% (111,1% - 100%) зависит от изменения тарифной ставки во II квартале по сравнению с I кварталом.
Определим изменение среднего таможенного тарифа за I и II кварталы:


Вычислим индекс таможенного тарифа переменного состава по формуле:  или 61,2%.
или 61,2%.
Следовательно, за счет влияния тарифной ставки и сдвигов в структуре экспорта средний таможенный тариф снизился на 38,9% (100%-61,1%).
Индекс структурных сдвигов составил:
Iстр. сдвг. =Iперем. сост. / Iпост. сост. =0,611÷1,111=0,550 или 55,0%.
Изменение структуры экспорта во II квартале повлекло снижение таможенного тарифа дополнительно на 45,0% (100%-55,0%).
 Тема «Корреляционный метод изучения связи» представлена задачами 1-10, в которых требуется вычислить линейное уравнение связи и коэффициенты тесноты связи между заданными признаками. Для их решения необходимо внимательно изучить соответствующий материал по учебникам.
Тема «Корреляционный метод изучения связи» представлена задачами 1-10, в которых требуется вычислить линейное уравнение связи и коэффициенты тесноты связи между заданными признаками. Для их решения необходимо внимательно изучить соответствующий материал по учебникам.
Уравнение связи в общем виде: 
Параметры уравнения связи а0 и а1 могут быть определены различными способами. Линейный коэффициент корреляции (коэффициент тесноты связи) также имеет несколько способов расчета. Студент может выбрать любой из них:
 или
или 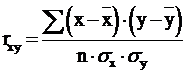 ,
,
а также 
Ниже приведен расчет коэффициента корреляции по данным об оборачиваемости оборотных средств (количество оборотов)и уровне рентабельности:
| Количество оборотов x | Уровень рентабельности, %, y | xy | x2 | y2 |
| 1 | 17,0 | 17,0 | 1 | 289,0 |
| 2 | 20,0 | 40,0 | 4 | 400,0 |
| 3 | 25,0 | 75,0 | 9 | 625,0 |
| 4 | 28,0 | 112,0 | 16 | 784,0 |
| 5 | 34,0 | 170,0 | 25 | 1156,0 |
| Итого: 15 | 124,0 | 414,0 | 55 | 3254,0 |
Отсюда:
 .
.
Для характеристики тесноты связи между признаками можно воспользоваться таблицей, предложенной американским ученым Чэддоком:
| Величина показателя тесноты связи | Сила связи |
| 0,1 - 0,3 | слабая |
| 0,3 - 0,5 | умеренная |
| 0,5 - 0,7 | заметная |
| 0,7 - 0,9 | высокая |
| 0,9 - 0,99 | очень высокая |
1. Согласно таблице связь между количеством оборотов (х) оборотных средств и уровнем рентабельности (у) прямая и очень высокая (rху = 0,99).
Однако, сама величина коэффициента корреляции еще не доказывает достоверность связи между исследуемыми факторами, поэтому его требуется проверить на значимость. Существует множество способов оценки существенности линейного коэффициента корреляции.
Значимость коэффициента корреляции можно проверить при помощи статистики t, которая имеет следующую формулу:

где: rxy – проверяемый линейный парный коэффициент корреляции,
srxy – стандартная ошибка коэффициента корреляции.
Стандартная ошибка при малом числе наблюдений, т.е. если n<30, рассчитывается по формуле:
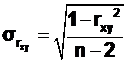 .
.
Применительно к нашему примеру:


Следовательно, можно сделать вывод о значимости коэффициента корреляции, связь между факторами не случайна, т.к. t=12,2, т.е. t > 3
2. Параметры уравнения прямой  можно определить по следующим формулам:
можно определить по следующим формулам:
 ;
;
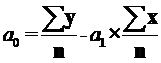 .
.
Для нашего примера:


В соответствии с произведенными расчетами а0=12,2; а1=4,2. Следовательно уравнение регрессии может быть записано следующим образом:

Коэффициент регрессии (а1 при x) показывает, что с увеличением количества оборотов оборотных средств (x) на единицу, уровень рентабельности (y) в среднем возрастает на 4,2%.
Свободный член уравнения (а0) равен 12,2. Это может означать, что на величину рентабельности могут влиять другие, неучтенные факторы.
Дата добавления: 2018-02-15; просмотров: 635; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
