Показатели центра распределения

Для характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая, медиана, мода.

Средняя арифметическая для дискретных иинтервальныхрядов распределения исчисляется по формуле:

(5.9)

где — варианты значений признака. В случае непрерывного значения признака в качестве принимаетсясередина соответствующего интервала и вычисляется как средняя из значений границ интервала.

Медиана (Me) соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером:

, (5.10)

где n — число единиц в совокупности.

По накопленным частотам определяют ее местоположение и численное значение в дискретном вариационном ряду.

Если совокупность содержит четное число значений варьирующего признака (n = 2k; k = n/2), то в этом случае за медиану условно принимают значение

, (5.11)

так как в ряду нет члена, который делил бы совокупность на две равные по объему группы.

В интервальном ряду распределения сначала указывают интервал, в котором находится медиана.

Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.

Мода (Мо) — наиболее часто встречающееся значение признака. В дискретном ряду — это варианта с наибольшей частотой. В интервальном ряду сначала определяется модальный интервал, т. е. тот интервал, который имеет наибольшую частоту.

Численное значение моды и медианы определяется по формулам:

(5.12)

(5.13)

где - нижние границы модального и медианного интервалов;

- ширина модального и медианного интервалов;

- частость модального интервала;

- частость интервала, предшествующему модальному;

- частость интервала следующего за модальным;

- половина суммы накопленныхчастостей (равна 0,5);

- накопленнаячастость до медианного интервала;

- частость медианного интервала.

Моду и медиану можно определить на основе графического изображения ряда. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной.

Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника — с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Показатели вариации признака

Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся:

• размах колебаний;

• среднее линейное отклонение;

• среднее квадратическое отклонение;

• дисперсия;

• квартильное отклонение.

Формулы расчета абсолютных показателей вариации следующие:

Размах вариации:

,(5.14)

где соответственно максимальное и минимальное значения признака.

Среднее линейное отклонение:

.(5.15)

Дисперсия:

. (5.16)

Среднее квадратическое отклонение:

. (5.16) Формулы расчета относительных показателей вариации следующие:

Коэффициент осцилляции:

. (5.18)

Линейный коэффициент вариации:

. (5.19)

Коэффициент вариации:

. (5.20)

Относительный показатель квартильной вариации:

, (5.21) где 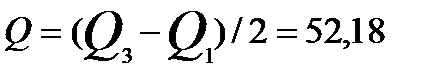- среднее квартильное расстояние;

; (5.22)

; (5.23)

- соответственно первая и третья квартили распределения;

- нижние границы интервалов, в которых находятся первая и третья квартили;

- ширины интервалов первой и третьей квартили;

и - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;

- частости интервалов, в которых находятся первая и третья квартиль.

В практике из показателей вариации получили широкое применение дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Сложение дисперсий изучаемого признака.

Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих вариацию индивидуальных значений (вариант) признака. Это можно сделать при помощи метода группировок, когда единицы изучаемой совокупности подразделяются на однородные группы по признаку- фактору. При этом, кроме общей средней для всей совокупности, исчисляются средние по отдельным группам (групповые или частные средние) и три показателя дисперсии:

• общая дисперсия;

• межгрупповая дисперсия;

• средняя внутригрупповая дисперсия.

Величина общей дисперсии ( ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле:

,(5.24)

где — общая средняя арифметическая для всей изучаемой совокупности.

Межгрупповая дисперсия отражает систематическую вариацию, т. е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки (графа 14 табл. 5.2). Межгрупповая дисперсия определяется по формуле:

,(5.25)

где , — средняя по отдельной группе (графа 13 табл. 5.2);

, — число единиц в определенной группе.

Средняя внутригрупповая дисперсия ( ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.

Средняя внутригрупповая дисперсия определяется по формуле:

,(5.26)

где —дисперсия в j-ой группе (графа 14 табл. 5.2), вычисляемая по формуле:

. (5.27)

Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

.(5.28)Это тождество отражает закон (правило) сложения дисперсий. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака- фактора, положенного в основу группировки.

Вариация альтернативного признака.

Альтернативный признак - качественный признак, имеющий две взаимоисключающие разновидности (например, работники предприятия подразделяются на мужчин и женщин; продукция — на годную и бракованную и т. д.).

Альтернативный признак принимает всего два значения:

1 — наличие признака;

0 — отсутствие признака.