Лекция №5. Необходимые математические представления о сигнале

Математическое представление сигнала

В предыдущей главе мы показали преобразование изменяющегося во времени аналогового сигнала f (t) при соответствующем интервале дискретизации и представлении выборок в цифровой форме. При малом интервале дискретизации можно достаточно точно воспроизвести первоначальный аналоговый сигнал по цифровому сигналу. Если временной интервал [a;b] разделить на одинаковые отрезки, а сигнал ʃ, уже подвергшийся дискретизации, перевести в цифровую форму и записать в виде ряда значений N точек

f = (f ₁,f₂,……,f_N)

то f представить N – мерным вектором (N-мерным вектором называется величина, представленная набором числовых значений N, расположенных в определённом порядке). Элемент из этого числового набора называется компонентной вектора.

Качество приближения функции f(t) меняется в зависимости от числа N. Если N увеличивать, то степень приближения заметно улучшается. Если увеличивать N до бесконечно большого числа, то вся информация, содержащаяся в f(t) , будет содержаться в f (Рис.3.1.) Это означает, что, в сущности, анализ вектора f вместо функции f(t) (если она не является «особой» , т.е имеет точек разрыва) аналогичен анализу непрерывно изменяющегося во времени сигнала f(t).

Двумерный вектор, расположенный в двумерном пространстве, или, иначе говоря, на плоскости, соответствует какой-либо одной точке на этой плоскости. (Рис. 3.2).

Трёхмерный вектор соответствует одной точке в трёхмерном пространстве, а N- мерный вектор также соответствует одной точке, но N-мерного пространства (к сожалению, изобразить это мы не можем). Если представить пространство бесконечно большой размерности N, то можно предположить, что непрерывная функция f(t) соответствует одной точке этого пространства. Назовём это невидимое абстрактное пространство бесконечной размерности пространством функции.

При размерности векторного пространства N >2 также можно определить, расстояние между векторами и скалярное произведение. Более того, если рассуждать подобным образом, то же самое можно сделать и для пространства функций. Одним словом, давая определение расстоянию и скалярному произведению в пространстве функций, можно говорить о величине и угле между функциями. Вскоре мы будем использовать понятие взаимно перпендикулярных функций, и представлять их в виде взаимно перпендикулярных векторов. В этом случае при внешней сложности формул, станет понятно, что концепция, заключающаяся в использовании векторного расстояния и скалярного произведения для пространства функций , очень проста. Читатель может задать вопрос , какое отношение может иметь данная концепция к обработке сигналов? Дело в том, что при обработке сигналов мы будем оперировать такими понятиями как функция корреляции и анализ Фурье, а они как раз основаны на использовании свойств расстояния и скалярного произведения при переходе от векторного пространства к пространству функции.

Скалярное произведение и расстояние для двумерных векторов

Сделав выборку некоторого сигнала f(t), возьмём из неё два значения f₁и f₂. Таким же образом получим два значения для некоторого сигнала g(t).

Что нужно для того, чтобы узнать степень взаимоотношения между двумя сигналами f(t) и g(t), выходя из их значений? Если сделать выборку, состоящую всего лишь из двух значений, то, естественно, степень приближения к первоначальному сигналу не высока. Как было изложено ранее, эта проблема разрешится, если увеличить число элементов выборки. Но пока рассмотрим случай выборки из двух точек.

Итак, определим векторы, содержащие по два элемента из выборки каждого сигнала, иначе говоря, двумерные векторы.

Обозначим их как f и g:

f = ( f_1;f₂) g = (g₁;g₂).

Если сигналы выразить через векторы таким образом , то исследование отношений между ними есть исследование отношений между векторами. В чём же заключается такое исследование? Во-первых нужно выяснить, насколько удалены векторы f и g т.е. измерить расстояние между векторами (Рис.3.4 ) . Пусть d(f;g)-расстояние между векторами f и g. Чем меньше значение d, тем ближе векторы f и g, а значит и сильнее, взаимосвязь между ними.

Используя компоненты вектора f , получим:

(3.1)

||f||называют также нормой вектора f.

Итак, из рисунка видно, что расстояние между векторами f и g есть норма вектора f-g. Это можно записать, используя компоненты векторов, в следующем виде:

(3.2)

Расстояние – это один из параметров, изменяющих силу связи между векторами. Однако посмотрите на Рис.3.5. На этом рисунке векторы g и h одинаково удалены от вектора f. Но векторы g и f имеют одно и тоже направление, а вектор h расположен под углом к вектору f. Поэтому, увеличив вектор в несколько раз, можно получить вектор g и невозможно получить вектор h. Несмотря на равноудалённость

Рис.3.4 Расстояние и скалярное произведение двумерных векторов g и h от вектора f, связь f и g гораздо сильнее. Видимо, было бы недостаточно выражать связь между векторами одним лишь расстоянием. Необходимо также учитывать угол между ними. (Рис.3.5).

Для выражения связи между векторами используют скалярное произведение между f и g обозначается как (f, g) и определяется как:

Следовательно,

Обозначим эту величину

, следовательно

. Величина r выражает силу связи между векторами f и g через угол между ними (Рис.3.6.). Если направление f и g cсовпадают, то r принимает максимальное значение, равное 1. С увеличением угла f значение r уменьшается. Если r=0, т.е. (f, g)=0

Векторы f и g взаимно перпендикулярны. Назовём величину r коэффициентом корреляции. Как видно из соотношения (3.4), r зависит от угла между векторами и не зависит от нормы векторов.

Как выразить скалярное произведение, используя компоненты вектора? Это можно сделать следующим образом:

Чтобы вывести эту формулу, применим теорему косинусов для векторов (Рис. 3.4):

Следовательно,

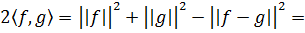
Кстати, скалярное произведение вектора f на самого себя равно:

(3.6)

И выражает связь между скалярным произведением и нормой.

Подставим полученные результаты в выражение коэффициента корреляции (3.4) и представим r следующим образом:

(3.7)

Ортонормированный базис:

Для определения одномерных величин достаточно одного параметра. Например, при измерении длины используют один стандарт величины (сантиметры, миллиметры). Если принять, что 1 см – единица измерения, то 5 см больше 1 см в 5 раз, следовательно, выражается как 5 единиц. Также и в векторном пространстве принято выбирать единицу измерения, которая выражает стандарт величины. Однако в двумерном пространстве одного параметра, измеряющего величину, недостаточно. Необходимо два параметра.

Пара взаимно перпендикулярных векторов {v₁;v₂} называется ортогональным базисом. Кроме того, если ||v₁||=||v₂||=1, то эта пара называется ортогональным базисом. Вектор с нормой, равной 1, называется единичным вектором. Иначе говоря, единичный вектор-это вектор, выражающий величину одной единицы измерения. Следовательно, ортонормированный базис представляет собой пару взаимно перпендикулярных единичных векторов, которые в совокупности с парой параметров дают величину вектора.

Выразим вектор f через векторы ортонормированного базиса v_1,v₂ и совокупность коэффициентов C₁,C₂(Рис.3.7.).

Выражение вектора через ортонормированный базис

Коэффициенты (С₁,С₂) выражают величину составляющих вектора f в направлении v₁ в направлении v₂_.Иначе говоря, определяют величину вектора. Любой вектор на плоскости можно выразить через это соотношение. Векторы C₁v₁ и C₂v₂ называют проекциями вектора f.

Дата добавления: 2018-02-15; просмотров: 847; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒

Мы поможем в написании ваших работ!