ФОРМИРОВАТЕЛЬ МОДУЛИРУЮЩИХ СИМВОЛОВ
Требуется:
1. Изобразить сигнальное созвездие для заданного вида модуляции.

Рис. 9. Сигнальное созвездие для КАМ-16
2. Изобразить график реализации случайного процесса C(t) на входе блока ФМС (выходе сверточного кодера)для первых 16 бинарных интервалов. Написать аналитическое выражение для случайного процесса  .
.

1 1 1 0 0 0 1 0 1 1 0 0 1 1 0 1
Рис. 10. Осциллограмма реализации  с выхода сверточного кодера
с выхода сверточного кодера
Длительность бинарного интервала:

Аналитическое выражение для С(t):
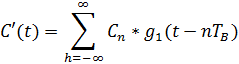
где

3. В соответствии с сигнальным созвездием модулятора КАМ-16 или КФМ-4 изобразить для входной реализации  графики реализаций
графики реализаций  и
и  на выходе блока ФМС случайных процессов
на выходе блока ФМС случайных процессов  и
и  на символьных интервалах длительностью
на символьных интервалах длительностью 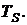 Написать аналитические выражения для случайных процессов
Написать аналитические выражения для случайных процессов 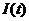 и
и 


где
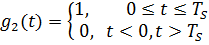
Длительность символьного интервала:


Рис. 11.  Реализация процесса I(t)
Реализация процесса I(t)
Рис. 12. Реализация процесса Q(t)
4. Написать аналитические выражения для корреляционной функции  и спектральной плотности мощности
и спектральной плотности мощности  входного случайного процесса
входного случайного процесса  и построить графики этих функций.
и построить графики этих функций.
Процесс C(t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид:
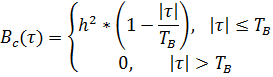

Рис. 13. График корелляционной функции 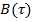
а энергетический спектр



 0
0 

|
|
|
Рис. 14. График энергетического спектра 
5. Написать аналитические выражения для корреляционных функций  и
и  , спектральных плотностей мощности
, спектральных плотностей мощности  и
и  случайных процессов
случайных процессов 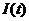 и
и  Построить графики этих функций.
Построить графики этих функций.
Корреляционная функция  случайного процесса
случайного процесса 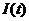 будет соответствовать структуре корреляционной функции
будет соответствовать структуре корреляционной функции  случайного процесса
случайного процесса 

Случайный процесс  имеет такие же вероятностные характеристики, какие имеет процесс
имеет такие же вероятностные характеристики, какие имеет процесс 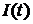 , поэтому имеет место равенство
, поэтому имеет место равенство


Рис. 15. График коррелляционной функции  и
и 
Используя теорему Винера–Хинчина и равенство  , получим
, получим

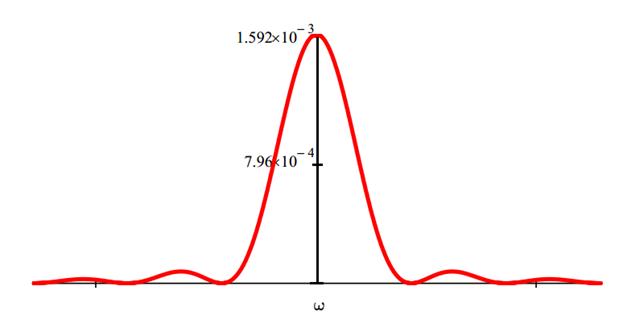
Форма графика функций  и
и  будет похожа на форму графика
будет похожа на форму графика 

 0
0 

Рис. 16. График энергетического спектра  и
и 
6. Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала.
|
|
|
МОДУЛЯТОР
 В состав модулятора входят блоки-перемножители, инвертор и сумматор,на выходе которого получаем сигнал заданного вида модуляции КАМ-16.
В состав модулятора входят блоки-перемножители, инвертор и сумматор,на выходе которого получаем сигнал заданного вида модуляции КАМ-16.
Рис. 17. Схема квадратурно-амплитудного модулятора КАМ-16
В состав модулятора входят блоки:
- генератор несущего колебания UcosωСt,
- фазовращатель на – 90º для получения квадратурного несущего колебания UsinωСt,
- перемножители, для получения БМ сигналов SI(t) =I(t)cosωСtи SQ(t) =Q(t)sinωСt, модулированных сигналами I(t) и Q(t), соответственно;
- сумматор для получения сигнала с квадратурной модуляцией
SКАМ(t)= SI(t) +SQ(t) = I(t)cosωСt + Q(t)sinωСt =
= A(t)cos(ωСt – ψ) = A(t)cos(ωСt + φ),
где  –огибающая, а φ = (–ψ)– фаза сигнала SКАМ(t);
–огибающая, а φ = (–ψ)– фаза сигнала SКАМ(t);
cosψ = I(t)/A(t) = cosφ, sinψ = Q(t)/A(t) = –sinφ.
Требуется:
1. Построить графики гармонических колебаний  и
и 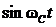 на четырех символьных интервалах
на четырех символьных интервалах 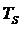 (
(  ). При этом на символьном интервале длительностью
). При этом на символьном интервале длительностью  укладывается два периода частоты
укладывается два периода частоты  .
.




Рис. 18. Графики функций  и
и 
2. На этих же интервалах  нарисовать графики сигналов
нарисовать графики сигналов
 ;
;
 ;
;


Рис. 19. График функции 

 Рис. 20. График функции
Рис. 20. График функции 
|
|
|
Рис. 21. График функции 
 3. На этих же интервалах
3. На этих же интервалах  изобразить график сигнала заданной
изобразить график сигнала заданной
квадратурной модуляции  на выходе сумматора в
на выходе сумматора в
квазигармонической форме, выделив из полученной суммы четыре слагаемых с номерами  .
.
Рис. 22. График функции 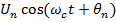
4. Написать аналитические выражения для корреляционных функций  ,
,  для случайных сигналов
для случайных сигналов 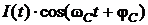 и
и  на выходах перемножителей, где
на выходах перемножителей, где  случайная фаза с равномерной плотностью вероятности на интервале
случайная фаза с равномерной плотностью вероятности на интервале  . Случайная фаза
. Случайная фаза  не зависит от случайных процессов
не зависит от случайных процессов 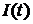 и
и  .
.
Выражения для корреляционных функций имеют вид:


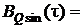


5. Написать аналитические выражения для корреляционной функции сигнала 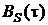 и для спектральной плотности мощности
и для спектральной плотности мощности  сигнала
сигнала 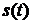 заданного вида квадратурной модуляции на выходе сумматора. Построить графики этих функций.
заданного вида квадратурной модуляции на выходе сумматора. Построить графики этих функций.
Выражение для корреляционной функции имеет вид:


 ,
,



Рис. 23. График функции 
Выражение для спектральной плотности мощности имеет вид:
 .
.

Рис. 24. График функции 
НЕПРЕРЫВНЫЙ КАНАЛ
Передача сигнала  происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид
происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид
|
|
|

где  – коэффициент передачи канала. Для всех вариантов
– коэффициент передачи канала. Для всех вариантов 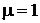 . Односторонняя спектральная плотность мощности помехи равна
. Односторонняя спектральная плотность мощности помехи равна  , (значения
, (значения  для своего варианта в исходных данных).
для своего варианта в исходных данных).
Требуется:
1. Определить минимально необходимую ширину полосы частот непрерывного канала  .
.
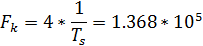
2. Определить мощность помехи  на выходе канала.
на выходе канала.
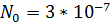

3. Определить 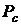 среднюю мощность сигнала
среднюю мощность сигнала  , определить защищённость сигнала по мощности АВ найти отношение
, определить защищённость сигнала по мощности АВ найти отношение 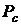 /
/  .
.


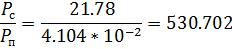
4. Рассчитать пропускную способность  (за секунду) непрерывного канала.
(за секунду) непрерывного канала.

5. Оценить эффективность использования пропускной способности непрерывного канала.


ДЕМОДУЛЯТОР
Когерентный демодулятор производит анализ принятого приёмником смеси переданного сигнала с помехой z(t) = μsКАМ(t) + n(t), сопоставляя его с известными образцами сигналов, формируемых модулятором. Анализ завершается принятием решения по критерию максимального правдоподобия в пользу наиболее вероятного передаваемого сигнала (символа).
Требуется:
1. Изобразить структурную схему когерентного демодулятора,
оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции .

Рис. 25. Схема, реализующая выполнение алгоритма когерентного демодулятора
2. Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора.
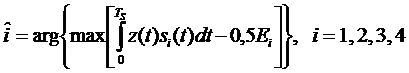 .
.
В момент окончания каждого символьного интервала длительностью  решающее устройство РУ1 (и РУ2) определяет номер входа
решающее устройство РУ1 (и РУ2) определяет номер входа  , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате:
, на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате:
«00» при  = 1, «10» при
= 1, «10» при  = 2, «01» при
= 2, «01» при  = 3, «11» при
= 3, «11» при  = 4.
= 4.
3. Определить вероятности ошибок на выходах РУ1 и РУ2 при определении значений символов  и
и  , равных
, равных 
 =
=  =
=  =
= 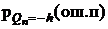 ;
;
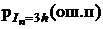 =
=  =
=  =
=  ,
,
где PIn=x(ош) иPQn=x(ош)– вероятности ошибочного приемапри In=h и Qn=h, соответственно
| Передаваемые величины In и Qn | Вероятность ошибки в работе РУ1 и РУ2 |
| In= ±h,Qn= ±h |  ,
гдеQ(x)– дополнительная функция ошибок,
Е1 - энергия сигнала 1·cosωct, Е1 = 0,5·12·TS
NO – спектральная плотность мощности БГШ ,
гдеQ(x)– дополнительная функция ошибок,
Е1 - энергия сигнала 1·cosωct, Е1 = 0,5·12·TS
NO – спектральная плотность мощности БГШ
|
In= ±3h,Qn= ±3h 
| 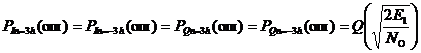
|
Табл. 3. Нахождение вероятности ошибок в работе РУ1 и РУ2
E1 = 0,5h2TS =1.592*10-4

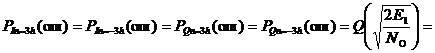
4. Определить вероятности ошибок на выходе преобразователя
параллельного кода в последовательный код (ФМС) для заданных параметров сигналов  и
и  [2]:
[2]:
для точек сигнального созвездия с координатами In= ±h,Qn= ±h (4 точки у QPSKи у QASK)
PIn=h,Qn=h(ош) = PIn=h(ош) + PQn=h(ош) – PIn=h(ош)·PQn=h(ош)=
для точек сигнального созвездия с координатами In= ±3h,Qn= ±3h(4 точки только у QASK)
PIn=3h,Qn=3h(ош) = PIn=3h(ош) + PQn=3h(ош) – PIn=3h(ош)·PQn=3h(ош)=
для точек сигнального созвездия с координатами In= ±3h,Qn= ±h и In= ±h,Qn= ±3h(8 точек только у QASK)
PIn=3h,Qn=h(ош) = PIn=3h(ош) + PQn=h(ош) – PIn=3h(ош)·PQn=h(ош)=
ДЕКОДЕР
Декодер формирует из непрерывной последовательности кодовых символов, поступающих с выхода демодулятора (возможно, с ошибками), выходную непрерывную последовательность декодированных кодовых символов, в которых ошибки частично либо полностью исправлены.
Требуется:
1. Построить решетчатую диаграмму декодера последовательности 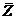 . Численные обозначения над ребрами решетчатой диаграммы определяются для последовательности
. Численные обозначения над ребрами решетчатой диаграммы определяются для последовательности 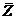 своего варианта.
своего варианта.
Последовательность информационных символов, поступивших на вход кодера:

Последовательность кодовых символов с выхода кодера, которая передавалась по каналу:

Принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера при номере тактового интервала ошибки  :
:


Рис. 26. Решетчатая диаграмма декодера для последовательности 
Решетчатая диаграмма декодера на рис. 26 отличается от решетчатой диаграммы кодера на рис. 7 тем, что ребрам этих решеток соответствуют разные обозначения. Числа над ребрами решетки декодера определяются, как расстояние Хемминга между двумя символами принятой последовательности  , расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера.
, расположенными над данным ребром и двумя символами, которыми отмечено данное ребро на решетке кодера.

 2. Построить диаграммы выживших путей от момента времени
2. Построить диаграммы выживших путей от момента времени  до момента времени
до момента времени  , когда от момента
, когда от момента  до момента
до момента 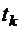 выживает только один путь.
выживает только один путь.
Рис. 27, а. Диаграмма декодера и выжившие пути на интервале t1–t4
Метрики путей:









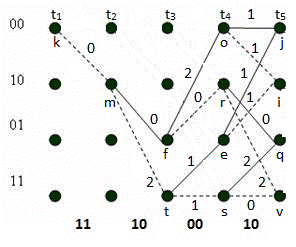 Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов выжившим считается только один путь - тот путь, которому соответствует меньшая метрика. Таким образом выживают пути
Целью алгоритма Витерби является то, что из двух путей, приходящих в каждый из узлов выжившим считается только один путь - тот путь, которому соответствует меньшая метрика. Таким образом выживают пути  ;
; 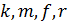 ;
;  ;
;  .
.
Рис. 27, б. Диаграмма декодера и выжившие пути на интервале t1–t5
Метрики путей:








 Выжившие пути:
Выжившие пути:  ;
;  ;
;  ;
;  .
.

Рис. 27, в. Диаграмма декодера и выжившие пути на интервале t1–t6
Метрики путей:


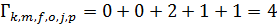
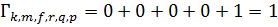




Выжившие пути:  ;
;  ;
; 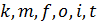 ;
;  .
.


Рис. 27, г. Диаграмма декодера и выжившие пути на интервале t1–t7
Метрики путей:

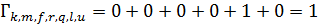






Двум путям, приходящих в узел w, соответствуют одинаковые расстояние Хемминга, равные 3. Поэтому из этих двух путей произвольно выбираем любой, например,  . Таким образом выживают пути
. Таким образом выживают пути  ;
;  ;
;  ;
;  .
.


Рис. 27, д. Диаграмма декодера и выжившие пути на интервале t1–t8
Метрики путей:







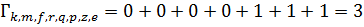
Выжившие пути:  ;
; 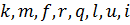 ;
;  ;
;  .
.

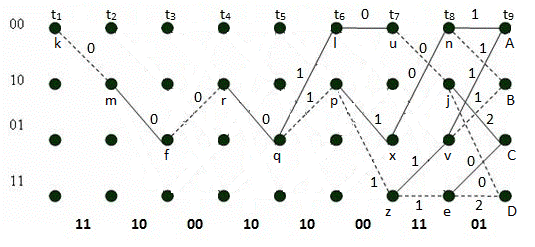
Рис. 27, е. Диаграмма декодера и выжившие пути на интервале t1–t9
Метрики путей:


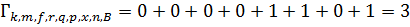



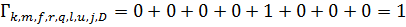

Выжившие пути:  ;
;  ;
;  ;
;  .
.


Рис. 27, ж. Диаграмма декодера и выжившие пути на интервале t1–t10
Метрики путей:


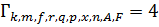

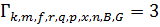


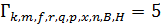
Выжившие пути:  ;
;  ;
;  ;
;  .
.
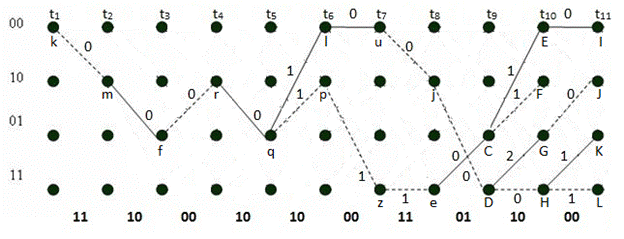
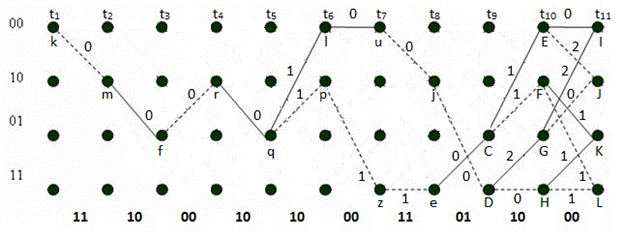
Рис. 27, з. Диаграмма декодера и выжившие пути на интервале t1–t11
Выжившие пути:  ;
;  ;
;  ;
;  .
.

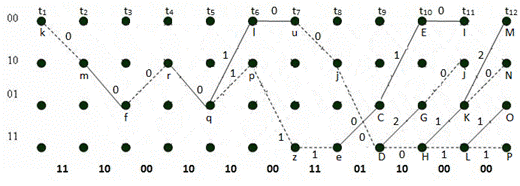
Рис. 27, и. Диаграмма декодера и выжившие пути на интервале t1–t12
Выжившие пути:  ;
;  ;
;  ;
;  .
.
3. Перенести один выживший путь от момента времени  до момента
до момента  с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы,которые поступали на вход сверточного кодера и передавались по каналу связи от момента
с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы,которые поступали на вход сверточного кодера и передавались по каналу связи от момента  до момента
до момента  ,соответствующие принятым кодовым символам с учетом исправленной ошибки. Проследить по диаграмме, что ошибка,отмеченная галочкой, исправлена.
,соответствующие принятым кодовым символам с учетом исправленной ошибки. Проследить по диаграмме, что ошибка,отмеченная галочкой, исправлена.
 Из построенной на рис. 23, и. диаграммы видно ,что от момента t1 до момента t10 выжил только один путь
Из построенной на рис. 23, и. диаграммы видно ,что от момента t1 до момента t10 выжил только один путь  . Теперь перенесем этот один выживший путь с диаграммы декодера на диаграмму кодера. Этому пути на диаграмме кодера соответствуют обозначения ребер 11,10,00,10,11,00,11,01,10.
. Теперь перенесем этот один выживший путь с диаграммы декодера на диаграмму кодера. Этому пути на диаграмме кодера соответствуют обозначения ребер 11,10,00,10,11,00,11,01,10.
Рис. 28. Путь, соответствующий кодовым символам
Декодер принимает решение, что на интервале от t1 до t10 по каналу передавалась последовательность кодовых символов, соответствующая выжившему пути  , т.е.: 11,10,00,10,11,00,11,01,10. Эта последовательность совпадает с
, т.е.: 11,10,00,10,11,00,11,01,10. Эта последовательность совпадает с  от момента t1 до t10 . Таким образом, ошибки возникшие на выходе демодулятора, оказываются исправленными.
от момента t1 до t10 . Таким образом, ошибки возникшие на выходе демодулятора, оказываются исправленными.
4. По выжившему пути, перенесенному на решетчатую диаграмму кодера, определить соответствие информационным символам k, которые поступали на вход сверточного кодера, принятых кодовых символов с учетом исправленной ошибки.
Согласно выжившему пути:

Последовательность информационных символов, поступивших на вход кодера:

Таким образом, можно убедиться, что ошибка, допущенная в 10 тактовом интервале была исправлена и на выходе декодера получилась та же комбинация, что и на выходе кодера.
ЛИТЕРАТУРА
1. Сальников А.П. Теория электрической связи: Конспект лекций СПбГУТ. – СПб., 2007. – 273 с.: ил.
2. Общая теория связи: методические указания к выполнению курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб. : Издательство СПбГУТ, 2012. – 80 с.
3. . Теория электрической связи:учеб.пособие для студ.высших учебных заведений /Р.Р.Биккенин, М.Н. Чесноков. - СПб.:Издательский центр «Академия» , 2010.-336с.
Дата добавления: 2018-02-15; просмотров: 1737; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
