Ортогональные представления сигналов
При анализе прохождения сложного сигнала s(t) через линейную систему (идеальная система, у которой зависимость Uвых от Uвх строго линейна) сигнал представляют в виде [5]
(2.3)
где jk(t) - базисные функции;
Ck - безразмерные коэффициенты.
Если базисные функции (базис) заданы, то s(t) полностью определяется коэффициентами Ck, совокупность которых называют обобщённым дискретным спектром сигналаs(t).
За пределами интервала [t1,t2] сигнал (2.3) считается условно продолжающимся, что может оказаться неприемлемым для представления сигналов конечной длительности.
Для представления ограниченного во времени сигнала применяется интеграл
, (2.4)
где j(a,t) - базисная функция непрерывного аргумента a;
S(a) - спектральная плотность, описывающая непрерывный, сплошной спектр.
Сравнивая выражения (2.3) и (2.4), можно отметить, что S(a)da - аналог безразмерного коэффициента Ck.
Совокупность методов представления в виде (2.3) и (2.4) называется обобщенной спектральной теорией сигналов.
Требования к базисным функциям.
1. Простое аналитическое выражение.
2. Быстрая сходимость ряда (2.3).
3. Простота вычисления коэффициентов Ck.
4. Простота технической реализции.
Этим требованиям отвечают ортогональные базисные функции, удовлетворяющие условию:
|
|
|
. (2.5)
При умножении всех функций ji(t), i= 
на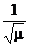 
, система функций ji(t) будетортонормированной (ортонормальной) и
. (2.6)
Вернемся к представлению (2.3) в случае ортогональности ji(t).
Умножим правую и левую от знака равенства части выражения (2.3) на jj(t) и проинтегрируем на отрезке [t1,t2], лежащем внутри интервала ортогональности [a,b].
или
.
При j¹k все интегралы в правой части этого выражения равны 0, а при j=k равны 1 (в соответствии с (2.6)). Следовательно,
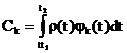. (2.7)
Важное свойство - сходимость ряда (2.3) к функции s(t). Для оценки этой сходимости используют различные критерии.
При среднеквадратической сходимости оценку осуществляют по критерию
. (2.8)
Примеры ортогональных систем
1. Система тригонометрических функций
ортонормированна на отрезке [-p,p], при переходе к 
имеет вид
|
|
|
(ортонормированна на отрезке 
).
2. Система показательных функций
; k=-¥,...,-2,-1,0,1,2,...,¥
также ортонормированна на отрезке [-p,p].
3. Полиномы Лежандра ортогональны на [-1,1]
j0(t)=1;
j1(t)=t;
j2(t)=  ;
j3(t)=  ;
 .
| 
Нормированные функции Лежандрa
 .
|
Полиномы Лежандра ортонормальны с весом e-t на интервале (0,¥),
| j0(t)=1; |
| j1(t)=-t+1; |
j2(t)=  ;
|
jn(t)=  .
|
4.Полиномы Чебышева ортогональны на интервале [1,-1] с весом 
.
j0(t)=  ;
j1(t)=  ;
j2(t)=  ;
j3(t)=  ;
jn(t)= 
| Полиномы Чебышева удовлетворяют условию наилучшей аппроксимации в среднеквадратической метрике на системе равноотстоящих точек. | ||
|
5.Полиномы Эрмита, ортонормированы на [-¥,¥] c весом
 Мы поможем в написании ваших работ! | |||
.