Оптимізація результатів за заданими критеріями
Міністерство транспорту та зв’язку України
Українська державна академія залізничного транспорту
Факультет “Управління процесами перевезень”
Кафедра “Управління експлуатаційною роботою”
Т.В.Бутько, О.М.Ходаківський, В.В.Петрушов, В.М.Прохоров
МЕТОДИ ДОСЛІДЖЕННЯ СИСТЕМ
Конспект лекцій для студентів денної і заочної форми навчання та слухачів ІППК з дисципліни
“Основи теорій систем і управління”
Частина 2
Харків 2009
Методи дослідження систем: конспект лекцій / Т.В.Бутько, О.М.Ходаківський, В.В.Петрушов, В.М.Прохоров. – Харків: УкрДАЗТ, 2009. – 32 с.
У конспекті лекцій наведено методи дослідження систем, процедуру оптимізації результатів за заданими критеріями, моделі систем на основі методів математичного програмування і т. ін., а також список контрольних питань і література.
Рецензент
проф. Д.В. Ломотько
Зміст
Вступ………………………………………………………………......4
1 Методи дослідження систем. Класифікація моделей...…………..5
2 Оптимізація результатів за заданими критеріями………………...6
3 Моделювання систем на основі методів математичного програмування ………... .……...…………………………………....12
4 Моделі систем на основі теорії масового
обслуговування………………..…………………………………….14
|
|
|
5 Методи прийняття рішень……………………………….………...14
6 Управління системою……………………………………………...19
7 Структура керуючої системи .....…………………………………..21
8 Проектування, конструювання та експлуатація систем.................35
9 Принципи формування систем ……………………………………36
Список контрольних питань ……………………………………...…37
Література ……………………………………………………………38
Вступ
Дисципліна «Основи теорій систем і управління» призначена для ознайомлення студентів з основними принципами функціонування складних систем та їх управління.
В другій частині лекційного курсу представлено методи дослідження складних систем та класифікація моделей. Наведено методи математичного дослідження систем, розглянуто критерії оптимізації результатів та методи прийняття рішень. Також розглянуто основні принципи управління системою, показники її функціонування та методологія проектування і конструювання систем. Наприкінці курсу викладено обґрунтування необхідності створення систем та принципи експлуатації технічних систем. Протягом вивчення курсу на лабораторних заняттях студенти повинні закріплювати матеріал, виконуючи розрахунки у програмному комплексі MathLab.
|
|
|
Друга частина лекційного курсу складається з 18 годин лекцій та 18 годин лабораторних занять.
Методи дослідження систем. Класифікація моделей
Основним методом дослідження системи є побудова її математичної моделі. Математична модель – це формалізоване подання системи у вигляді математичних символів або алгоритмів. Таким чином, дослідження системи зводиться до дослідження її математичної моделі. Математична модель дозволяє досліджувати систему з виключенням істотних або неістотних зв'язків; реалізовувати умови, недосяжні на практиці; прогнозувати стан системи.
Вибір методу дослідження математичної моделі безпосередньо пов'язаний з такими поняттями, як зовнішня та внутрішня правдоподібність.
Під зовнішньою правдоподібністю розуміється очікуваний ступінь адекватності математичної моделі реальному об'єкту.
Під внутрішньою правдоподібністю розуміється очікуваний ступінь точності рішення отриманих рівнянь, які прийняті у якості математичної моделі об'єкта.
Якщо тип моделі обраний, то зовнішню правдоподібність вважають зафіксованою, а вибір методу дослідження буде визначатися необхідним ступенем внутрішньої правдоподібності.
|
|
|
Складні та дуже складні стохастичні системи мають необхідність у керуванні. Якщо на систему здійснюється цілеспрямований вплив і система реагує на нього, то такі системи називають керованими. У кожній керованій системі виділяють дві підсистеми – керовану і керуючу. Таким чином, управління – це цільовий вплив керуючої системи на об'єкт функціонування (керовану систему), при якому керована система послідовно переходить із множини різних можливих станів у такий стан, при якому досягається необхідна мета, тобто це процес приведення заданого об'єкта до стану, що відповідає меті.
Класифікація моделей. Математичні моделі можна розділити на два великих класи: детерміновані та стохастичні. У детермінованих моделях всі параметри та вихідні дані вважаються визначеними. У стохастичних моделях параметри, вихідні дані або одне з них носять імовірнісний характер, тобто описуються законами розподілів.
Для дослідження транспортних систем використовують наступні типи моделей: моделі лінійного програмування, нелінійного програмування, теорії масового обслуговування, динаміки середніх, динамічного програмування, стохастичного програмування, прогнозування, на основі нечіткої логіки, імітаційні моделі та ін.
|
|
|
Математичні моделі динамічних систем можуть бути досить складними. Тому в процесі їхнього дослідження відносно невеликі складові можна відкинути; нелінійні залежності можна замінити лінійними, імовірнісні компоненти – детермінованими. Все це дозволяє швидко одержати приблизне рішення задачі, а це у свою чергу допомагає у виборі точності методу дослідження.
Вибір методу дослідження моделі визначається типом системи. Так, статичні системи, як правило, представляють алгебраїчними рівняннями або їхніми системами. У цьому випадку використовують метод Крамера і Гаусса, а для систем великої розмірності – метод ітерацій на ПЕОМ. Динамічні системи описують диференційними рівняннями, результатом рішення яких є функції. У відсутності аналітичних рішень диференційні рівняння вирішують методом Рунге–Кутта або чисельними методами на ПЕОМ. Для вивчення особливостей динамічної системи будують її фазовий портрет, що являє собою множину фазових траєкторій на фазовій площині. Фазова траєкторія – зображення одного з можливих рішень диференційних рівнянь.
При дослідженні стохастичних систем, у яких протікають імовірнісні процеси, доцільно використовувати метод Монте – Карло. За допомогою цього методу визначають оптимальне рішення на множині можливих варіантів при проектуванні систем. Метод Монте–Карло, або метод статистичного моделювання, заснований на використанні випадкових чисел, які моделюють імовірнісні процеси. Виконуючи моделювання багато разів, отримують статистичний матеріал. На підставі отриманих статистичних даних формують емпіричні залежності. Математичною основою методу є закон великих чисел: при великій кількості статистичних випробувань імовірність того, що середнє арифметичне значення випадкової величини прямує до її математичного очікування, дорівнює 1, тобто 
, де Х – випадкова величина, 
– математичне очікування Х, 
– мале число.
Розіграш значення випадкової величини Х із заданою функцією розподілу 
зводиться до наступної процедури: одержати число R, рівномірно розподілене в інтервалі від 0 до 1 (наприклад, використовуючи стандартну функцію RND), і у якості значення Х взяти: 
, 
– функція, зворотна по відношенню до 
.
На практиці при організації та експлуатації транспортних систем широке поширення одержала теорія масового обслуговування (ТМО).
Проведення математичного дослідження систем. Математичне дослідження – це експеримент над моделлю. У процесі експерименту на системі за допомогою моделі визначають динаміку вихідних змінних або розподілу імовірнісних значень параметрів, які характеризують систему.
Математичне дослідження передбачає: виявлення причинно- наслідкових відносин у досліджуваній системі; ідентифікацію параметрів моделі; визначення особливостей поведінки функцій, що описують систему (екстремуми, інтервали монотонності, опуклості); встановлення керованих і керуючих параметрів, оптимізацію рішень за заданими критеріями і ін.
Ідентифікація параметрів моделі – це процес одержання кількісної оцінки параметрів. Для цього використовуються експериментальні дані, які оброблюють методами математичної статистики, регресійно-кореляційного аналізу (метод найменших квадратів), методом експертної оцінки.
Якщо зв'язки між параметрами системи представлені поліномом n-го ступеня з коефіцієнтами 
: 
, то для оцінки параметрів 
зручно використовувати метод найменших квадратів:
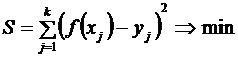. (1)
Оптимізація результатів за заданими критеріями
На етапах побудови моделі аналізу та інтерпретації отриманих результатів моделювання виконують оптимізацію структури системи або її окремих характеристик. Оптимізація – це процес пошуку і вибір одного рішення з множини можливих за заданим критерієм.
Критерій – це ознака, що дозволяє класифікувати процеси та характеристики на погані та хороші з огляду на поставлену мету. Кількісне вираження ознаки називають показником. При використанні одного критерію відбувається безпосередня оптимізація: 
.
У цьому випадку 
називають цільовою функцією.
Прикладом оптимізації в багатомірному Евклідовому просторі є задача лінійного та цілочисельного програмування, для рішення яких використовують відповідно сімплекс-метод і метод Гоморі. Більш адекватно описують задачі оптимізації в транспортних системах моделями нелінійного програмування. Методами рішення таких моделей є: метод множників Лагранжа та чисельні методи (метод релаксації, градієнта, найшвидшого спуску або підйому). При управлінні динамічними процесами використовують метод динамічного програмування.
Для існування оптимального рішення система обмежень у моделі повинна бути сумісною.
У дослідженнях систем часто зустрічаються багатокритеріальні завдання.
Багатокритеріальні завдання зводяться до однокритеріальних формуванням суперкритерію. Для формування суперкритерію використовують адитивні або мультиплікативні функції.
Суперкритерій в адитивній формі представляє собою суму доданків однієї розмірності: 
, де 
– часткові критерії; – коефіцієнти.
Суперкритерій у мультиплікативній формі представляє собою добуток часткових критеріїв: 
.
Виходячи з наведених вище понять, можна зробити висновок, що оптимізація за заданим критерієм можлива лише у тому випадку, коли множини можливих рішень перетинаються. Це призводить до необхідності введення поняття області припустимих рішень. Область припустимих рішень (ОПР) – множина, яка є результатом перетину двох або більше множин, в яких знаходяться рішення даної задачі. Саме в ОПР знаходиться вирішення задачі оптимізації.
Для оптимізації процесів у системі при взаємодії з іншими системами часто використовують методи теорії ігор. Теорія ігор – це математична теорія конфліктів. Метою теорії ігор є розробка рекомендацій для розумного поводження гравців у конфліктній ситуації, тобто визначення оптимальної стратегії для кожного з них (наприклад стратегія поводження залізничного і автомобільного транспорту на транспортному ринку). Ігри бувають антагоністичними і компромісними. Оптимальною стратегією гравця називають таку стратегію, яка при багаторазовому повторенні гри забезпечує даному гравцеві максимально можливий середній виграш. Розрахунки у грі ведуть за принципом: сторона А одержує найкращий результат при найгірших діях сторони В.
Дата добавления: 2018-02-15; просмотров: 812; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!