Задачи 9 – 16 решаются по темам «Относительные величины», «Средние величины», «Показатели вариации», «Выборочное наблюдение»
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Хабаровская государственная академия экономики и права» Кафедра статистики Общая теория статистики Задания к контрольной работе и методические указания по ее выполнению для студентов всех специальностей заочной формы обучения Хабаровск 2007 ББК У 051 Х 12 Общая теория статистики : задания к контрольной работе и методические указания по ее выполнению для студентов всех специальностей заочной формы обучения / сост. С. В. Февралева, И. В. Шокина. – Хабаровск : РИЦ ХГАЭП, 2007. – 36 c. Рецензент : В. В. Кузьминова, начальник отдела сводной информации Хабаровскстата Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов © Хабаровская государственная академия экономики и права, 2007 Указания к выполнению контрольной работы Выполнение письменной контрольной работы является обязательным этапом в изучении данного предмета студентами-заочниками. Цель контрольной работы – глубокое изучение важнейших методологических вопросов, проверка умений студента применять практические навыки в расчетах статистических показателей. Студент выполняет контрольную работу, вариант которой определяется в зависимости от начальной буквы фамилии студента и учебного года (таблица 1). Работа должна быть выполнена при соблюдении следующих требований: - необходимо указывать номер выполняемого варианта; - самовольная замена варианта или отдельной задачи не разрешается; - работа должна быть выполнена в сроки, установленные учебным планом; - задачи выполняются в последовательности, указанной в задании; - условие задания должно быть полностью приведено в работе; - решение должно сопровождаться формулами, подробными решениями, выводами, раскрывающими экономическое содержание и значение исчисленных показателей; - расчеты производятся в соответствии с принятой в статистике точностью до 0,001, а проценты – до 0,1; - работа должна быть оформлена аккуратно, написана разборчиво ручкой. Карандаш не допускается; - при компьютерном наборе формулы должны быть написаны в Microsoft Equation; - в работе должны быть поля, список использованных источников, оформленный в соответствии с библиотечными ГОСТами, дата выполнения работы; - выполненная работа сдается на проверку на кафедру через деканат. Работа, выполненная в соответствии с изложенными требованиями, допускается к защите, которая проводится во время сессии. В противном случае возвращается студенту через деканат на доработку; - исправленная работа вместе с первым (проверенным) экземпляром повторно сдается для проверки на кафедру через деканат; - при выполнении контрольной работы допускаются письменные консультации с четким изложением трудностей по адресу: 680042, г. Хабаровск, ул. Тихоокеанская, 134, Хабаровская государственная академия экономики и права, кафедра статистики, тел. 22-48-84. Таблица 1 – Ключ к определению варианта задания № вари-анта Начальная буква фамилии студента Номера выполняемых задач по учебным годам 2007– 2008 2008–2009 2009–2010 2010–2011 2011–2012 1 А,И,С,Щ 1,9,17,25, 33,41,49 4,12,20, 28,36,44, 52 2,10,18, 26,34,42, 50 3,11,19, 27,35,43, 51 5,13,21, 29,37,45, 53 2 Б,К,Т,Э 2,10,18, 26,34,42, 50 6,14,22, 30,38,46, 54 5,13,21, 29,37,45, 53 1,9,17,25,33,41,49 4,12,20, 28,36,44, 52 3 В,Л,У,Ю 3,11,19, 27,35,43,51 7,15,23, 31,39,47, 55 6,14,22, 30,38,46, 54 8,16,24, 32,40,48, 56 6,14,22, 30,38,46, 54 4 Г,М,Ф,Я 4,12,20, 28,36,44,52 1,9,17,25,33,41,49 7,15,23, 31,39,47,55 6,14,22, 30,38,46,54 8,16,24, 32,40,48,56 5 Д,Н,Х 5,13,21, 29,37,45,53 8,16,24, 32,40,48, 56 8,16,24, 32,40,48,56 2,10,18, 26,34,42,50 7,15,23, 31,39,47,55 6 Е,Ё,О,Ц 6,14,22, 30,38,46,54 3,11,19, 27,35,43,51 1,9,17,25,33,41,49 7,15,23, 31,39,47,55 2,10,18, 26,34,42,50 7 Ж,П,Ч 7,15,23, 31,39,47,55 2,10,18, 26,34,42,50 4,12,20, 28,36,44,52 5,13,21, 29,37,45,53 3,11,19, 27,35,43,51 8 З,Р,Ш 8,16,24, 32,40,48,56 5,13,21, 29,37,45,53 3,11,19, 27,35,43,51 4,12,20, 28,36,44,52 1,9,17, 25,33,41,49
|
|
|
|
|
|
Методические указания по выполнению контрольной работы
|
|
|
Задачи 1 – 8 решаются по теме «Средние величины»
Вид и форма средней выбирается исходя из экономического содержания исчисленного показателя. Cредняя арифметическая используется в том случае, когда в условии задачи даны значения осредняемого признака х и его частоты f:
 ,
,
где х – признак (варианта) – индивидуальные значения осредняемого признака;
f – частота, т.е. числа, показывающие, сколько раз повторяется та или иная варианта. В качестве частот можно использовать частости (частоты, выраженные в процентах).
Cредняя гармоническая взвешенная используется в том случае, когда даны значение осредняемого признака х и показатель  , представляющий собой реально существующий экономический показатель равный х∙ f:
, представляющий собой реально существующий экономический показатель равный х∙ f:
 ,
,
где х –признак (варианта) – индивидуальные значения осредняемого признака;
|
|
|
 - х∙ f
- х∙ f
Задачи 9 – 16 решаются по темам «Относительные величины», «Средние величины», «Показатели вариации», «Выборочное наблюдение»
Каждая задача состоит из 10 заданий.
Задание 1. Относительные величины структуры (структура) характеризуют состав изучаемой совокупности и показывают, какой удельный вес (какую долю) в общем итоге составляет каждая ее часть. Они получаются в результате деления каждой части совокупности на их общий итог, принятый за базу сравнения. Сумма относительных величин структуры изучаемой совокупности всегда равна 100%, или 1.
Задание 2. Мода и медиана являются структурными (распределительными) средними.
Мода – это наиболее часто встречающееся значение ряда:
 ,
,
где  – мода
– мода
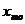 – нижняя граница модального интервала. Интервал с максимальной частотой является модальным;
– нижняя граница модального интервала. Интервал с максимальной частотой является модальным;
 – шаг модального интервала, который определяется разницей его границ;
– шаг модального интервала, который определяется разницей его границ;
fmo – частота модального интервала;
fmo-1 – частота интервала, предшествующего модальному;
fmo+1 – частота интервала, последующего за модальным.
Медианой является значение признака х, которое больше или равно и одновременно меньше или равно половине остальных элементов ряда распределения. Медиана делит ряд на две равные части:
 ,
,
где xme – нижняя граница медианного интервала. Интервал, в котором находится порядковый номер медианы, является медианным. Для его определения необходимо подсчитать величину  . Интервал с накопленной частотой равной величине
. Интервал с накопленной частотой равной величине  является медианным.
является медианным.
i –шаг медианного интервала, который определяется разницей его границ;
 – сумма частот вариационного ряда;
– сумма частот вариационного ряда;
Sme-1  – сумма накопленных частот в домедианном интервале;
– сумма накопленных частот в домедианном интервале;
fme – частота медианного интервала.
Задание 3. Средняя величина по ряду распределения определяется по формуле средней арифметической взвешенной:
 ,
,
где х –признак (варианта) – индивидуальные значения осредняемого признака, в качестве которого берется середина интервала, определяемая как полусумма его границ;
f – частота, т.е. числа, показывающие, сколько раз повторяется та или иная варианта.
Задание 4 – 8 по теме «Показатели вариации».
Размах вариации:
 ,
,
где хmax – максимальное значение признака;
х min – минимальное значение признака;
- среднее линейное отклонение:
 ,
,
где  – индивидуальные значения признака,
– индивидуальные значения признака,
 – средняя величина;
– средняя величина;
f – частота;
- дисперсия:
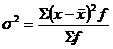 ;
;
- среднее квадратическое отклонение:
 ;
;
- коэффициент вариации:
 .
.
Коэффициент вариации показывает степень однородности совокупности. Если V < 33% – совокупность однородна.
Задание 9 – 10 по теме «Выборочное наблюдение».
Суть выборочного наблюдения заключается в том, что из генеральной совокупности в случайном порядке отбирается часть единиц (выборочная совокупность) и по данным выборки рассчитываются обобщенные характеристики (средние или относительные показатели – доля единиц, обладающих данным признаком), а затем результаты распространяются на всю генеральную совокупность.
Границы генеральной средней (задание 9):
 ,
,
где  – генеральная средняя,
– генеральная средняя,
 – выборочная средняя,
– выборочная средняя,
Δ  – предельная ошибка выборочной средней:
– предельная ошибка выборочной средней:
 ,
,
где  – коэффициент доверия, зависящий от вероятности исследования: при вероятности 0,954 t = 2, а при вероятности 0,997 t = 3;
– коэффициент доверия, зависящий от вероятности исследования: при вероятности 0,954 t = 2, а при вероятности 0,997 t = 3;
n – объем выборочной совокупности;
N – объем генеральной совокупности;
 – доля отбора единиц из генеральной совокупности в выборочную;
– доля отбора единиц из генеральной совокупности в выборочную;
 – дисперсия признака выборочной совокупности, методика определения и величина которой представлена в задании 6.
– дисперсия признака выборочной совокупности, методика определения и величина которой представлена в задании 6.
Границы генеральной доли (задание 10):
 ,
,
где р – генеральная доля,
 – выборочная доля:
– выборочная доля:
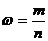 ,
,
где  – число единиц, обладающих данным или изучаемым признаком;
– число единиц, обладающих данным или изучаемым признаком;
n – объем выборочной совокупности;
 – предельная ошибка доли:
– предельная ошибка доли:
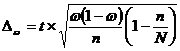 ,
,
где n – объем выборочной совокупности;
N – объем генеральной совокупности;
 – доля отбора единиц из генеральной совокупности в выборочную.
– доля отбора единиц из генеральной совокупности в выборочную.
Дата добавления: 2018-02-15; просмотров: 72; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
