Тема № 3. «Теоретические основы теплоэнергетики»
Пример 1-1. За τ = 20 ч работы электростанции сожжено
В = 62 т каменного угля, имеющего теплоту сгорания
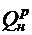= 28900 кДж/кг.
Определить среднюю мощность станции, если в электрическую энергию превращено 20 % теплоты, полученной от сгорания топлива.
Решение:
Количество теплоты, превращенной в электрическую энергию 
= 62 · 103 · 28,9 · 103 · 0,2 = 354,6 · 106 кДж.
Эквивалентная ему электроэнергия или работа
кВт·ч.
Средняя электрическая мощность станции
кВт.
Пример 1-2. Один кг воздуха совершает цикл Карно в пределах температур от Т1 = 900 К до Т2 = 300 К. Наивысшее давление в цикле – 6 МПа, а наинизшее – 0,1 МПа. Определить термический КПД цикла.
Решение:
Цикл Карно состоит из изотермических процессов 1-2 и 3-4 подвода теплоты q1 и отвода теплоты q2 и адиабатных процессов расширения (2-3) и сжатия (3-4) без теплообмена (q1 = 0).
Точка 1: р1 = 6 МПа, Т1 = 900 К (по заданию). Удельный объем воздуха находим из уравнения состояния:
м3/кг.
Точка 2: Т2 = 900 К. Из уравнения адиабаты (к = 1,4)
МПа.
Удельный объем воздуха
м3/кг.
Точка 3: р3 = 0,1 МПа, Т3 = 300 К (по заданию)
м3/кг.
Точка 4: Т4 = 300 К
МПа.
Из уравнения изотермы 3-4 
м3/кг.
Термический КПД цикла 
.
Количество подведенной теплоты 
кДж/кг.
Количество отведенной теплоты 
кДж/кг.
Работа цикла lц = q1 – q2 = 42,5 кДж/кг.
Проверка: 
Пример 1-3. Для условий предыдущей задачи определить, как изменятся параметры в основных точках цикла, термический КПД, теплота и работа, если в качестве рабочего тела использовать кислород или азот.
|
|
|
В результате решения задачи Вы должны убедиться, что замена одного рабочего тела на другое (воздуха на О2 или N2) приводит к изменению параметров в характерных точках цикла и количествах подведенной и отведенной теплоты. Термический КПД цикла не зависит от свойств рабочего тела.
Пример 1-4. Определить параметры сухого насыщенного пара при давлении 5 МПа.
Решение:
В h-s диаграмме (приложение 1) на пересечении линий х = 1 и изобары 5 МПа (50 бар) находим точку 1, которая определяет состояние пара. По изохоре и изотерме, проходящим через точку 1, находим соответственно 
м3/кг и t1 = 264 оС, энтальпия 
кДж/кг, энтропия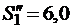 
кДж/(кг·К). Эти же параметры можно найти из таблиц термодинамических свойств воды и водяного пара.
Пример 5. Определить параметры влажного пара при давлении 5 МПа и степени сухости х = 0,94.
Решение:
Состояние влажного пара с заданными параметрами в h-s диаграмме определяет точка 1, которая находится на пересечении изобары 5 кПа (0,05 бара) и линии постоянной степени сухости
х = 0,94. Проектируя на ось абсцисс и ось ординат находим: энтальпия h1х = 2416 кДж/кг и энтропия S1х = 8 кДж/(кг·К). Величилина удельного объема определяется по значению изохоры, проходящей через точку 1 – v1х = 25,4 м3/кг. В точке пересечения изобары 5 кПа и линии х = 1 находится температура насыщенного пара t1х = 33 оС.
|
|
|
Те же параметры можно найти с помощью таблиц и формул:
h1х = h' + хч = 137,8 + 2423 · 0,94 = 2416 кДж/кг;
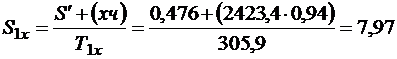кДж/кг·К;
v1х = v''х = 28,2 · 0,94 = 26,5 м3/кг.
Из таблицы воды и водяного пара по давлению р = 5 кПа берут значения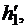 
τ1, 
v''.
Совпадение параметров удовлетворительное.
Пример 6. Определить параметры перегретого водяного пара при давлении 10 МПа и температуре 500 оС.
Решение:
В h-s диаграмме находим точку 1, характеризующую состояние пара, на пересечении изобары 10 МПа и изотермы
500 оС. Проектируя точку 1 на координатные оси, получим h1 = 3374 кДж/кг и S1 = 6,6 кДж/кг·К. По значению изохоры, проходящей через точку 1, – v1 = 0,033 м3/кг. Изотерма, проходящая через точку пересечения изобары 10 МПа и линии х = 1, определяет температуру насыщенного пара tн = 311 оС. Искомые параметры можно найти по таблицам перегретого пара при давлении 10 МПа и температуре 500 оС.
Пример 7.Плоская стальная стенка толщиной 
мм омывается с одной стороны газами с температурой 
= 310 оС, а с другой изолирована от окружающего воздуха, имеющего температуру 
= 10 оС, плотно прилегающей к ней пластиной толщиной 
мм.
|
|
|
Определить плотность теплового потока и температуры поверхностей стенок, если известно, что коэффициент теплопроводности стали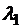 
= 40 Вт/(м·К), а материала изоляционной пластины 
= 0,15 Вт/(м·К). Коэффициент теплоотдачи от газов к стенке 
= 25 Вт/(м2·К), а от пластины к воздуху 
=
= 10 Вт/(м2·К).
Решение:
Полное термическое сопротивление плоской многослойной стенки 
(м2·К)/Вт.
Коэффициент теплопередачи k = 
Вт/(м2·К).
По уравнению теплопередачи плотность теплового потока q: 
, Вт/м2.
Температура 
на поверхности стальной стенки 
,
на границе между стальной стенкой и изоляционной пластиной 
, на поверхности изоляционной пластины 
.
Пример 8.Через трубу диаметром d = 50 мм и длиной l = 3 м со скоростью w = 0,8 м/с протекает вода. Определить средний коэффициент теплоотдачи, если средняя температура воды 
= 50 оС, а температура стенки 
= 70 оС.
Решение:
При = 50 оС,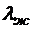 
= 0,648 Вт/(м·К), 
= 5,56·10-7 м2/с, 
= 3,54, 
= 2,55 при = 70 оС (табл. П. 11 приложения).
Определим режим течения воды: 
, режим турбулентный. В этом случае критериальное уравнение имеет вид:
|
|
|
,
,
, Вт/(м2·К).
Так как 
= 60 > 50, то поправка на влияние длины трубы
= 1.
Пример 9. Определить, какое количество сухого насыщенного пара давлением 0,198 МПа, сконденсируется в стальном горизонтальном трубопроводе диаметром d = 140 мм на длине
= 12 м, если он находится в кирпичном канале a·b = 0,5·0,5 м, температура стенок канала 
= 20 оС. Коэффициент теплоотдачи при естественной конвенции в канале 
= 12 Вт/(м2·К).
Решение:
Температура пара 
= f(р), = 120 оС; считать температуру стенки паропровода равной , 
.
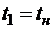Боковые поверхности трубы и канала F1 =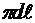 
; F2 = 2(a+b) · , м2.
Коэффициент лучистого теплообмена 
л
, Вт/(м2·К),
где 
пр – приведенная степень черноты системы, Сo = 5,7 Вт/(м2·К4); 
, 
= 0,7, 
= 0,82.
Суммарный коэффициент теплоотдачи от стального паропровода к воздуху в канале 
, Вт/(м2ּК).
Потери теплоты в паропроводе 
, Вт.
Количество конденсируемого пара D= 
, кг/ч, где r, 
–скрытая теплота парообразования, выбирают по давлению р из табл. П. 5 приложения.
Пример 10. В теплообменнике 
= 2 кг/с воды нагреваются от температуры 
до 
С горячими газами, которые при этом охлаждаются от температуры 
С до температуры 
С.
Определить поверхность теплообменника при включении его по схеме прямотока и противотока, если коэффициент теплопередачи k = 32 Вт/( 
).
Решение:
Количество теплоты, полученное водой от газов, найдем по уравнению теплового баланса: 
, Вт.
Среднелогарифмический температурный напор:
для прямотока 
;
для противотока 
.
Из уравнения теплопередачи поверхность теплообменника 
; 
.
Пример 11. Для паровой турбины мощностью 
кВт с удельным расходом пара 
= 5,5 кг/(кВт·ч) определить поверхность охлаждения конденсатора и расход охлаждающей воды, если известно, что кратность охлаждения m = 55 кг/кг и температура охлаждающей воды на входе в конденсатор 
оС, на выходе 
оС. Температура пара в конденсаторе 
оС. Коэффициент теплопередачи k = 3700 Вт/(м2·К).
Решение:
Расход пара турбиной D =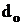 
N, т/ч. Расход охлаждающей воды W = Dm, т/ч. Отводимая в конденсаторе теплота 
, Дж/ч. Температурный напор в конденсаторе 
.
Поверхность охлаждения конденсатора 
, м2.
Дата добавления: 2018-02-15; просмотров: 1837; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!