Распространение выборочных результатов на генеральную совокупность и определение необходимого объема выборки
Главной задачей выборочного наблюдения является характеристика генеральной совокупности на основе полученных выборочных показателей, т.е. распространение выборочных результатов на генеральную совокупность.
Значение выборочной средней распространяют на генеральную среднюю с учётом предельной ошибки. В этом случае предельные значения генеральной средней равны:
,
а границы доверительного интервала генеральной средней определяются следующим образом:
.
Таким образом, можно утверждать, что с заданной вероятностью значение генеральной средней будет находиться в пределах от 
до 
.
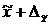Очевидно, что увеличивая объем выборки, можно уменьшить значения средней и предельной ошибок выборочного наблюдения и, следовательно, сузить границы доверительного интервала генеральной средней. Однако большой объем выборки приводит к увеличению сроков сбора и обработки информации, стоимости обследования, расхода материальных ресурсов, привлечению дополнительных кадров. Как показывает практика затраты всех ресурсов на 20-30%-ное выборочное наблюдение могут быть сопоставимы с расходами на сплошное обследование. Однако выборочные показатели всегда полностью не характеризуют генеральную совокупность и, поэтому, будут уступать результатам сплошного наблюдения по точности и надежности. Таким образом, важным вопросом подготовки выборочного наблюдения является необходимость определения минимально допустимого объема выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.
|
|
|
Расчет необходимого объема выборки предполагает, что организаторы выборочного наблюдения уже на этапе его проектирования располагают по крайней мере косвенными данными о вариации изучаемых признаков. Источниками таких данных могут служить:
а) результаты исследования данного объекта в предшествующие периоды;
б) результаты исследования аналогичных объектов (жителей других населенных пунктов, предприятий других регионов и т.п.);
в) специально проведенное небольшое по объему выборочное обследование данного объекта, ставящее целью лишь изучение вариации наблюдаемых признаков.
Формулу расчёта объема выборки можно получить из соответствующей формулы предельной ошибки.
Для случайнойвыборки необходимый объём определяется следующим образом:
(для повторного отбора)
(для бесповторного отбора)
Необходимый объём выборки в условиях механического отбора определяется аналогично объёму случайной бесповторной выборки.
При определении необходимого объематипической выборкив рассмотренных выше формулах общую дисперсию наблюдаемого признака заменяют на среднюю из внутригрупповых дисперсий.
|
|
|
(для условий повторного отбора)
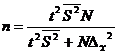(для бесповторного отбора)
Объём серийной (групповой) выборки определяется с учётом межгрупповой дисперсии:
(для повторного отбора)
(для бесповторного отбора)
Как следует из рассмотренных выше формул необходимого объёма выборки, при увеличении предполагаемой предельной ошибки необходимый объём выборки значительно уменьшается.
Кроме того, следует иметь в виду, что вместо генеральной дисперсии определенного вида может использоваться значение, полученное из ранее проводимых обследований данной или аналогичной совокупности. Если такая информация отсутствует, то для определения дисперсии необходимо организовать и провести специальное выборочное обследование небольшого объёма.
Контрольные вопросы:
1. Дайте определение выборочного наблюдения и охарактеризуйте его задачи.
2. Какие этапы включает в себя проведение выборочного наблюдения?
3. Назовите основные виды, методы и способы отбора.
4. Раскройте сущность ошибок выборочного наблюдения?
5. Каким образом определяют среднюю и предельную ошибки наблюдения для разных видов выборки?
|
|
|
6. Каким образом распространяют выборочные данные на генеральную совокупность?
7. Как определяется необходимая численность выборки?
Тесты:
1. По формуле 
определяется ________ ошибка при ___________ отборе.
a) средняя, бесповторном
б предельная, бесповторном
в) средняя, повторном
г) предельная, повторном
2. Для использования выборочной совокупности для дальнейшего анализа развития социально-экономического явления необходимо, чтобы разница между средним значением генеральной совокупности и средним значением выборочной совокупности была не больше __________ ошибки выборки.
a) предельной
б) средней
в) генеральной
г) индивидуальной
3. Выборка, заключающаяся в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора, называется…
a) механической
б) типической
в) случайной повторной
г) случайной бесповторной
4. При случайном бесповторном отборе средняя ошибка выборки определяется по следующей формуле…
a) 
б) 
в) 
г)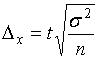 
5. Если при переписи населения 25 % населения отвечало на дополнительные вопросы переписного листа и в выборку попало каждое четвертое жилое помещение, то использовался ___________ способ формирования выборочной совокупности.
a) механический
б) случайный
в) типический
г) серийный
|
|
|
6. По формуле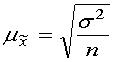 
определяется __________ ошибка выборки.
a) средняя
б) предельная
в) генеральная
г) индивидуальная
7. Выборка называется малой в том случае, если ее объем составляет менее ___ единиц.
a) 30
б) 50
в) 100
г) 40
8. Если сплошному обследованию подвергаются случайно отобранные группы единиц, то выборка называется …
a) серийной
б) механической
в) типической
г) случайной
9. Для получения предельной ошибки выборки необходимо _________ умножить на среднюю ошибку выборки
a) t
б) p
в) n
г) N
10. При случайном повторном отборе средняя ошибка выборки определяется по формуле …
a)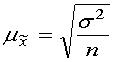
б)
в)
г)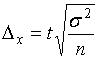
Дата добавления: 2018-02-15; просмотров: 946; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!