Свойства функции распределения
1. 
, 
.
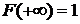2.Значения функции распределения принадлежат отрезку [0,1]:
.
3. 
– неубывающая функция, т.е. если 
> 
, то 
> 
.
4. Вероятность того, что случайная величина примет значение в интервале 
равна 
:
< 
< 
.
Наряду с функцией распределения для задания случайной величины используют также функцию, которая называется плотностью распределения.
Определение.Плотностью распределения вероятностей непрерывной случайной величины называется такая неотрицательная функция 
, определенная на всей числовой оси, что для всех 
:
.
Из этого определения следует, что, зная плотность распределения , можно найти функцию распределения 
. И наоборот, по известной функции распределения можно восстановить плотность распределения:
.
Приведем примеры наиболее известных и применяемых распределений случайных величин.
1. Равномерно распределенная случайная величина
Определение.Случайная величина называется равномерно распределенной на отрезке 
, если ее плотность распределения вероятностей имеет вид: 
Рис.3 
График плотности распределения вероятностей равномерно распределенной случайной величины приведен на рисунке ?
Математическое ожидание такой случайной величины вычисляется по формуле 
, а дисперсия – по формуле 
.
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений.
|
|
|
Задача 3.Поезда метрополитена идут регулярнос интервалом 2 мин. Пассажир приходит на станцию в случайный момент времени. Найдите вероятность того, что ждать поезда пассажиру придется не больше полминуты. Найдите также математическое ожидание и среднее квадратическое отклонение времени ожидания поезда.
Решение. Случайная величина –время ожидания поезда на временном интервале [0,2] (в минутах) имеет равномерный закон распределения 
(см. рис.3). Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 
от равной 1 площади прямоугольника, т.е. 
.
, 
, 
.
2. Показательное распределение случайной величины
Определение.Случайная величина называется распределенной по показательному закону, если ее плотность распределения имеет вид:
График плотности распределения этой случайной величины приведен на рисунке 4.
Рис.4
Для случайной величины, распределенной по этому закону, основные характеристики вычисляются по формулам:
|
|
|
, 
, 
.
3. Случайная величина, распределенная по нормальному закону
Определение.Случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:
,
где 
и 
– параметры нормального распределения: параметр является математическим ожиданием случайной величины, а параметр – ее средним квадратическим отклонением. График этой функции представлен на рисунке 5.
Рис.5
Нормальное распределение называют также Гауссовским. Это – наиболее часто встречающийся на практике закон распределения вероятностей. О значении этого закона говорит следующая теорема, которая носит название центральной предельной теоремы:
Если случайная величина представляет собой сумму очень большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.
На всех рисунках площадь заштрихованной фигуры равна вероятности попадания значений рассматриваемой случайной величины на указанный отрезок 
.
3.4.4.Задачи для самостоятельного решения
|
|
|
4. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Составить ряд распределения числа отказавших элементов в одном опыте.
5. Охотник дважды стреляет по цели. Вероятность попадания стрелка при одном выстреле равна 0, 7. Составить ряд распределения числа попаданий стрелка в цель и построить многоугольник полученного распределения.
6. Два стрелка независимо друг от друга производят по одному выстрелу по цели. Вероятность попадания в цель первого стрелка равна 0,8, а второго – 0,7. Составьте ряд распределения числа попаданий в цель.
7. Найдите математическое ожидание и дисперсию случайной величины:
| Х | 0 | 2 | 3 |
| Р | 0,3 | 0,5 |
8. Найдите математическое ожидание и дисперсию случайной величины:
| Х | 0 | 2 | 3 |
| Р | 0,4 | 0,3 |
9. Найдите математическое ожидание и дисперсию случайных величин из задач 3 – 5.
. 10. Дискретная случайная величина задана рядом распределения:
| Х | 1 | 3 | 4 | 6 |
| Р | 0,2 | 0,3 | 0,2 | 0,3 |
|
|
|
Найдите функцию распределения и постройте ее график.
11. Дана функция распределения непрерывной случайной величины :
Найдите плотность распределения и постройте ее график.
12. Случайная величина равномерно распределена на отрезке
[-2,3]. Запишите выражение для функции распределения этой случайной величины.
13. Время горения красного сигнала светофора 20 сек. Автомобиль остановился на перекрестке на красный свет. Найдите вероятность того, что он уедет с перекрестка позднее, чем через 15 секунд. 0,25
14. Рейсовый автобус движется по маршруту строго по расписанию с интервалом 10 мин. Найдите вероятность того, что случайно подошедший к остановке пассажир будет ожидать автобуса менее 2 минут. 0,2
15. Рейсовый автобус движется по маршруту строго по расписанию с интервалом 12 мин. Найдите вероятность того, что случайно подошедший к остановке пассажир будет ожидать автобуса менее 3 минут. Найдите также математическое ожидание, дисперсию и среднее квадратическое отклонение времени ожидания автобуса. 6 мин., 12 мин 
, 2 
мин.
Дата добавления: 2018-02-15; просмотров: 570; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!