Вторые производные и производные более высоких порядков.
Глава 4.
Занятие 1.
Дифференцирование. Основные определения и правила.
Определение 1. 1. Пусть функция 
определена в открытом интервале 
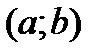и пусть точка 
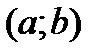принадлежит . Производной функции 
в точке назовем величину
(1.1)
Если предельное значение (1.1) существует и конечно.
Секущая и касательная прямые к графику функции 
.
Определение 1.2.
Секущей прямой к графику функции назовём прямую, проходящую через две точки лежащие на графике: 
. Уравнение этой прямой имеет вид: 
. Угловой коэффициент секущей 
равен 
рис.1
Если теперь точку 
неограниченно приближать вдоль графика к точке 
, то наклон секущей будет меняться. Допустим, что существует предельное значение 
углового коэффициента (при условии 
), то есть
(1.2)
Определение 1.3. Прямая 
называется касательной прямой к графику функции с точкой касания .
|
|
|
Сравнивая формулы (1.1) и (1.2) получаем алгоритм вычисления касательной прямой к графику функции 
в точке 
.
1 шаг.Вычисляем производную функции 
.
2шаг. Выписываем уравнение касательной прямой в точке касания
(1.3)
Если 
, то касательная параллельна оси ОХ и её уравнение будет таким 
.
Пример 1.1. На графике функции 
заданы две точки 
. Написать уравнения прямых:
1) Секущей прямой проходящей через точки А и В;
2) Уравнения касательных прямых к графику проведённых
в точках А и В.
Решение. 1) Определяем угловой коэффициент секущей прямой 
.
Выписываем уравнение секущей 
или 
. Чтобы написать уравнения
касательных нужно вычислить значения производных функции в точках касания: 
и 
. Подставляя данные в формулу (4.3) выписываем уравнения касательных
; 
С помощью касательных определяют углы между графиками функций в точке их пересечения.
Определение 1.4. Углом между графиками функций 
в точке их пересечения называется угол между их касательными прямыми в этой точке рис. 2. Этот угол находим по формуле
|
|
|
Рис.2
(1.4)
Определение производной удобнее записывать и использовать с помощью приращений.
Разность 
обозначают через 
и называют приращением аргумента.
. Разность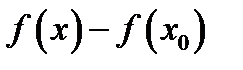 
= 
называют приращением функции. Таким образом, определение производной можно переписать так
(1.5)
Замечание. Производные можно записывать формулами 
Пример 1.2 . Найдём производные функций 
в точке 
.
Решение. Используя определение производной (1.5), вычисляем приращение функции в точке 
. Тогда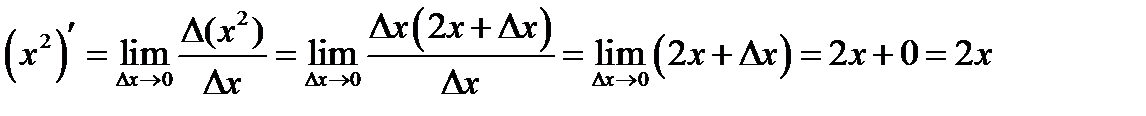 
.
Вычисляем производную функции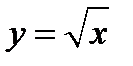 
.
По определению имеем 
Физический смысл производной.
Пусть координата точки движущейся вдоль прямой меняется со временем по закону 
Тогда средняя скорость за период времени 
определяется как 
Мгновенная скорость в момент времени 
есть (по определению) предельное значение средней скорости 
|
|
|
основные правила дифференцирования.
Для практического вычисления производных определения (1.1) и (1.5) малопригодны. Обычно поступают так: из определения производной получают правила дифференцирования и при вычислении любой производной пользуются этими правилами .
Правило 1.1.При дифференцировании постоянный сомножитель выносится за знак
производной: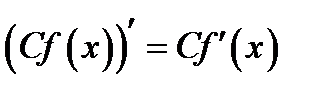 
Доказательство.
Правило 1.2. Производная суммы функций равна сумме производных 
. Доказательство.
Правило 1.3. Производная произведения двух функций равна производной первой функции, умноженной на вторую функцию плюс первая функция, умноженная на производную второй функции: 
Доказательство. 
Правило 1.4. Производная дроби равна произведению знаменателя на производную числителя минус произведение числителя на производную знаменателя, весь полученный результат делится на квадрат знаменателя: 
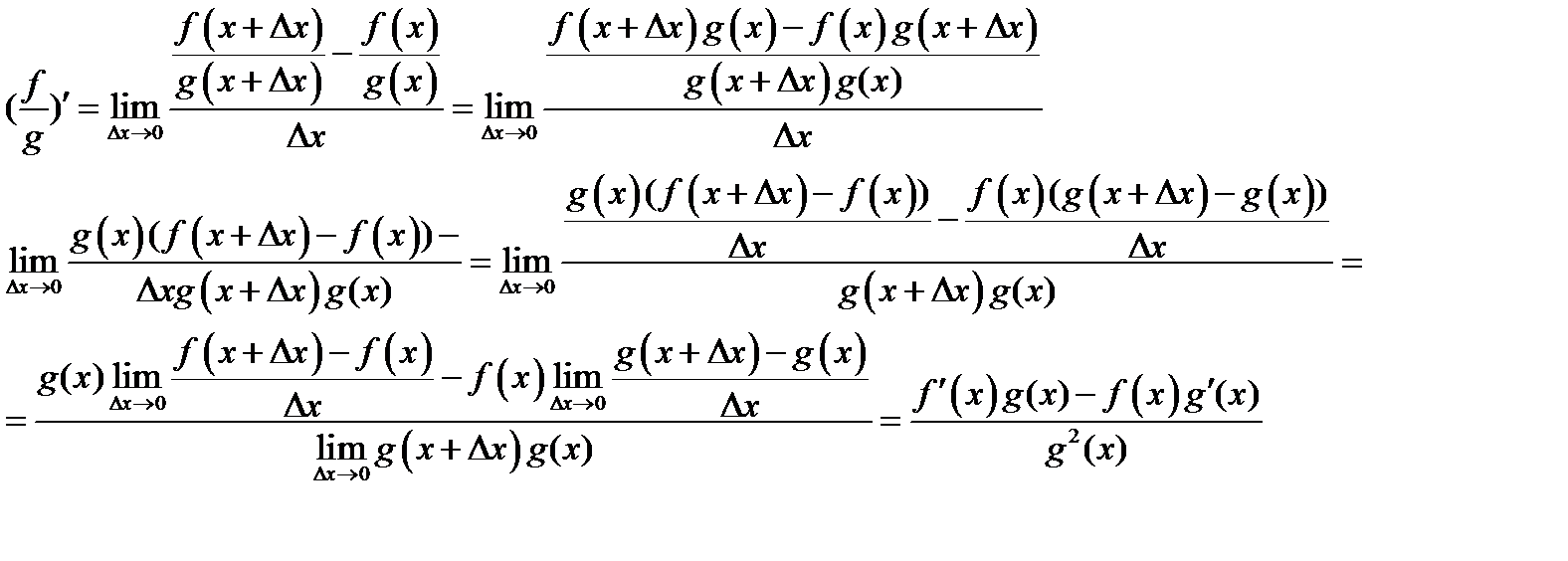
Получим таблицу производных всех базовых элементарных функций.
Для этого используем замечательные пределы. Приведем примеры.
1. производная тригонометрической функции 
|
|
|
2. производная тригонометрической функции 
3. производная показательной функции 
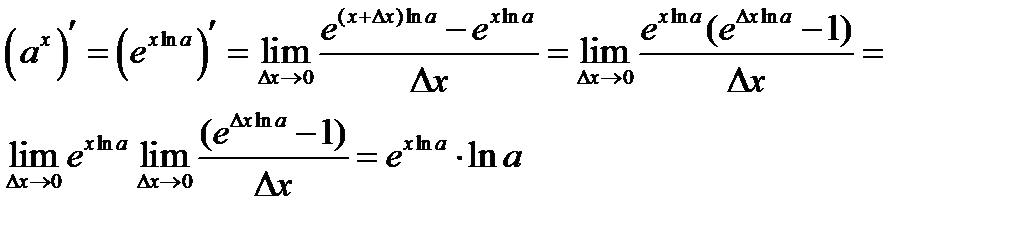
3. производная логарифмической функции 
1. 1. Таблица производных базовых элементарных функций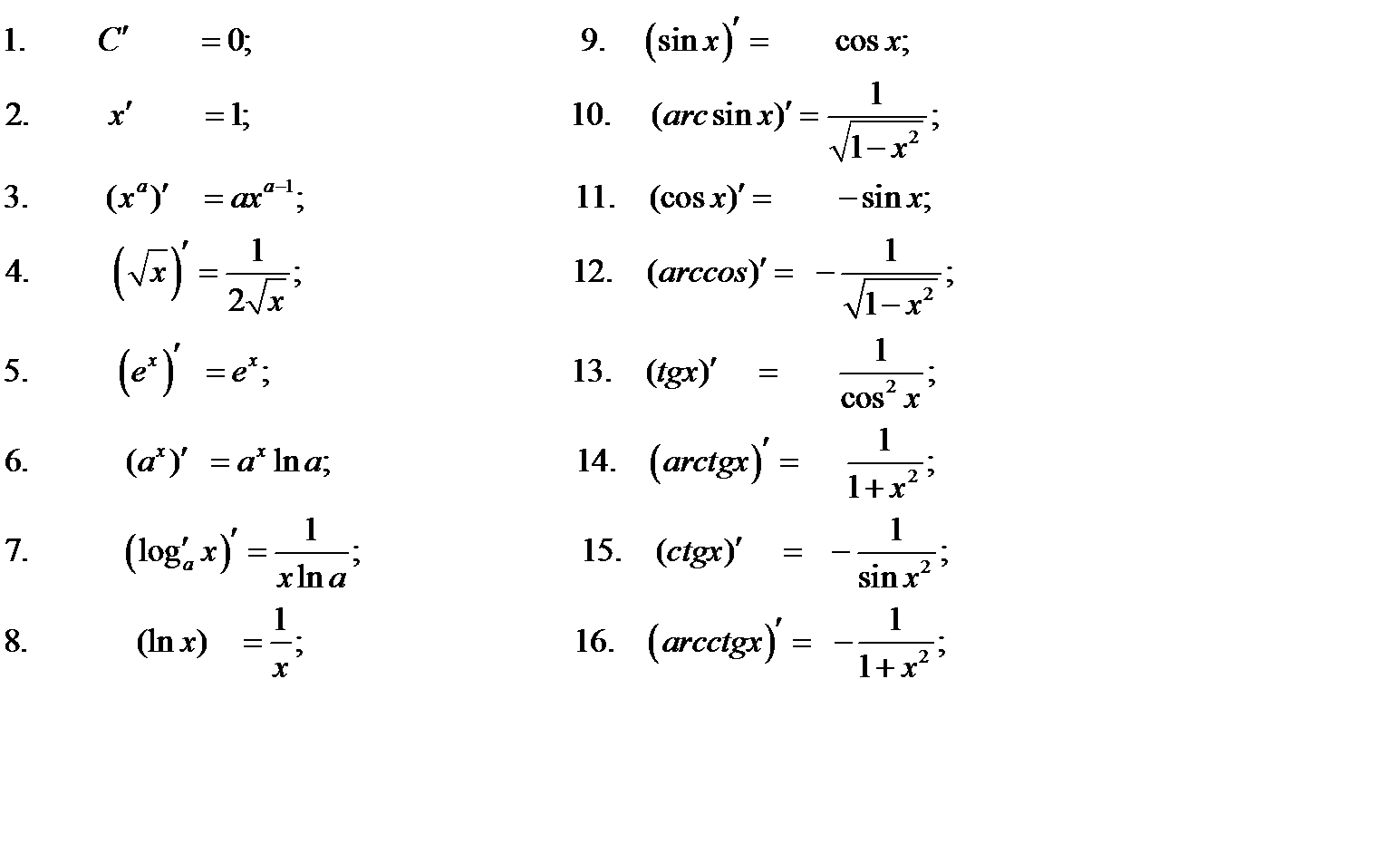 
Замечание. Вычисление производных произвольных функций несложно, но требует практических навыков.
Пример 1.3. Пользуясь правилом 1.3 вычислить производную функции 
.
Решение.
Упражнение 1.1. Используя правила дифференцирования и таблицу производных найти производные функций
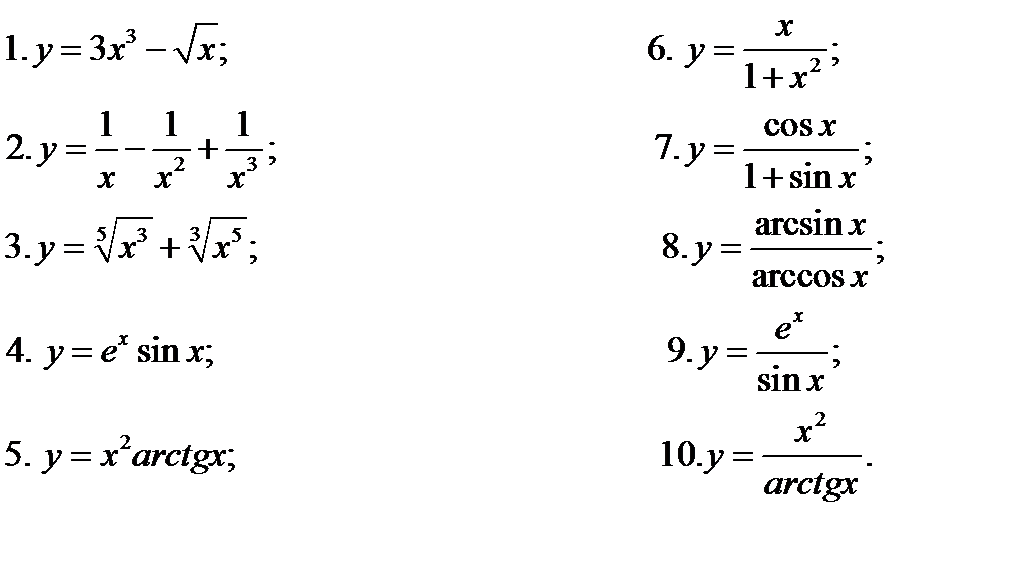
Вычислим производные функций заданные номерами 2, 5, 7,8,10. Остальные
производные заданных функций предлагаем найти самостоятельно.
Решение.
2. Переписываем функцию в удобном для дифференцирования виде 
. Следовательно 
5. 
7.
8.
10. 
Пример 1.4. Вычислить производную функции 
Решение. 
Далее все производные берём из таблицы производных и записываем ответ
.
Вторые производные и производные более высоких порядков.
Определение 1.5.Производная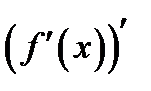 
от производной функции называется второй производной функции или производной второго порядка и обозначается формулой 
.
Замечание. Вторые производные можно записывать формулами 
.
Определение 1.6.Производная 
от второй производной функции называется третьей производной функции или производной третьего порядка и обозначается формулой 
.
Замечание. Вторые производные можно записывать формулами 
.
Замечание.Производные высших порядков определяются аналогично.
Пример 1.5.Вычислить производные второго, третьегои четвёртого порядков от функции 
.
Решение.
Замечание. При дифференцировании многочленов порядок его производной понижается при каждом дифференцировании на единицу и поэтому любой многочлен всегда имеет конечное число производных.
Пример 1.6.Вычислить все производные многочлена 
.
Решение. 
Дата добавления: 2018-02-15; просмотров: 1167; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!