ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДАТЧИКА ДАВЛЕНИЯ С ПОМОЩЬЮ ИНТЕРПОЛЯЦИИ КУБИЧЕСКИМИ СПЛАЙНАМИ

С.А. Кузин^*, Д.Н. Соколов^**, П.А. Львов^***, Д.А. Булыкин^****, Н.И. Мельникова^*****

^*Саратовский государственный технический университет имени Гагарина Ю.А.,
Саратов, Россия, sgen @ dimes . ru

^**Саратовский государственный технический университет имени Гагарина Ю.А.,
Саратов, Россия, sokolovdimajkr@gmail.com

^***Энгельсское опытно-конструкторское бюро «Сигнал» им. А.И. Глухарева,

Энгельс, Саратовская обл., Россия, peter . lvov @ gmail . com

^****Саратовский государственный технический университет имени Гагарина Ю.А.,
Саратов, Россия, d.bulykin@gmail.com

^*****Саратовский государственный технический университет имени Гагарина Ю.А.,
Саратов, Россия, melnikovani @gmail.com

Аннотация. В работе описана процедура идентификации математической модели датчика давления, необходимой для минимизации затрат на его сертификацию. В основе модели используется метод интерполяции полиномами и бикубическими сплайнами. Приведены примеры реализации процедуры для реальных датчиков.

Ключевые слова: модель, датчик, двумерная интерполяция, сплайн, полином, метод наименьших квадратов.

IDENTIFICATION OF MATHEMATICAL MODEL FOR PRESSURE SENSOR USING CUBIC SPLINE INTERPOLATION

S.A. Kuzin^*, D.N. Sokolov^**, P.A. L’vov^***, D.A. Bulykin^****, N.I. Melnikova^*****

^*Yuri Gagarin State Technical University of Saratov,
Saratov , Russia, misha-q@mail.ru

^**Yuri Gagarin State Technical University of Saratov,
Saratov , Russia, yasyukn@ mail .ru

^*** OJSC «Signal» Engels Experimental Design Bureau named after A.I. Glukharev,
Engels, Saratov Region, Russia, peter.lvov@gmail.com:

^****Yuri Gagarin State Technical University of Saratov,
Saratov , Russia, d.bulykin@gmail.com

^****Yuri Gagarin State Technical University of Saratov,
Saratov , Russia, melnikovani@gmail.com

Abstract. Identification procedure of pressure sensor mathematical model, which is used in order to minimize a sensor certification cost, is described. This model is based on bicubic spline by the least square fitting of the signal samples taken from the sensor during its calibration. The examples of real data interpolation are presented.

Keywords: model, sensor, 2D interpolation, spline, polynomial, least square method.

Введение

Датчики давления (ДД) — перспективное направление развития первичных преобразователей. Они применяются во многих отраслях промышленности: энергетике, химической промышленности, машиностроении [1, 2]. Значительную часть предприятий, выпускающих ДД, составляют предприятия оборонно-промышленного комплекса [3–8]. Рост заказов на поставки измерительного оборудования требует увеличения объемов выпуска ДД. Поэтому на этих предприятиях выполняется переход к автоматизированному производству [9–13].

В рамках решения задачи автоматизации на производстве создаются системы контроля технологических процессов и испытания ДД. Эти системы предназначены для определения и контроля параметров ДД в нормальных и экстремальных климатических условиях [10, 13–18].

Основные функции системы:

· управление технологическим оборудованием;

· сбор/обработка данных;

· электрическое питание ДД;

· задание требуемого давления и обеспечение необходимой для испытаний температуры;

· ввод/отображение информации.

В состав аппаратной части системы входят:

· PXI 1042 — стойка (вмещает восемь слотов) с интегрированным контроллером на базе процессора Intel с предустановленной ОС Windows 7;

· модуль интерфейса Arinc 429 PXI 429-3U-16;

· вакуумный насос BECKER U-3.6;

· задатчик давления Mensor CPC8000 — осуществляет подачу испытательного давления на ДД;

· климатические камеры (камера тепла ESPEC PHH-101M, камера холода ESPEC MC-811) — обеспечивают требуемые значения испытательных температур;

· программируемый источник питания (АКИП 1118) — обеспечивает питание ДД, проходящих процесс стабилизации;

· коллектор — осуществляет распределение испытательного давления между определенным числом ДД.

Механические характеристики ДД существенно зависят от температуры, что приводит к возникновению значительной температурной составляющей погрешности измерений [19]. При этом требования к точности измерений информации постоянно повышаются. Для реализации в таких системах предлагается метод компенсации температурной составляющей погрешности измерений, производимых с помощью интеллектуальных ДД (ИДД) [12–14].

После производства ИДД необходимо сертифицировать на соответствие точности измерений. Эта процедура требует значительных затрат для предприятия. Как правило, сертификации ИДД предшествует его градуировка или калибровка, которая заключается в построении математической модели выходного сигнала датчика в зависимости от измеряемого давления и температуры окружающей среды. Однако используемые в настоящее время методики калибровки, заключающиеся в двумерной интерполяции выходного сигнала ДД с помощью полиномиальных зависимостей [12–14, 19], адекватно описывают рассматриваемое явление только с помощью полиномов достаточно высоких порядков (7–9). Поэтому находить коэффициенты этих зависимостей по методу наименьших квадратов (МНК) сложно из-за высокой размерности матриц и накапливающихся ошибок вычислений. В связи с этим предлагается метод построения математической модели ДД с помощью интерполяции его выходного сигнала бикубическими сплайнами для последующего тестирования датчика до сертификации и выявления погрешности (неопределенности) измерений.

Постановка задачи

Изначально предполагается, что датчик рассчитан для проведения измерений в известном диапазоне давлений [P_min, P_max] и известном диапазоне температур [T_min, T_max]. Также предполагается, что контроллер давления и климатические камеры, входящие в состав установки, позволяют устанавливать данные параметры внутри указанных диапазонов с заданной точностью.

Поскольку вид функциональной зависимости u = f(P,T), связывающей выходной сигнал датчика u с измеряемым давлением P и температурой окружающей среды T, не известен, то математическую модель f можно найти только приближенно в результате экспериментальных исследований с помощью методов аппроксимации характеристик датчика, полученных опытным путем. Для аппроксимации используются полиномиальные зависимости, в частности, кубические сплайны [20]. Также предполагается наличие ошибок измерения выходных сигналов u, т.е. реально измеряется следующая величина:

y = u + x,

где x — некоторая случайная погрешность измерения.

Для снижения влияния случайных ошибок измерения на точность искомой математической модели следует в каждой отдельной исследуемой экспериментально точке плоскости с координатами (P_j,T_i) проводить не одно измерение сигнала с выхода датчика, а серию из K измерений и вычислять осредненное значение сигнала в данной точке [12, 13].

На этапе получения экспериментальных данных диапазон давлений [P_min, P_max] равномерно разбивается на N_P поддиапазонов (интервалов), а диапазон температур [T_min, T_max] – на N_T поддиапазонов. Использовалась методика поиска математической модели выходного сигнала ДД, описанная в работах [12–14, 21–24], где предложено сначала найти зависимости 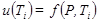, PÎ[P_min, P_max] для всех выбранных значений T_iÎ [T_min, T_max], (i = 0, 1,..., N_T; T₀ = T_min, 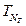= T_max), аппроксимировав их полиномом некоторой степени n, а далее искать зависимости коэффициентов полученного полинома от температуры.

На основании снятых экспериментальных данных можно аппроксимировать характеристику датчика 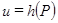интерполяционным полиномом, степень которого n подбирается с использованием известных методов математической статистики [25–28]:

u = h(P) = 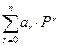. (1)

Далее зависимость каждого коэффициента a_r от температуры определяется в виде полинома вида:

a_r = a_r(T) = 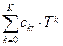, (r=0, 1,…, n), (2)

где K — порядок модели; c_kr — коэффициенты регрессии, оценки которых вычисляются и впоследствии заносятся в память микропроцессора ИДД.

Оказалось, что для исследуемых ДД зависимость выходного сигнала от входного измеряемого давления хорошо описывалась полиномом второй степени. Результаты, полученные при поиске зависимостей коэффициентов этого полинома от температуры по методике, описанной в [12–14], показали, что порядок моделей (2) получается достаточно высоким (K = 7¸9) и сильно разнится даже для однотипных датчиков из одной партии. Поэтому было решено искать зависимости коэффициентов полинома (1) от времени путем аппроксимации экспериментальных данных кубическими сплайнами, которая является частным случаем кусочно-полиномиальной интерполяции. Для этого весь рассматриваемый диапазон температур [T_min, T_max] разбивается на M поддиапазонов, на каждом из которых зависимость коэффициента полиномиальной регрессии a_r ищется в виде полинома степени не выше третьей.

a_r(T) = S_r(T) = 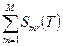, (r=0, 1,…, n), (3)

где функции S_mr(T) являются полиномами степени не выше третьей, описывающими зависимость коэффициента a_r в поддиапазоне с номером m. На остальных поддиапазонах эта функция равна нулю (рис. 1). То есть:

S_mr(T) = 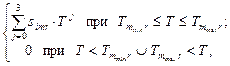, (r=0, 1,…, n), (4)

где 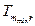и 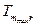— соответственно, наименьшая и наибольшая температуры для диапазона с номером m.

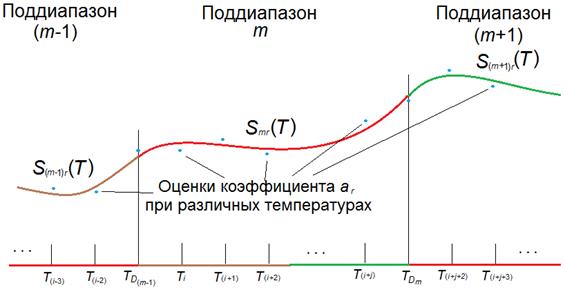
Рис. 1. Аппроксимация зависимости коэффициента a_r кубическими сплайнами S_mr(T)
в различных поддиапазонах. Вне «своего» диапазона функции S_mr(T) = 0; 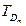— «граничные температуры» выбранных диапазонов

При этом функция S_r(T) должна быть непрерывной и иметь первую производную во всем диапазоне [T_min, T_max]. Если положить, что весь диапазон разбивается на поддиапазоны в температурных точках 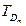так, что T_min = 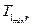, 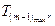= = 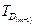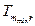, 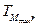= T_max,
m = 2,...,M, то должны выполняться следующие условия на границах поддиапазонов:

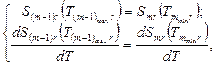(m=2, 3,…, M). (5)

Задача заключается в идентификации на основе полученных экспериментальных данных математической модели выходного сигнала ДД (1), когда математические модели коэффициентов регрессии задаются соотношениями (3), (4) и удовлетворяют граничным условиям (5).

Дата добавления: 2021-07-19; просмотров: 136; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!