Механизм процесса вытяжки. Схема НДС
Рассмотрим наиболее полную схему вытяжки с прижимом круглой плоской заготовки.

1 – пуансон
2 – прижим
3 – матрица
4 – заготовка

Сам процесс вытяжки условно можно разбить на 3 стадии:
Первая стадия характерна ростом усилия и тем, что пластическая деформация охватывает только часть заготовки, а именно свободную часть – участок ab. Центральная и периферийная часть деформируются упруго. Переход их в пластическое состояние сдерживает сила трения. По мере опускания пуансона происходит утонение и упрочнение свободной части. Она становится способной передавать усилие на соседние элементы и переводить их в пластическое состояние. Кроме того на этой стадии происходит рост усилия за счет изменения угла, обеспечивающего вертикальную проекцию усилия на свободном участке. Рост усилия происходит не только за счет упрочнения, но и за счет изменения угла.
Наконец наступает момент, когда вся заготовка охвачена зоной пластической деформации. На участке kb происходит рост усилия только за счет упрочнения фланца заготовки, не смотря на то, что размеры фланца уменьшаются. Однако наступает момент, когда фланец упрочняется, а его размеры малы и сопротивление его уменьшается. В этот момент наступает максимум усилия. Как правило для глубокой вытяжки происходит полностью обхват заготовкой пуансона в радиусной части и матрицы в радиусной части.
|
|
|
Последняя стадия характеризуется тем, что очаг пластической деформации имеет место не фланце и радиусе закругления. При этом сила падает, так как уменьшается сопротивление фланца. Сечение имеет меньше напряжение, и эта часть переходит в упругую область.
Для небольших коэффициентов вытяжки возможно наличие упругих зон пластических деформаций в зоне дна.
Рассмотрим случай глубокой вытяжки на второй стадии, именно на этой стадии наблюдаются большие усилия и деформации.
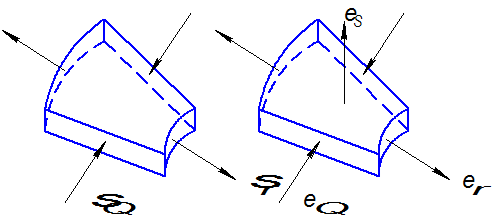
Участок ab – характерный участок, который присущ вытяжке.
Участок bc – участок радиусного закругления матрицы. На этом участке происходит утонение заготовки.

Участок cd – цилиндрический участок.
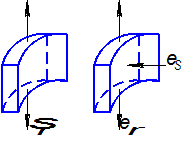
Участок de и ef – участки радиусных закруглений пуансона.

Определение напряжений и деформаций при вытяжке
Наиболее просто определяются деформации и напряжения на кромке фланца. На кромке фланца меридиональные напряжения приблизительно равны контактным  .
.
То есть имеем схему линейного напряженного состояния
 ,
,  ,
, 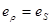 (изотропное тело).
(изотропное тело).
Геометрически это можно представить следующим образом:

Зная длины до и после длину окружности заготовки и фланца детали  можно найти тангенциальные деформации кромки.
можно найти тангенциальные деформации кромки.
|
|
|
 ,
,
при небольших деформациях данное равенство выполняется с погрешностью 2-3%.
Таким образом тангенциальная деформация кромки
 .
.
Для изотропного тела  , тогда
, тогда
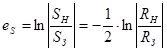 ,
,
 .
.
Толщина кромки
 .
.
Чем меньше наружный  , тем толще кромка.
, тем толще кромка.
Максимальная толщина кромки детали определяется как
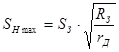 ,
,
где  – радиус детали.
– радиус детали.
Нас интересует в основном
- усилие процесса,
- геометрические размеры оснастки,
- величина утонения и утолщения заготовки.
Чтобы определить максимальную величину утонения следует предположить, что наибольшее напряжение и наибольшее утонение находятся в зоне границы радиусной и цилиндрической части. Это объясняется тем, что в этой зоне действуют наибольшие растягивающие напряжения от сопротивления участка фланца заготовки и радиусного участка.
На радиусной части заготовки напряжения уменьшаются за счет активных сил трения на пуансоне и напряжений от изгиба.

В случае, если поверхность радиусной части заготовки сильно отполирована, попала на нее смазка, максимальные напряжения переходят из цилиндрической части в радиусную.
|
|
|
По мере вытяжки это опасное сечение получает наибольшую величину утонения на стадиях, не достигших величины максимального усилия, и затем, переходит на цилиндрическую поверхность. В дальнейшем происходит обрыв дна при меньших значениях величин усилия в случае, если обработка поверхности радиусной части пуансона отлична от полировки. Надо стремится к тому, чтобы смазка в радиусной части не попадала на пуансон. Считают, что схема напряженного состояния – линейная.
Используем уравнение кривой упрочнения степенного вида:
 ,
,
где  ,
,  – интенсивности напряжений и деформаций
– интенсивности напряжений и деформаций
 ,
, 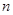 – константы механических свойств
– константы механических свойств
 ,
, 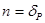 ,
,  .
.
Для линейной схемы напряженного состояния интенсивность напряжений равна 
 и
и 







Из условия постоянства объема  , не учитывая величину упругой деформации
, не учитывая величину упругой деформации  , где
, где  – толщина детали по средней поверхности (
– толщина детали по средней поверхности ( 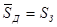 ), получаем условие равенства площадей при вытяжке:
), получаем условие равенства площадей при вытяжке:  .
.
Условие равенства площадей детали и заготовки положено в основу определения деформаций при вытяжке любого элемента.
Для осесимметричной вытяжки этот элемент является кольцевым.
Так как нас интересует усилие процесса вытяжки, предельный коэффициент, то следует определить величины деформаций для фланцевой части.
|
|
|
Схема к определению деформаций во фланце при осесимметричной вытяжке.
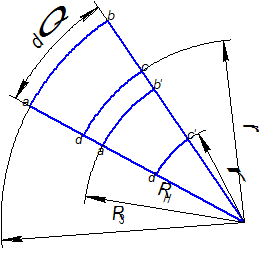
Выделим на фланце бесконечно малый элемент двумя плоскостями, проходящими через ось детали, перпендикулярно к площади фланца и образующие между собой  .
.
Если хотя бы один из размеров элемента имеет бесконечно малый размер, то элемент является бесконечно малым.
С другой стороны этот элемент образован двумя концентрическими окружностями, имеющими центр на оси симметрии и имеющие радиуса  и
и  . Получили элемент abcd. Рассмотрим стадию вытяжки, когда этот элемент находится в положении, ограниченном радиусами
. Получили элемент abcd. Рассмотрим стадию вытяжки, когда этот элемент находится в положении, ограниченном радиусами  и
и  .
.
Деформация любых тангенциальных точек определяется, если мы знаем длину до и после деформацию
 ,
,
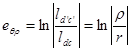 .
.
Длина 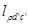 задается
задается  .
.
Длина исходного состояния этого элемента  .
.
Находим величину тангенциальной деформации любого элемента с координатой  , если известна длина этого элемента до деформации или известны его координаты.
, если известна длина этого элемента до деформации или известны его координаты.
Если известна зависимость  , то мы получаем величину деформации
, то мы получаем величину деформации  от независимой координаты
от независимой координаты  .
.
Связь между  и
и  находится из условия равенства площадей рассматриваемых элементов до и после деформации.
находится из условия равенства площадей рассматриваемых элементов до и после деформации.
 ,
,
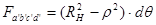 ,
,
 ,
,
 ,
,
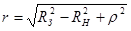 .
.
Теперь можем найти  .
.
Для того, чтобы определить две другие деформации 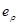 и
и  используют уравнение связи напряжений и деформаций.
используют уравнение связи напряжений и деформаций.
 ,
,
 (
(  плоская схема напряженного состояния),
плоская схема напряженного состояния),
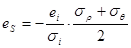 .
.
Используя методику, предложенную Поповым, Зубцовым, Маловым, будем считать, что соотношение напряжений в процессе формообразования величина постоянная:

и не зависит от упрочнения и изменения толщины.
Другими словами, рост напряжений за счет упрочнения в обоих случаях происходит пропорционально одному и тому же коэффициенту
 .
.
Если меняется толщина заготовки, то меняются и величины напряжений
 .
.
Это условие позволяет определить деформации по отношению  и используя уравнения связи (найденных без упрочнения и изменения толщины) по известной одной из деформаций, найти другую деформацию.
и используя уравнения связи (найденных без упрочнения и изменения толщины) по известной одной из деформаций, найти другую деформацию.
 .
.
Найдем напряжения, действующие на фланце без учета упрочнения и изменения толщины.

Составим уравнение равновесия на бесконечно малый элемент фланца заготовки.
Составим уравнение равновесия сил, действующих на координату  . На две другие координаты смысла составления уравнений нет, так как они обращаться в тождество.
. На две другие координаты смысла составления уравнений нет, так как они обращаться в тождество.
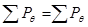
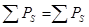
0=0 0=0
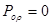
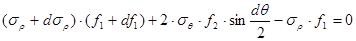
Раскрыв скобки уберем величины, которые на порядок меньше остальных, а также учтем, что  , тогда получим
, тогда получим
 ,
,
 (1)
(1)
Найдем значения площадей:
 , (2)
, (2)
 . (3)
. (3)
Подставив (2) и (3) в (1) получим:
 (4)
(4)
Уравнение (4) содержит 2 неизвестных  и
и 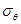 .
.
Условие пластичности по максимальным касательным напряжениям:
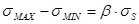 . (5)
. (5)
 определяет схему напряженного состояния, в нашем случае
определяет схему напряженного состояния, в нашем случае  .
.
 ,
,
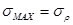 ,
,
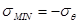 .
.
Условие пластичности (без учета упрочнения)(5) запишется следующим образом:
 (6)
(6)
Подставив в (4) уравнение (6), получим дифференциальное уравнение с разделяющимися переменными:
 . (7)
. (7)
Проинтегрировав уравнение (7) получим:
 .
.
Граничные условия:  , тогда постоянная интегрирования
, тогда постоянная интегрирования
 .
.
В результате получим:
 .
.
При 
 будет максимальным.
будет максимальным.
 ,
,  ,
,  .
.
Дата добавления: 2019-07-15; просмотров: 316; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
