Аналогичным образом представляем вектор градиента давления
grad P= 
(2.3)
Тогда выражение (2.2) можно представить
`V = 
. (б)
Сравнивая выражения (а) и (б), получаем 
. (2.4)
Уравнения (2.4), определяющие выражения для скоростей фильтрации флюида по закону Дарси в направлении координатных осей, называются уравнениями движения флюида.
Заметим,что в уравнениях (2.4) под давлением Р имеется в виду приведенное давление Р * =Р + g Z , где Р- давление пьезометрическое.
Для горизонтального пласта в уравнениях (2.4) давление Р есть давление пьезометрическое.
Перепишем уравнения (2.4) через пьзометрическое давление Р с учетом влияния силы тяжести, что имеет место при фильтрации в наклонных пластах.
; 
; 
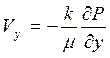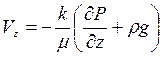, (2.5)
где ось Z - направлена вертикально вверх .
В теории фильтрации оказывается удобным ввести функцию Ф(x,y,z,), называемую потенциалом скорости фильтрации и определяемую выражением:
. (2.6)
Тогда уравнения движения (2.5) с учетом (2.6) запишутся в виде:
, 
, 
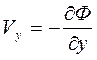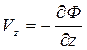. (2.7)
Таким образом, потенциалом скорости фильтрации называется функция Ф(x,y,z,), производная которой с обратным знаком вдоль линии тока равна скорости фильтрации V (x,y,z,).
С учетом (2.6) вектор скорости фильтрации (2.2) принимает вид:
`V = -grad Ф (2.8)
|
|
|
Выражения (2.7) и (2.8) представляют наиболее общую форму выражения линейного закона фильтрации и учитывают влияние силы тяжести на фильтрацию.
Уравнение неразрывности (сплошности)
Фильтрационного потока
Выведем уравнение неразрывности (сплошности) фильтрационного потока сжимаемого флюида в деформируемой пористой среде (самый общий случай). Для этого выделим в пористой среде элементарный объем в виде параллелепипеда с ребрами dx, dy, dz (рис. 5), причем длины ребер во много раз больше поперечных размеров поровых каналов.
Рис.5
В рассматриваемом общем случае неустановившегося движения сжимаемой жидкости (флюида) скорость фильтрации `V и плотность жидкости r являются функциями координат и времени, т.е.
`V = `V(x,y,z,t), r = r(x,y,z,t,).
Проекции на ось X массовых скоростей фильтрации в точках А и А1, расположенных в центрах боковых граней ab и a1b1, соответственно равны
rVx, и (rVx)1 = rVx +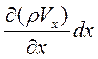 
.
Заметим, что в силу малости выделенного объема и его граней можно считать, что плотность r и скорость фильтрации `V распределены на гранях ab и a1b1 равномерно и равны значениям их в точках А и А1 соответственно.
|
|
|
Масса флюида, вытекающего в выделенный элемент через левую грань ab за малый промежуток времени dt, равна rVx*dydzdt.
Масса флюида, вытекающего из выделенного объема через правую грань a1b1 за этот же отрезок времени dt, равна
.
Тогда изменение массы флюида в объеме выделенного элемента aba1b1 за отрезок времени dt за счет потока вдоль оси Х будет равна:
dMx = [ (rVx)1 - (rVx) ] dydzdt = 
dxdydzdt.
Рассматривая фильтрацию флюида в направлении осей Y и Z, получим аналогичные выражения для изменения массы в элементарном объеме за счет потока вдоль этих осей в виде:
dMy = 
dxdydzdt, dMz = 
dxdydzdt .
Тогда общее изменение (накопление) массы флюида в объеме выделенного элемента aba1b1 за время dt будет равно:
dM = dMx + dMy + dMz ,
т.е. dM = - 
* dxdydzdt . (2.9)
С другой стороны, масса флюида, находящегося в рассматриваемом поровом объеме элемента aba1b1, равна
M = rmdxdydz ,
где m - коэф. пористости пласта.
Изменение массы флюида в этом же элементарном объеме aba1b1 за время dt можно записать так (объем элемента dxdydz фиксирован)
dM = 
. (2.10)
Приравнивая выражения (2.9) и (2.10) и сокращая их на dxdydzdt, получаем уравнение неразрывности фильтрационного потока.
. (2.11)
|
|
|
С физической точки зрения уравнение неразрывности (2.11) представляет собой уравнение материального баланса фильтрующейся жидкости (флюида) и выражает закон сохранения массы.
Заметим дополнительно, что уравнение неразрывности (2.11) справедливо только в том случае, когда внутри выделенного элемента пласта нет источников или стоков; это означает, что жидкость или газ движутся в продуктивном пласте без разрывов в сплошности потока и что в поле скоростей фильтрации нет особых точек (например, скважин), в которых жидкость (газ) может «исчезать» или «появляться». При движении жидкостей (газов) в пласте к скважинам это уравнение (2.11) справедливо всех точках пласта вне скважины.
Выражение в левой части уравнения (2.11) представляет собой дивергенцию вектора массовой скорости r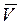 
и кратко записывается так:
.
Поэтому уравнение неразрывности (2.11) принимает краткую запись
. (2.12)
Дата добавления: 2019-07-15; просмотров: 139; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!