Движение вершины и центра треугольника Рело
Попробуем построить траектории движения двух характерных точек треугольника Рело при качении его по плоской горизонтальной поверхности. Такими точками будут одна из вершин треугольника и его геометрический центр. Моделирование одного полного оборота треугольника Рело показано на рисунке.

Рис.14
На фигурах 2, 6, 10 треугольник катится по поверхности окружности, на фигурах 4, 8, 12 треугольник переваливается через вершину, на остальных фигурах происходит смена характера движения треугольника с качения на переваливание и наоборот. Рассмотрим движение вершины треугольника. На фигурах 1, 2, 3 помеченная вершина движется линейно, по прямой (Рис. 10). Фактически помеченная вершина является центром вращения окружности, элементом которой является поверхность стороны треугольника Рело. На фигуре 3 помеченная вершина меняет траекторию движения с прямолинейной на траекторию движения по окружности с радиусом, равным длине стороны, по которой он движется на фигурах 3, 4, 5.
На фигуре 5 происходит смена траектории движения вершины. На фигурах 5, 6, 7 вершина движется по трохоиде точки, находящейся на поверхности окружности с радиусом, равным длине стороны треугольника.На фигурах 7, 8, 9 меченная вершина является точкой перевалатреугольника, она жестко лежит на поверхности. Фигуры 9, 10, 11 – опять трохоида и 11, 12, 1 – движение по окружности. По аналогии эти фигуры описаны выше. Меченая вершина возвращается в исходную точку. Треугольник Рело совершил полный оборот.
|
|
|

Рис.15 Движение вершины треугольника.

Рис.16 Движение центра треугольника.

Рис.17
Очень важной является траектория движения геометрического центра треугольника. Если обозначить длину стороны треугольника через R, то расстояние от вершины до геометрического центра будет равно R/  . На фигурах 3 – 4 – 5, 7 – 8 - 9, 11 – 12 – 1 (Рис.16) центр движется по дугам с радиусом именно R/
. На фигурах 3 – 4 – 5, 7 – 8 - 9, 11 – 12 – 1 (Рис.16) центр движется по дугам с радиусом именно R/  . На фигурах же 1 – 2 – 3, 5 – 6 – 7, 9 – 10 – 11 центр движется по трохоиде, причем расстояние от центра катящейся окружности (не путать с геометрическим центром треугольника, Рис. 15) до траектории искомой точки опять же равно R/
. На фигурах же 1 – 2 – 3, 5 – 6 – 7, 9 – 10 – 11 центр движется по трохоиде, причем расстояние от центра катящейся окружности (не путать с геометрическим центром треугольника, Рис. 15) до траектории искомой точки опять же равно R/  .
.
Площадь треугольника Рело
Одна из задач моей работы: доказать, что из всех фигур постоянной ширины d треугольник Рело имеет наименьшую площадь.

Для начала найдем площадь треугольника Рело:
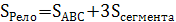
 ;
;
 ;
;

Следовательно, площадь треугольника Рело равна

Попробуем доказать, что треугольник Рело имеет наименьшую площадь. Обозначим через n количество сторон многоугольника.
Пусть дан какой-то правильный n–угольник (с нечетным числом сторон), следовательно, его шириной будет наибольшая из диагоналей (в данном случае их две).
|
|
|

(при n 
 ),
),  .
.
Оценим  и площадь треугольника Релло:
и площадь треугольника Релло:
 ,
,  >
> 
Следовательно,  больше площади треугольника Рело, а равносторонний, треугольник является многоугольником с наименьшим числом вершин (сторон). Значит, с увеличением числа вершин многоугольника площадь фигуры постоянной ширины, в которую вписан этот многоугольник, будет увеличиваться.
больше площади треугольника Рело, а равносторонний, треугольник является многоугольником с наименьшим числом вершин (сторон). Значит, с увеличением числа вершин многоугольника площадь фигуры постоянной ширины, в которую вписан этот многоугольник, будет увеличиваться.
Попробуем доказать, что треугольник Рело имеет наименьшую площадь через n— количество сторон многоугольника.
Доказательство.
Итак, площадь треугольника Рело равна  .
.
Пусть дан правильный многоугольник со стороной а. О — центр вписанной и описанной окружности. ОА=ОD; ОН  АD;
АD;  АОD=
АОD=  (n-число сторон), т.к. треугольник равнобедренный, ОН –биссектриса угла АОD.
(n-число сторон), т.к. треугольник равнобедренный, ОН –биссектриса угла АОD.

Следовательно,
 АОН=
АОН= 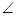 НОD;
НОD;  АОН:
АОН: 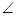 АОН=
АОН=  ; АН=
; АН=  , то
, то  .
.
 .
.
Диаметром многоугольника является его наибольшая диагональ (в данном случае их две). Рассмотрим центральный угол АОВ и вписанный в окружность угол АМВ (рис. 21), то 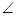 АОВ=2
АОВ=2 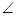 АМВ,
АМВ, 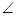 АМВ=
АМВ=  . AM=MB, то по теореме косинусов
. AM=MB, то по теореме косинусов
 , то
, то

Площадь фигуры, в которую вписан правильный многоугольник состоит из площади многоугольника и суммы площадей равных сегментов. Площадь сегмента равна
|
|
|

(Sсегмента=Sсектора  Sтреугольника АМВ).
Sтреугольника АМВ).


Остается доказать, что это выражение будет всегда больше площади треугольника Рело, т.е. больше чем  . Для этого вычтем из площади треугольника Рело площадь фигуры постоянного диаметра, в которую вписан правильный многоугольник и докажем, что эта разность при n>3 всегда будет отрицательной:
. Для этого вычтем из площади треугольника Рело площадь фигуры постоянного диаметра, в которую вписан правильный многоугольник и докажем, что эта разность при n>3 всегда будет отрицательной:

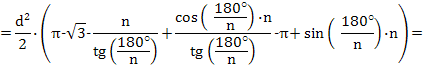

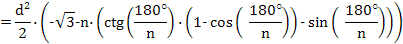
Итак, при любом n>3

Следовательно, разность площади треугольника Рело и площади фигуры постоянного диаметра, в которую вписан правильный многоугольник, отрицательна.Из всех фигур постоянной ширины треугольник Рело имеет наименьшую площадь.
Применение треугольника Рело
Дата добавления: 2019-07-15; просмотров: 175; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
