Закон Ома (в обобщённой форме )
Закон Ома применяется для расчёта токов и напряжений в отдельных ветвях цепи или для одноконтурной замкнутой цепи, не имеющей разветвлений.
При написании закона Ома следует прежде всего выбрать произвольно некоторое положительное направление тока.
Для ветви, состоящей только из сопротивлений и не содержащей ЭДС (см. рис.1 для ветви ba), при положительном направлении тока от (·) b к (·) a имеем:
 , где
, где
φ b , φa – потенциалы точек (узлов a,b);
Uba – разность потенциалов между точками b и a;
Rba - ??? сопротивление цепи, Rba= R1+ R2

Рис.1
Для ветви, состоящей из сопротивлений и ЭДС (ветвь acb), рис.1 ток:
 , где
, где
Uab – напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока;
ΣE – алгебраическая сумма ЭДС, находящаяся в этой ветви
Применение законов Кирхгофа
1. Устанавливается условно положительное направление тока.
2. Выбираются независимые контуры (контур, содержащий хотя бы один новый элемент).
3. Составляются уравнения по I закону Кирхгофа. Их число равно:
 (1)
(1)
где Ny – число узлов;
Nн – число источников напряжений, если они расположены между узлами, не имеющими сопротивлений.
4. Составляется уравнение по II закону Кирхгофа:
 (2)
(2)
где NB – число ветвей, Ny – число узлов;
NT – число источников тока, если они расположены между узлами, не имеющими проводимостей.
При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры, т.е. не содержащие источников тока.
|
|
|
Выбирается направление обхода контуров (произвольно).
При записи левой части равенства ЭДС, направления которых совпадают с выбранными направлениями обхода (независимо от направления тока, протекающего через них), принимаются положительными, а ЭДС, направленные против выбранного обхода, - отрицательными.
При записи правой части равенства со знаком «плюс» берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода (независимо от направления ЭДС в этих ветвях), и со знаком «минус», падения напряжения в тех ветвях, в которых положительное направление тока противоположно направлению обхода.
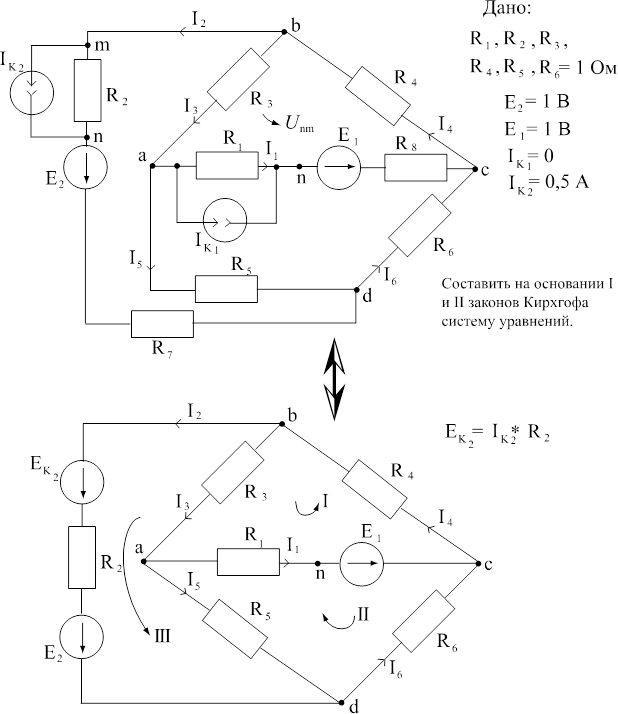
Решение:
К I = Ny – 1 – Nн = 4 – 1 – 0 = 3
Выбираем (·)a, (·)b, (·)c.
( ·) a: I3 – I1 = 0
( · )b: I4 – I2 – I3 = 0
( · )c: I6 + I1 – I4 = 0
KII = NB – (Ny – 1) – NT = 6 – (4 – 1) – 0 = 3
R3 I3 + R1 I1 + R4 I4 = E1 (I)
R1 I1 – R5 I5 – R6 I6 = E1 (II)
R2 I2 + R6 I6 + R4 I4 (III)
Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений исходное напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения Umn можно написать уравнение для контура mncb или nmbc:
|
|
|
Umn + I4 R4 + I3 R3 = E1 или - I3 R3 – Umn – I4 R4 = - E1
откуда легко можно найти искомое напряжение (необходимо при рассмотрении метода узловых потенциалов)
Дата добавления: 2019-07-15; просмотров: 171; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
