Нагрузки на подвеску автомобиля
Нагрузки на упругий элемент:
Зависимая подвеска (рис. 18, а). Нагрузка зависит от реакции Rzна колесо и веса неподрессоренных масс Gн.м:
PP = Rz — 0,5 G н.м
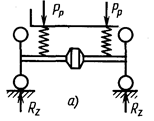

Рисунок 18. Расчетная схема для определения нагрузок на упругие элементы подвески
При этом прогиб упругого элемента равен перемещению колеса относительно кузова f р = f к .
Независимая подвеска.
Для двухрычажной подвески (рис. 19, а)нагрузка на упругий элемент
Pp = ( Rz — G 'к) l / a ,
где G 'к — вес колеса и направляющего устройства.
А прогиб fp = f к a / l .

Рисунок 19. Расчетная схема для определения нагрузок на упругие элементы подвески
Пружины в качестве основных упругих элементов широко применяются в подвесках легковых машин повышенной проходимости и в качестве вспомогательных элементов, например ограничителей или корректирующих устройств, на других машинах. В первом случае используются цилиндрические пружины, витые из прутка круглого или прямоугольного сечения; характеристика их линейна. Для ограничителей хода применяются конические пружины.
Усилие, сжимающее пружину, определяется кинематической схемой подвески.

Рисунок 20. Расчетная схема подвески с цилиндрической пружиной
Pn = (Pi ai,)/bi
Усилие Рn может быть выражено также следующим образом:
Pn = λּcn ,
Pnmax = λmaxּcn ,
где λ m ах — максимальная деформация пружины; сn — жесткость пружины.
|
|
|
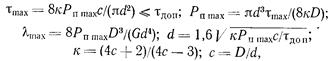
где τ m ах — максимальное напряжение в пружине; d — диаметр прутка; D — средний диаметр пружины; τдоп — допускаемое напряжение; τдоп = 600-700 МПа.
2.2 Колёса и шины автомобиля
Колесный движитель представляет собой устройство, преобразующее работу двигателя в поступательное движение машины. Он состоит из трех основных частей: шины, обода и ступицы.
Анализ и оценка конструкции автомобильных шин и колес

Рисунок 21 - Радиальный разрез покрышки
1— каркас; 2 — брекер; 3 — протектор; 4 — боковина; 5 — борт; 6 — носок борта; 7 — основание борта; 8 — пятка борта; 9 — бортовая лента; 10 — бортовая проволока; 11 — обертка; 12 — наполнительный шнур; H — высота профиля покрышки; H1 — расстояние от основания до горизонтальной осевой линии профиля; H2 — расстояние от горизонтальной оси до экватора; В — ширина профиля; B6— корона; R — радиус кривизны протектора; D — наружный диаметр шины; d — посадочный диаметр шины; h — стрела дуги протектора; С — ширина раствора бортов; а — ширина борта.
Полуоси, балка и поворотный кулак автомобиля
Т.к. автомобиль ВАЗ-2108 является переднеприводным значит у него не заднего моста.
При прямолинейном движении значения моментов M и сил P принимаются максимальными. Рассмотрим изгиб балки вертикальной плоскости (рис. 22).
|
|
|
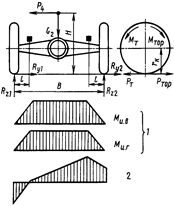
Рисунок 22. Расчетная схема балки ведущего моста и эпюры моментов
Изгибающий момент
Ми.в = R '' z 1 l = R '' z 2 l ,
где R''z1и R''z2 — нормальные реакции опорной поверхности за вычетом веса Колеса GK.
Нормальные реакции опорной поверхности от нагрузки на мост G2
Rz 1 = Rz 2 = m 2 G 2 /2,
где m2 = 1,1...1,2— коэффициент перераспределения нагрузки по мостам.
Изгиб картера в горизонтальной плоскости под нагрузкой от силы тяги Рт
Ми.г = P т1 l = P т2 l ,
где Рт1=Рт2 = Rz 1 φ = Rz 2 φ, (φ = 0,8...0,9 — коэффициент сцепления шин с опорной поверхностью).
Момент, скручивающий балку, Мкр = P т1 r к = R т2 r к (rк—радиус качения колеса).
Результирующее напряжение от изгиба и кручения для круглого трубчатого сечения
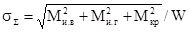 ,
,
где W = 0,2( D 4 — d 4 )/ D — момент сопротивления трубчатого сечения.
Для прямоугольного и коробчатого сечения напряжения в вертикальной и горизонтальной плоскостях определяют раздельно и суммируют арифметически: σи = Mи.в / Wв + Mи.г /Wг. Напряжения кручения при этом не суммируют:
τ = M кр / W кр = Рт1 r к / W кр = Рт2 r к / W кр ,
Максимальные напряжения изгиба относятся к крайним волокнам сечения, а напряжения кручения к средним волокнам сечения.
|
|
|
При заносе балку моста рассчитывают на изгиб в вертикальной плоскости, считая при этом Рт1=Рт2 = 0.
Изгибающие моменты в вертикальной плоскости
M и1 = R " z 1 l — Py 1 rK ; M и2 = R " z 2 l + Py 1 rK .
Ry1 и Ry2 — боковые реакции при заносе:
Ry 1 = R ' z 1 φ; R ' z 1 = 0,5 G 2 (1 + 2 φ H / В);
Ry 2 = R ' z 2 φ; R ' z 2 = 0,5 G 2 (1 — 2 φ H / В);
где R'z1 и R'z2 — нормальные реакции опорной поверхности при заносе.
Условно принимается φ = 1.
Эпюры моментов от R'z и Py1 строятся раздельно, а затем складывают. Опасное сечение картера находится в месте крепления рессоры: здесь напряжение изгиба σи = Ми / W .
При динамическом нагружении изгибающий момент в вертикальной плоскости:
Ми = Rz 1 K д l ,
где Кд=1,5...3 — коэффициент динамичности.
Напряжение изгиба σи = Ми / W.
Для балок мостов, литых из стали и чугуна, [τи] = 300 МПа, для штампованных из стального листа [τи] = 500 МПа.
Определение нагрузок и расчет переднего моста производят так же, как и заднего моста. При торможении коэффициент перераспределения нагрузки на передний мост m1 = 1,1.„1,2. Необходимо учитывать переменное сечение балки: двутавровое в средней части и после рессорной площадки постепенно переходящее в круглое. Вертикальные реакции Rzl = Rz2 = m1G1/2,где G1 — нагрузка на передние колеса.
|
|
|
Для балки управляемого моста жесткость важна для сохранения углов установки колес. Жесткость ведущего моста влияет на условия зацепления зубчатых передач, на нагрузку подшипников и на нагруженность полуосей.
Прогиб балки равен силе в заданном сечении, отнесенной к жесткости сечения f = Pи / (EJx).Балка нагружена в местах крепления рессор. Переменное сечение балки затрудняет расчет. В таких случаях или упрощают схему и ведут расчет по наиболее опасному сечению, или усложняют расчет, применяя метод конечных элементов.
Прогиб балки грузовых автомобилей достигает 2...3 мм.

Рисунок 23. Расчетная схема поворотной цапфы
Поворотный кулак(рис. 23). Расчет ведется для тех же трех случаев нагружения: торможения при прямолинейном движении, заноса и динамического нагружения.
При торможении суммарный момент изгиба в вертикальной плоскости
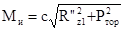 ,
,
где R '' z 1 = Rzl — G к ; Ртор = Rz φ — тормозная сила на колесе, нагружающая цапфу.
Напряжение изгиба:
σи = Ми / W .
При заносе напряжение изгиба на цапфе при Ртор = 0
σи1=( R '' z 1 — Ry 1 r к )/ W ; σи2=( R '' z 2 с — Ry 2 r к )/ W .
При динамическом нагружении напряжение изгиба
σи = Rz 1 с Кд / W ,
где коэффициент динамичности Кд = 1,5...3.
Для стали 30Х и 40Х допускаемое напряжение [σи] = 500 МПа.

Рисунок 24. Расчетная схема шкворня
Шкворень. Расчетные режимы, применяемые при расчете шкворня, те же, что и при расчете цапф. Наклоном шкворня пренебрегаем.
При торможении реакции, нагружающие верхний R'шк и нижний R''шк концы шкворня, обусловленные действием:
реакции Rz :
R 'шк1 = R ''шк1 = Rzl / ( a + b );
силы Ртор :
R' шк 2 = Ртор b / (a + b); R'' шк 2 = Ртор a / (a + b);
реактивной силы:
R' шк 3 = Р 1 b / (a + b); R'' шк 3 = Р 1 a / (a + b),
где P 1 = Ртор l / l 1 ;
тормозного момента Мтор = Ртор r к
R 'шк4 = Ртор r к / ( a + b ).
Суммарная сила, действующая на нижний конец шкворня,
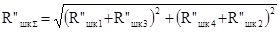 .
.
Суммарная сила, действующая на верхний конец шкворня:
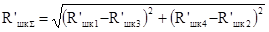 .
.
На шкворень действуют напряжения:
изгиба σи = R ''шкΣ d / W и ;
среза τcp = 4 P ''шкΣ / ( πd 2 шк );
смятия σсм = R ''шкΣ /( d шк l шк ).
Для расчета принимают наибольшее из значений Р'шкΣ, Р''шкΣ.
При заносе действуют только поперечные силы.
От вертикальной реакции:
R' шк 1 = R''z1 l / (a + b); R'' шк 1 = R''z1 l / (a + b),
где R '' z 1(2) = = R '' z 1(2) — G к .
От боковой силы Ry и от момента, создаваемого этой силой:
левый шкворень R 'шк1 = R ''шк1 = Ry 1 l / ( a + b )
правый шкворень R 'шк1 = R ''шк1= Ry 2 l / (а+ b ).
Суммарная нагрузка на левом шкворне:
R' шкΣ = [Ry1(r к —b) — R''z1 l] / (a + b);
R'' шкΣ = [Ry1(r к + a) — R''z1 l] / (a + b).
Суммарная нагрузка на правом шкворне:
R 'шкΣ = [ Ry 2 ( r к — b ) — R '' z 2 l ];
R'' шкΣ = [Ry2(r к + a) — R''z2 l] / (a + b).
Напряжения определяются так же, как и при торможении.
При динамическом нагружении напряжение изгиба в вертикальной плоскости
σи = Rz 1 с Кд / W .
Расчетные режимы полуосей. Полуразгруженную полуось рассчитывают на изгиб и кручение так же как балку моста для трех случаев нагружения: прямолинейного движения, заноса и динамического нагружения.
При прямолинейном движении — результирующий изгибающий момент полуоси в вертикальной и горизонтальной плоскостях
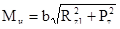
момент кручения полуоси:
Мкр = Рт r к ;
сложное напряжение:
 .
.
При заносе изгибающие моменты на правом и левом колесах
M и l = Ry 2 r к — Rz 2 b ; M и2 = Ry 2 r к + R " z 2 b .
При динамическом нагружении
вертикальная нагрузка:
Rz 1 K д = Rz 2 K д ;
горизонтальная нагрузка:
Rz 1 K д φ = Rz 2 K д φ;
скручивающая нагрузка:
Рт r к = Мкр = Rz 1 K д φ r к = Rz 2 K д φ r к .
При расчете полуразгруженной полуоси плечо изгиба b определяется как расстояние между плоскостями, проходящими через центр опорной площадки колеса и через центр опорного подшипника.
Полностью разгруженные и разгруженные на три четверти полуоси рассчитывают только на кручение и определяют их жесткость.
Касательное напряжение кручения:
τ = Рт r к / 0,2 d 3 ; Мкр = Рт r к .
Угол закручивания полуоси:
θ = (180 / π )( M кр l / GJ кр );
здесь момент инерции Jкр = πd4/32, модуль сдвига G = 85 ГПа. Угол закручивания обычно ограничивается θ = 9...15° на 1 м длины полуоси. Меньшее значение угла закручивания характеризует повышенную жесткость, большее значение — склонность к колебаниям и резонансным явлениям.
Полуразгруженная полуось разрушается в опасном сечении под подшипником. Здесь полуось должна быть утолщена. Разгруженная полуось разрушается в месте начала шлицев. Рекомендуется осадка конца полуоси под шлицевой конец для увеличения диаметра опасного сечения.
Несущая система автомобиля
Дата добавления: 2019-07-15; просмотров: 1351; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
