Друге правило дослідження функції на екстремум.

Щоб дослідити функцію 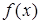на екстремум, треба:

1) знайти стаціонарні точки заданої функції;

2) знайти похідну другого порядку в стаціонарній точці. Якщо в стаціонарній точці , то є екстремальною точкою для функції , а саме, точкою мінімуму, якщо , і точкою максимуму, якщо .

Приклад 6. Дослідити функцію на екстремум:

Розв’язання. Знаходимо похідну: . Прирівнюємо похідну до нуля і розв’язуємо рівняння:

Дістаємо стаціонарні точки:

Знаходимо похідну другого порядку:

Підставляємо у вираз для 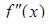значення і :

Отже, є точкою максимуму, — точкою мінімуму функції , причому максимум і мінімум відповідно дорівнюють .

Приклад 7. Дослідити функцію на екстремум:

Розв’язання. Знаходимо похідну першого порядку:

Прирівнюємо похідну до нуля і розв’язуємо утворене рівняння:

Звідси знаходимо стаціонарні точки:

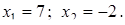
Знайдемо похідну другого порядку:

Тоді

Отже, в точці функція має мінімум , а в точці — максимум .

Знаходження найбільшого і найменшого значень функції

Нехай на відрізку задано неперервну функцію , тоді за теоремою Вейєрштрасса функція на даному відрізку досягає свого найбільшого і свого найменшого значень. Це може статися як всередині відрізка, так і на його кінцях.

Якщо функція набуває найбільшого значення всередині відрізка, то це найбільше значення є одночасно і один з максимумів (локальний максимум) заданої функції.

Теж саме можна сказати про найменше значення функції. Але може бути й так, що одне із значень функція набуває всередині відрізка, а друге на одному з кінців.

Звідси випливає спосіб знаходження точок, в яких функція набуває найбільшого та найменшого значення на відрізку :

1) знайти критичні точки функції;

2) обчислити значення функції в критичних точках, які належать відрізку, і на кінцях відрізка;

3) найбільше (найменше) значення серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку .

Приклад 1. Знайти найбільше і найменше значення функції на відрізку .

Розв’язання. Знаходимо стаціонарні точки. Для цього знайдемо похідну:

Прирівнюючи цю похідну до нуля і розв’язуючи рівняння

дістаємо стаціонарні точки: . Точок, в яких функція не існує, немає.

Обчислюємо значення функції в точках , а також на кінцях відрізка, тобто в точках :

Отже, найбільше значення , найменше є .

Приклад 2. Знайти найбільше та найменше значення функції на відрізку .

Розв’язання. Функція є неперервною на відрізку . Знаходимо екстремуми функції. Обчислюємо першу похідну:

Функція має дві критичні точки: . Але не належить відрізку . В точці функція має максимум, причому . Обчислюємо значення функції на кінцях відрізка: .