Дослідження функції за допомогою похідних
Монотонність функції. Екстремум функції
Припустимо, щофункція 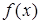 визначена на деякому проміжку (а; b), а
визначена на деякому проміжку (а; b), а 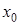 є внутрішньою точкою цього проміжку.
є внутрішньою точкою цього проміжку.
Функція 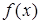 називається зростаючою в точці
називається зростаючою в точці  , якщо існує окіл
, якщо існує окіл  точки
точки 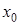 , який міститься в проміжку (а; b) і такий, що
, який міститься в проміжку (а; b) і такий, що  , для всіх
, для всіх  і
і  для всіх
для всіх  .
.
Якщо функція  диференційовна на інтервалі (а; b) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі (а; b) невід’ємна, тобто
диференційовна на інтервалі (а; b) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі (а; b) невід’ємна, тобто  .
.
Якщо функція 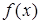 диференційована на інтервалі (а; b) і ії похідна
диференційована на інтервалі (а; b) і ії похідна  для
для 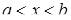 , то ця функція зростає (спадає) на інтервалі (а; b).
, то ця функція зростає (спадає) на інтервалі (а; b).
Функція 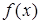 називається спадною в точці
називається спадною в точці  , якщо існує окіл
, якщо існує окіл  точки
точки  , який міститься в проміжку (а; b) і такий, що
, який міститься в проміжку (а; b) і такий, що  , для будь якого
, для будь якого 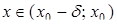 і
і  для будь якого
для будь якого  .
.
Якщо існує окіл 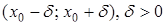 точки
точки  , який міститься в проміжку (а; b) і такий, що
, який міститься в проміжку (а; b) і такий, що  для всіх
для всіх  , то точка
, то точка  називається точкою максимуму функції
називається точкою максимуму функції 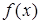 , а саме число
, а саме число 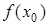 називається максимумом функції
називається максимумом функції 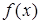 в точці
в точці  .
.
Якщо існує окіл 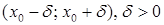 точки
точки  , який міститься в проміжку (а; b) і такий, що
, який міститься в проміжку (а; b) і такий, що  для всіх
для всіх  , то точка
, то точка  називається точкою мінімуму функції
називається точкою мінімуму функції 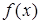 , а саме число
, а саме число 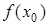 називається мінімумом функції
називається мінімумом функції 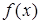 в точці
в точці  .
.
Точки максимуму й мінімуму функції називають ще екстремальними точками, а максимум і мінімум називають екстремумом функції.

Приклад 1. Довести, що функція 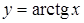 є зростаючою в інтервалі
є зростаючою в інтервалі 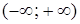 .
.
Розв’язання. Знаходимо похідну функції  :
:

У кожній точці  маємо
маємо 
Отже, за попередньою теоремою робимо висновок, що функція  є зростаючою в кожній точці даного інтервалу.
є зростаючою в кожній точці даного інтервалу.
|
|
|
Приклад 2. Довести, що показникова функція  ,
,  ,
, 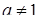 , в інтервалі
, в інтервалі 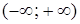 при
при  є спадною, а при
є спадною, а при  — зростаючою.
— зростаючою.
Розв’язання. Знаходимо похідну функції 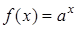 :
:

Внаслідок того, що  при
при  , то
, то

Отже, при  функція
функція  є спадною.
є спадною.
Якщо  , то
, то 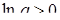 і тому
і тому  . Таким чином,
. Таким чином, 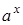 у цьому випадку є зростаючою.
у цьому випадку є зростаючою.
Приклад 3. Знайти інтервали зростання і спадання функції:
 .
.
Розв’язання. Знаходимо похідну:

При будь якому  маємо
маємо  .
.
Отже, функція  на всій числовій осі
на всій числовій осі  є зростаючою.
є зростаючою.
Приклад 4. Знайти інтервали зростання і спадання функції:
 .
.
Розв’язання. Знаходимо похідну:
 .
.
При  маємо
маємо  , при
, при  маємо
маємо  .
.
Отже, в інтервалі  функція
функція  спадає, а в інтервалі
спадає, а в інтервалі  зростає.
зростає.
При цьому точка 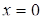 є точкою мінімуму заданої функції.
є точкою мінімуму заданої функції.
Приклад 5. Знайти інтервали зростання і спадання функції:
 .
.
Розв’язання. Знайдемо похідну:

Знайдемо точки, в яких  . Це є всі точки, де
. Це є всі точки, де  . Розв’яжемо цю нерівність:
. Розв’яжемо цю нерівність:
 або
або  .
.
Отже, в інтервалі 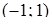 функція зростає. Тоді в інтервалах
функція зростає. Тоді в інтервалах  ,
,  функція спадає.
функція спадає.
Робимо висновок, що точка  є точкою є точкою мінімуму, а точка
є точкою є точкою мінімуму, а точка  — точкою максимуму заданої функції, при цьому мінімум функції дорівнює
— точкою максимуму заданої функції, при цьому мінімум функції дорівнює  , максимум
, максимум  .
.
Необхідна ознака існування екстремуму
|
|
|
Якщо функція 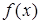 у внутрішній точці
у внутрішній точці  проміжку
проміжку  має екстремум, то в цій точці похідна
має екстремум, то в цій точці похідна  , якщо вона існує, дорівнює нулю.
, якщо вона існує, дорівнює нулю.
Внутрішня точка  проміжку
проміжку  називається стаціонарною точкою функції
називається стаціонарною точкою функції  , якщо в цій точці
, якщо в цій точці  . Стаціонарні точки і точки, в яких похідна не існує, називаються критичними точками функції.
. Стаціонарні точки і точки, в яких похідна не існує, називаються критичними точками функції.
Перше правило дослідження функції на екстремум
Щоб дослідити функцію 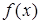 на екстремум, треба:
на екстремум, треба:
1) знайти стаціонарні точки заданої функції, для цього слід розв’язати рівняння  , з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;
, з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;
2) знайти точки, в яких похідна  не існує (функція
не існує (функція 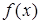 в ціх точках існує). Якщо критичних точок функція
в ціх точках існує). Якщо критичних точок функція 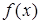 не має, то вона не має й екстремальних точок. Така функція не має екстремуму. Якщо критичні точки є, то їх треба досліджувати далі, для чого:
не має, то вона не має й екстремальних точок. Така функція не має екстремуму. Якщо критичні точки є, то їх треба досліджувати далі, для чого:
3) у кожній критичній точці перевірити зміну знака похідної першого порядку.
Якщо  при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо
при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо  змінює знак з – на +, то ця критична точка є точкою мінімуму.
змінює знак з – на +, то ця критична точка є точкою мінімуму.
Якщо при переході через критичну точку знак похідної не змінюється, то розглядувана критична точка не є екстремальною точкою заданою функції.
|
|
|
Теорема. Нехай точка  є стаціонарною для функції
є стаціонарною для функції 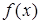 і нехай в цій точці існує похідна другого порядку
і нехай в цій точці існує похідна другого порядку  , яка не дорівнює нулю
, яка не дорівнює нулю  . Тоді, якщо
. Тоді, якщо  , то
, то  є точкою мінімуму, якщо
є точкою мінімуму, якщо  , то
, то  є точкою максимуму функції
є точкою максимуму функції 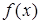 .
.
Дата добавления: 2019-07-15; просмотров: 181; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
