Парність, непарність функцій. Періодичність функцій
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДОНБАСЬКИЙ ГІРНІЧО-МЕТАЛУРГІЙНИЙ ІНСТИТУТ
Т.М. Сукач
Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової системи
Навчальний посібник
Алчевськ, 2004
Передмова
Вища математика, як навчальна дисципліна, є однією з осноних при підготовці висококваліфікованих кадрів у вищих технічних та інших навчальних закладах. Диференціальне числення є основним розділом курсу вищої математики в цілому.
Без засвоєння основних положень, на яких базується диференціальне числення, не можна на належному якісному рівні застосовувати теорію та методи вищої математики при розв’язанні ряду задач з різних галузей знань (при вивченні фізики, електротехніки, інших інженерних та економічних спеціальностей).
Матеріал посібника поділено на 4 глави:
1) Функція, границя, неперервність; 2) Диференціальне чис-лення функції однієї змінної; 3) Дослідження функції за допомогою похідних; 4) Диференціальне числення функцій багатьох змінних.
Кожна глава складається з параграфів, яки містять короткі теоретичні відомості та приклади розв’язання типових вправ. Для самостійної роботи студентів наводиться комплекс типових вправ з відповідями. Наприкінці кожної глави запропоновано зразки контрольних робот з теми, питання до колоквіуму, завдання семестрової роботи студентів. Наведена інструкція що до модульно-рейтингового контролю знань студентів при вивченні даного розділу вищої математики.
|
|
|
Зміст посібника, а також рівень навчальних вимог до знань студентів відповідає програмі курсу “Вища математика для інженерно-технічних, економічних спеціальностей вищих навчальних закладів, студентів технічних коледжів”.
Функція, границя, неперервність
Функція. Область визначення функції
Нехай маємо множину Х дійсних чисел. Якщо кожному числу 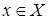 за певним правилом або законом поставлено у відповідність одне дійсне число у, з множини
за певним правилом або законом поставлено у відповідність одне дійсне число у, з множини  , то говорять, що на множені Х визначено функцію і записують
, то говорять, що на множені Х визначено функцію і записують  .
.
При цьому множина Х називається областю визначення або областю існування функції; х називають аргументом або незалежною змінною; у називають залежною змінною або функцією; 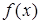 називають значенням функції в точці х;
називають значенням функції в точці х;  — множина, до якої належить значення функції.
— множина, до якої належить значення функції.
Множину всіх значень функції, яких вона набуває при 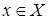 , називають областю значень функції.
, називають областю значень функції.
Приклад 1. Знайти область визначення функції
 .
.
Розв’язання. Функція у існує, якщо підкореневий вираз невід’ємний. Тому область визначення знаходиться з нерівності:
|
|
|

 |
Таким чином, областю визначення даної функції є відрізок  .
.
Приклад 2. Знайти область визначення функції
 .
.
Розв’язання. Функція визначена, якщо  .
.
Таким чином, область визначення даної функції є сукупність інтервалів:
 та
та  .
.
Приклад 3. Знайти область визначення функції
 .
.
Розв’язання. Функція визначена, якщо

Тобто
 |
 .
.
Парність, непарність функцій. Періодичність функцій
Нехай функцію  задано на проміжку
задано на проміжку  , який є симетричним відносно початку координат. Це може бути або нескінченний інтервал
, який є симетричним відносно початку координат. Це може бути або нескінченний інтервал  , або скінчений інтервал
, або скінчений інтервал 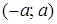 , або відрізок
, або відрізок  , де а — будь-яке дійсне число.
, де а — будь-яке дійсне число.
Функція  , визначена на проміжку
, визначена на проміжку  , називається парною, якщо для будь-якого
, називається парною, якщо для будь-якого  виконується рівність
виконується рівність

Графік парної функції симетричний відносно осі ординат.
Функція  , визначена на проміжку
, визначена на проміжку  , називається непарною, якщо для будь-якого
, називається непарною, якщо для будь-якого  виконується рівність
виконується рівність

Графік непарної функції симетричний відносно початку координат.
Приклад 1. Нехай  , де
, де  . Згідно з відомою властивістю даної функції,
. Згідно з відомою властивістю даної функції,
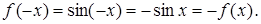
Отже, 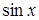 є непарною функцією.
є непарною функцією.
Приклад 2. Нехай  , де
, де 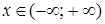 . Відомо, що
. Відомо, що

Отже,  є парною функцією.
є парною функцією.
Приклад 3. Дослідити на парність чи непарність функцію
|
|
|

Знайдемо область визначення функції:

Знайдемо  :
:
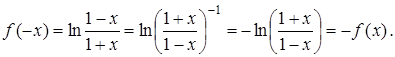
Одержали, що 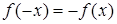 , тобто
, тобто  — непарна.
— непарна.
Функція  , визначена на всій числовій осі, називається періодичною, якщо існує число
, визначена на всій числовій осі, називається періодичною, якщо існує число  таке, що для всіх
таке, що для всіх  виконується тотожність
виконується тотожність

Число Т при цьому називається періодом функції  , а саму функцію називають Т-переодічною.
, а саму функцію називають Т-переодічною.
Якщо число Т є періодом функції  , то й число –Т є також періодом
, то й число –Т є також періодом  :
:

Якщо  — періодична функція з періодом Т, то функція
— періодична функція з періодом Т, то функція  , де
, де 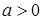 , є періодичною з періодом
, є періодичною з періодом  .
.
Зокрема, якщо розглянути функцію  , де
, де  — сталі, то періодом цієї функції є число
— сталі, то періодом цієї функції є число 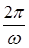 .
.
Зауважимо, що функцію  у фізиці називають гармонікою, число
у фізиці називають гармонікою, число  називають амплітудою,
називають амплітудою,  — циклічною частотою, а
— циклічною частотою, а  — початковою фазою гармоніки.
— початковою фазою гармоніки.
Приклад 4. Знайти період функції  .
.
Розв’язання. Функція  має період
має період  , тому функція
, тому функція  має період
має період  .
.
Приклад 5. Знайти період функції  .
.
Розв’язання. Функція 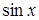 має період
має період  , тому
, тому  має період
має період  .
.
Приклад 6. Знайти період функції  .
.
Розв’язання. Функція  має період
має період  .
.
Тренувальні вправи
Дослідити на парність чи непарність функції:
1. 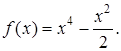 [Парна]
[Парна]
2.  [Непарна]
[Непарна]
3.  [Парна] 4.
[Парна] 4.  [Парна]
[Парна]
5.  [Ні парна, ні непарна]
[Ні парна, ні непарна]
Дата добавления: 2019-07-15; просмотров: 219; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
