Классы смежности и классы сопряженных элементов

Пусть G – группа, H – ее подгруппа.

Определение 1. Всякое множество Hg (т. е. совокупность всех элементов hg, где h пробегает H, g – фиксированный элемент группы G) называется правым смежным классом группы G по подгруппе H. Аналогично определение левого смежного класса gH.

Каждый элемент смежного класса называется его представлением. Так, элемент g – представитель класса Hg, поскольку из-за наличия в группе Н единицы е группы G элемент g=egÎHg.

Будем считать подгруппу H первым правым смежным классом. В результате группу G можно представить в виде объединения правых смежных классов:

Hg₁+Hg₂+…+Hg_m=G (3)

Выражение (3) называется правосторонним разложением группы G по подгруппе H.

Рассмотрим пример. В группе C₃_V выберем подгруппу { , }={ }₂, считая ее первым правым смежным классом. Возьмем элемент и по таблице Кэли группы C₃_V найдем второй правый смежный класс { , } ={ , }. Элемент не входит в оба класса, и с помощью его получаем третий правый смежный класс { , } ={ , }. Таким образом, правостороннее разложение группы C₃_V по подгруппе { }₂ имеет вид

C₃_V={ , }+{ , }+{ , }. (4)

Аналогично левостороннее разложение группы C₃_V по подгруппе { }₂ имеет вид

C₃_V={ , }+{ , }+{ , }. (5)

Существенно, что левостороннее разложение (5) не совпадает с правосторонним разложением (4).

Теорема Лагранжа. Порядок подгруппы H конечной группы G является делителем порядка группы G.

Теорема Лагранжа облегчает нахождение подгруппы группы G. Надо искать подгруппы группы G не любых порядков, а порядков, равных делителям порядка группы G. Например, группа C₃_V имеет порядок 6, а у числа 6 делителями являются числа 1, 2, 3, 6. Мы уже нашли подгруппы группы C₃_V, имеющие приведенные порядки – это подгруппы { }, { }, { }₃={ , , } и сама C₃_V. Подчеркнем, что если число m является делителем порядка группы G, то отсюда не следует, что в группе G есть подгруппа порядка m, т. е. теорема, обратная теореме Лагранжа, не имеет места.

Определение 2. Элементы а и b группы G называются сопряженными, если существует элемент х из группы G такой, что выполняется равенство

a=x^-1bx (6)

Например, в группе C₃_V согласно таблице Кэли этой группы, имеем = ^-1 = 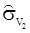, поэтом элементы и сопряжены с помощью элемента .

С помощью понятия сопряженности можно дать классификацию элементов группы G. Обозначим через Kg₁, Kg₂, …, Kg_t все классы сопряженных элементов. Всю группу G можно представить в виде

Kg₁+ Kg₂+ …+ Kg_t=K₁+K₂+…+K_t=G, (7)

где Kg_i=K_i; i=1, 2, …, t – непересекающиеся классы сопряженных элементов.

Найдем эти классы для группы C₃_V. Очевидно, что единица сама является классом сопряженных элементов, ибо всегда = . Обозначим этот класс R₁. Второй класс сопряженных элементов – это { , }, поскольку не сопряжено с и , а других возможностей нет. С помощью таблицы Кэли проверяется, что третий класс сопряженных элементов есть { , , }, в итоге

C₃_V= K₁+K₂+K₃={ }+{ , }+{ 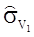, , } (8)

Факторизация групп

Пусть дана группа G и два подмножества M и N множества G.

Определение 1. Произведением подмножеств М и N группы G называется множество MN, состоящее из всевозможных произведений mn, где m пробегает множество M, а n – множество N.

Теорема 1. Произведение АВ двух подгрупп А и В группы G будет подгруппой группы G, если А и В перестановочны, т. е. если АВ=ВА.

Рассмотрим примеры. В группе C₃_V перемножим подгруппы { }₃ и { }₂. Используя таблицу Кэли для C₃_V, получаем, что C₃_V факторизуема: C₃_V={ }₃ { }₂. По таблице Кэли группы C₃_V находим { }₂{ }₂={ , , , }. Но это не подгруппа группы C₃_V. Следовательно, согласно теореме должно выполняться неравенство { }₂{ }₂¹{ }₂{ }₂. Действительно, перемножая, получим

{ }₂{ }₂={ , , , }.

Определение 2. Группа G называется прямым произведением подгруппы А и В, если элементы подгрупп А и В перестановочны: ab=ba, "aÎA, "bÎB и каждый элемент gÎАВ однозначно представляется в виде произведения g=ab. Обозначается прямое произведение подгруппы как G=A´B.

Определение 3. Подгруппа Н группы G называется циклической, порожденной элементом h, если все ее элементы являются степенями элемента h. Если же сама группа G совпадает со своей циклической подгруппой, то она называется циклической группой.

Элементом симметрии называется вспомогательный геометрический образ, характеризующий циклическую группу преобразования симметрии.

Теорема 2. Каждая конечная абелева группа G является прямым произведением конечных циклических групп, порядки которых являются степенями простых чисел.

Определение 4. Множество элементов a, b, c… группы G называется системой образующих групп G, если каждый элемент группы может быть представлен в виде произведения степеней элементов указанного множества

a^kb^lc^m…=g.

Например, для циклической группы { }₃ образующим элементом или генератором группы является элемент . У группы C₃_V два образующих элемента: и , в чем можно убедиться, рассматривая факторизацию C₃_V={ }₃´{ }₂.

Определение 5. Соотношения вида

a^pb^qc^r…=e,

связывающие образующие элементы группы G, называются ее определяющими соотношениями.

Совокупность всех образующих элементов и определяющих соотношений, полностью описывающих группу, называется генетическим кодом группы.

Например, группа { }₃ задается одним образующим элементом и одним определяющим соотношением = . Группа C₃_V задается двумя образующими и и определяющими соотношениями между ними вида

= , = , = (9)

Последнее соотношение после умножения его на можно записать в стандартном виде = . Именно способом задания группы объясняется обозначение группы C₃_V, так как операции симметрии и при определенных соотношениях между ними определяют группу C₃_V. Чтобы получить таблицу Кэли группы C₃_V, надо было пользоваться геометрической моделью молекулы NH₃. Зная же систему (9) определяющих соотношений, можно, например, найти, чему равно , если известно произведение . В самом деле, так как = , то умножая справа на , имеем = . Факторизация группы также значительно облегчается при задании группы с помощью генетического кода. Например, в полупрямом произведении C₃_V={ }₃´{ }₂ соотношение = задает автоморфизм группы { }₃, так как является ее образующим элементом. Поэтому, пользуясь тем, что автоморфизм переводит произведение элементов в произведение их образов, получаем уже автоматически