Формулы Коши (геометрические уравнения)

Стр 1 из 3Следующая ⇒

УПРУГОПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ ТРУБЫ ПОД ДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ

Чебоксары – 2006

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

ГЛАВА I. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ПЛАСТИЧНОСТИ

1.1 Основные понятия теории упругости

1.2 Уравнения равновесия

1.3 Формулы Коши

1.4 Линейный закон Гука

1.5 Условия пластичности

ГЛАВА II. ЗАДАЧА УПРУГОПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ТРУБЫ

2.1 Механическая постановка задачи

2.2 Математическая постановка задачи

2.3 Решение задачи

ВЫВОДЫ

ЛИТЕРАТУРА

ВВЕДЕНИЕ

Детали машин в процессе работы подвергаются внешним воздействиям.

В результате элементы этой детали изменяют форму и размеры, т.е. деформируются. Деформации после снятия нагрузки могут исчезать, а могут оставаться. Исчезающие деформации называются упругими, а остающиеся – остаточными (пластическими).

В данной работе рассматривается упругопластическая деформация трубы под действием равномерного внутреннего давления.

В первой главе приведены основные уравнения, используемые при решении поставленной задачи: основные понятия теории упругости, уравнения равновесия, формулы Коши, линейный закон Гука и условия пластичности.

Вторая глава посвящена решению поставленной задачи. Приводятся формулы для компонент напряжений и деформации в упругой и пластической зонах, также приводится трансцендентное уравнение для нахождения радиуса границы пластической и упругой областей. Задача решается в линеаризованном виде методом малого параметра.

ГЛАВА I . ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ И ПЛАСТИЧНОСТИ

Основные понятия теории упругости

В данном пункте получим классические уравнения деформирования в предположении, что среда эта – сплошная, однородная и изотропная, т.е. упругие свойства среды во всех направлениях одинаковы. Будем считать, что она линейно деформируема (для материала среды справедлив закон Гука), а перемещения и деформации тела достаточно малы.

При составлении уравнений механики деформируемого твёрдого тела выбирается соответствующая система координат. В зависимости от формы тела используются декартовые, полярные, цилиндрические координаты и другие.

При решении полной задачи удобно использовать полярную систему координат, в которой положение каждой точки определяется координатами r и (рис. 1.1).

Линейная дуговая координата s и угол связаны зависимостью 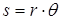, откуда следует соотношение между их дифференциалами .

Рассматриваемое тело находится под действием поверхностных нагрузок. В результате чего в теле появляются напряжения, которые, также как и поверхностные нагрузки, характеризуются интенсивностями. Под действием внешних нагрузок точки тела перемещаются в пространстве. Например, точка после деформации заняла положение . Полное перемещение зададим двумя компонентами: - в радиальном направлении, - в тангенциальном.

Для получения уравнений в полярной системе ординат мысленно выделим в окрестности некоторой точки тела элемент , , 1 (рис. 1.2).

На гранях этого элемента действуют напряжения, которые можно разложить на нормальную составляющую к грани (нормальное напряжение - , ) и касательную (касательное напряжение - , ).

Уравнения равновесия

Первая группа уравнений выражает условия равновесия элемента среды во взаимодействии с соседними элементами, их называют статическими уравнениями.

Вторая группа уравнений связывает деформации элемента тела с функциями, выражающими перемещение его точек. Они называются геометрическими уравнениями.

Последняя группа уравнений – это уравнения, которые выражают зависимость между напряжениями и деформациями элемента. Именно в этих уравнениях учитываются механические свойства материала, их называют физическими.

Рассмотрим указанные уравнения подробно.

Уравнения равновесия (статические уравнения)

Эти уравнения выражают равенство нулю сумм проекций всех элементарных сил, действующих на элемент , , 1 (рис. 1.2). Приняв напряжения, указанные на этом рисунке, за положительные, получим уравнения равновесия в виде

В этих равенствах учтены проекции сил, действующих на гранях , которые они дают вследствие наклона на малые углы . Косинусы этих малых углов приняты равными единице. Заменив в приведенных равенствах

, , , ,

учтя выражение для частных дифференциалов напряжений (нижние индексы у обозначения частных дифференциалов здесь опущены в целях упрощения записи)

, , , ,

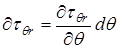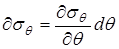а также сохранив и отбросив слагаемые высшего порядка малости, получим уравнение равновесия в полярных координатах:

Приравняв нулю сумму моментов сил, действующих на момент , , 1, относительно оси,проходящей через его центр перпендикулярно плоскости площадки , , и, отбросив слагаемые высшего порядка малости, получим закон парности касательных напряжений .

Формулы Коши (геометрические уравнения)

Эти уравнения устанавливают зависимость между перемещениями и деформациями. Для их вывода будем считать функции , заданными, а через них выразим деформации.

Геометрически деформация тела может быть представлена двумя группами простейших деформаций: деформацией растяжения - , и деформацией сдвига 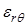, которые соответственно выражают относительные удлинения отрезков и :

, (рис. 1.3)

и изменение прямого угла между ними на угол сдвига :

(рис. 1.4)

Будем считать, что элемент тела сначала получил перемещение из точки в точку , как жесткое целое, а затем произошел сдвиг за счет поворота его граней на малые углы , , т.е. угол сдвига равен .

Для определения деформации рассмотрим отрезок длиной . Для малых перемещений и деформаций примем, что на изменение длины отрезка влияет лишь перемещение , а его малый наклон, в общем случае вызываемый перемещением , не изменяет его длины.

Обозначим: - частный дифференциал (линейная часть приращения) функции и при изменении координаты на .

, т.е.

Тогда

Аналогично

где производная по s заменена на производную по по соотношению , так как .

Для определения деформации рассмотрим рис. 1.4. Так как частные дифференциалы и , то

, .

Имеем угол сдвига

, где .

Деформации , составляют только часть полных деформаций и поэтому отмечены звездочкой. Другую часть этих деформаций получим, давая точкам элемента перемещения (рис. 1.5) и (рис. 1.6).