III.Отношения и функции

Стр 1 из 4Следующая ⇒

Федеральное агентство по образованию Тверской государственный технический университет Т.В. Асеева Дискретная математика Задания на контрольную работу Учебное пособие (для студентов первого курса специальности 22.01) вычислительные машины, системы, сети и комплексы) Тверь 20 15 УДК 510(075.8) ББК22.12я7 Асеева Т.В. Дискретная математика. Задания на контрольную работу:. Тверь: ТвГТУ, 2017, 19 с. Методические указания содержат перечень заданий для контрольной работы по курсу "Дискретная математика", читаемому студентам 1-го курса специальности ЭВМ во втором семестре. Контрольная работа выполняется студентами во втором семестре. Автор АСЕЕВА Т.В ã Тверской государственный технический университет, 2015 Требования к оформлению и срокам сдачи контрольной работы Задание на контрольную работу по Дискретной математике выдается студентам первого курса специальности ИВТ в первой неделе второго семестра. Контрольная работа выполняется в два этапа. В конце каждого этапа работа сдается на проверку преподавателю. Контрольная работа может быть оформлена либо в 12-листовой тетради, или распечатана на листах формата А4 по желанию студента. В тексте контрольной работы должны содержаться: · Номер раздела и задачи. · Текст условия задачи. · Решение с объяснением, таблицами, графическими иллюстрациями. Сроки сдачи этапов контрольной работы: · 8-я неделя второго семестра; · 17-я неделя второго семестра. Оценка выполненной работы учитывается при промежуточной аттестации студента, которая проводится в середине 2-го семестра. Полностью выполненная работа сдается на проверку преподавателю не позже 17-й недели 2-го семестра. Качество выполнения всей работы учитывается при сдаче экзамена. Оглавление I. Задание множеств. 4 II. Операции над множествами. 6 III. Отношения и функции. 8 IV. Специальные бинарные отношения. 10 V. Функции алгебры логики. 11 VI. Минимизация булевых функций. 13 VII. Элементы комбинаторики. 15 Варианты заданий на контрольную работу по дискретной математике. 18

I. Задание множеств

1.Задать перечислением элементов множество :

1.1.{x | x=y+z, y,z Î X, X={1,2}};

1.2. {y | y=x+z, x,z Î X, X={1,3}};

1.3. {y | x=y+z, x,z ÎX, X= {1,2}};

1.4. {x | x=1 ИЛИ x-2 Î X, X={1,2}};

1.5. {x |x=3 ИЛИ x-3 Î Y, Y={1,2}};

1. 6.{x |x=2 ИЛИ x-2 Î Z, Z={1,2}}.

2.Найти булеан множества и записать все его компоненты с помощью характеристической функции:

2.1. X = {1,2,3};

2.2. X = {a, b, {a,b}};

2.3. X=Æ;

2.4.X = { Æ,a,b}.

3. Задать перечислением элементов следующее множество:

3.1. X = { x | x=p´q, p,q-простые числа, p<5, q<7};

3.2. X = { x | x²(x²+2x-8)=0};

3.3. X = { x | x²-2x-3=0}.

4. Определить мощность множества:

4.1. Æ, {Æ}, X={x | x>5, xÎN};

4.2.{1,2,3}, {1,{2,3}}, {1,(2,3)}.

5. Обследование 100 студентов дало следующие результаты о количестве студентов, изучающих различные иностранные языки: испанский - 28, немецкий - 30, французский - 42, испанский и немецкий - 8, испанский и французский - 10, немецкий и французский - 5, все три языка - 3. Используя формулу включений/исключений, определите

· сколько студентов не изучает ни одного языка?

· сколько студентов изучает один французский язык?

6. При обследовании 100 студентов, были получены следующие данные о числе студентов, изучающих различные иностранные языки: только немецкий 18, немецкий, но не испанский 23, немецкий и французский 8, немецкий 26, французский 48, французский и испанский 8, никакого языка 24. Используя формулу включений/исключений, определите

· сколько студентов не изучает ни одного языка?

· сколько студентов изучают испанский язык?

· сколько студентов изучают немецкий и испанский языки, но не французский?

7. В отчете об обследовании 100 студентов, изучающих иностранные языки (См. задание 5), указывалось, что количество студентов, изучающих различные языки таково: все три языка 5, немецкий и испанский 10, французский и испанский 8, немецкий и французский 20, испанский 30, немецкий 23, французский 50. Инспектор, представивший этот отчет, был уволен. Почему? При обосновании ответа используйте формулу включений/исключений.

8. Известно, что из 100 студентов живописью увлекается 28, спортом - 42, музыкой - 30, живописью и спортом - 10, живописью и музыкой - 8, спортом и музыкой - 5, живописью, спортом и музыкой - 3. Используя формулу включений/исключений, определите

1. сколько студентов увлекается только спортом;

2. сколько студентов увлекается только живописью;

3. сколько студентов увлекается только музыкой;

4. определить число студентов, не увлекающихся ничем.

9. Пусть I = { a,b,c,d,e,f }, X = { a,b,c }, Y = {a,c,e,f }, Z = { d,e }. Определить множество, заданное формулой, перечислением элементов и с помощью характеристической функции:

9.1. X\(YÇZ).

9.2. (Х ÇZ)\`Y;

9.3. ( X È(Y ÇZ));

9.4. (X ÈY) Ç(X ÈZ));

9.5. ;

9.6.

9.7.

9.8. (X ÈY) ÇZ;

9.9. X È(Y ÇZ);

9.10. X\Z;

9.11. X\Z È Y\Z.

10. Справедливо ли утверждение : Æ = {Æ }?

11. Справедливо ли высказывание: если А Î В и В Î С, то А Î С? Привести примеры.

12. Пусть А, В,С - множества и С Í В. Доказать, что А È С Í А È В.

13. Пусть С и D не пустые произвольные множества. Определить C ÇD и C ÈD.

14. Какие из следующих утверждений справедливы:

14.1. 0 Î Æ;

14.2. Æ= {0};

14.3. |{ Æ}|=1;

14.4. {{ Æ}}={{{Æ}}};

14.5. |{{Æ}}|=2;

14.6. {Æ}ÍÆ;

14.7. ÆÍ{Æ};

14.8. ÆÍ I;

14.9. {Æ}Í{{Æ}}.

II. Операции над множествами

1.Для произвольных множеств X и Y доказать справедливость соотношений:

1.1.

1.2.

2.Даны множества А, В, С и СÍВ. Доказать, что

2.1. А Ç С Í А Ç В;

2.2. A È C Í A È B;

2.3. A\B Í A\C;

2.4. C\A Í B\A;

2.5. `B\AÍ`C\A.

3. Доказать, что если АÍВ, то Р(А)ÍР(В).

4. Доказать справедливость тождеств:

4.1. AÈB=AÈ(B\A);

4.2. (AÈB)\C=(A\C)È(B\C);

4.3. A\(B\C)=(A\B)È(AÇC);

4.5. A\(BÈC)=(A\B)\C;

4.6. AÈBÍCÛAÍC и BÍC;

4.7. AÍBÇCÛAÍB и AÍC;

4.8. AÇBÍCÛAÍ`BÈC;

4.9. (A\B)ÈB=AÛBÍA;

4.10. (AÇB)ÈC=AÇ(BÈC)ÛCÍA;

4.11. AÍBÞAÈCÍBÈC;

4.12. AÍBÞAÇCÍBÇC;

4.13. AÍBÞA\CÍB\C;

4.14. AÍBÞC\BÍC\A;

4.15. AÍB Þ `B Í`A ;

4.16. A È B = A Ç B Û A = B;

4.17. A =`B Û A Ç B = Æ и A È B = I;

4.18. A = B Û (A\B) È (B\A) = Æ.

5. Доказать, справедливость тождеств:

5.1. Р(А Ç В ) = Р(А) Ç Р(В);

5.1.

5.3. P(AÈB)={(A_i ÈB_i) | A_i ÎP(A), B_i ÎP(B)};

5.4. .

6. Какие утверждения верны для всех множеств А, В, С:

6.1. AÎ B и BÎ C Þ A Î C;

6.2. AÍ B и ВÎ С Þ АÎ С;

6.3. A Ç B Í`C и A È C Í B Þ A Ç C = Æ;

6.4. A¹B и B¹C Þ A¹C;

6.5. AÍ и BÍ Þ B=Æ.

7. Решить систему уравнений

где А, В, С - данные множества.

8. Решить систему уравнений

где А, В, С - данные множества.

9. Решить систему уравнений

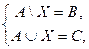
где А, В, С - данные множества, В Í А Í С.

10.Решить следующие системы уравнений:

10.1.

10.2.

10.3.

При каких А, В, С эти системы имеют решения?

11.Доказать, что :

11.1. (А ´ В) È (C ´ D) Í (AÈC) ´ (BÈD). При каких А,В,С получается равенство ?

11.2. (А È B) ´ C = (A ´С ) È (B´C);

11.3. А´ (BÈC) = (A´B) È (A´C);

11.4. (AÈB) ´ (CÈD) = (A´C) È (B´C) È (A´D) È (B´D);

11.5. А ´ (B\C) = (A ´ B)\ (A ´ C);

11.6. А ´ B = (A ´ D) Ç(C ´ B) Û A Í C и B Í D;

11.7. I² \ (A ´ B) = [(I\A) ´ I] È [I ´ (I\B)];

11.8. ( ;

11.9. ;

III.Отношения и функции

1. Пусть [a,b],[c,d] Í R. Найти геометрическую интерпретацию множеств:

1.1. [a ,b] x [c,d];

1.2. [a,b] x {c,d};

1.3. {a,b} x [c,d];

1.4. {a,b} x {c,d};

1.5. {0,1}³;

1.6. {-1,0,1}²;

1.7. {1,2,3} x [a,b];

1.8. [1,2] x {a,b,c};

1.9. {a,b,c} x {1,2};

1.10. {a,b,c} x [0,1];

1.11. {a} x {1};

1.12. {1,2} x {a};

1.13. {a,b} x {-1,0,1};

1.14. {-1,0,1} x {a,b,c};

1.15. {-1,0,1} x [a,b];

1.16. {-1,1,3} x {2,4};

1.17. {-1,1,3} x [2,4].

2. Определить всеми возможными способами бинарное отношение на множестве А ={1,2,3,4,5} и указать его свойства, если

2.1. xry Û (x-y) - четно;

2.2. xry Û x=y ;

2.3. xry Û х делит у;

2.4. xry Û x>y;

2.5. xry Û x<y;

2.6. xry Û x=y;

2.7. xry Û x³y;

2.8. xry Û x£y;

2.9. xry Û остаток от деления х на у равен 1.

3. Задать всеми возможными способами бинарное отношение r на множестве {-4,-3,-2,-1,0,1,2,3,4},определенное следующим образом:

3.1. аrb Û a<b;

3.2. аrb Û a делитель b;

3.3. аrb Û a>b;

3.4. аrb Û a³b;

3.5. аrb Û a=b;

3.6. аrb Û b-1 < a < b+2.

4. Пусть X={2,4,6,8}, xry Û x<y, x,yÎX. Определить отношения r и r^-1 перечислением элементов.

5. Определить перечислением элементов отношения Ì и Í, заданные на булеане множества {a,b,c}.Изобразить диаграмму Хассе для отношения Í.

6.Сколько бинарных отношений можно задать на множестве {0,1}? Выписать все эти отношения, построить их графы. Выделить среди них все отношения эквивалентности, все отношения частичного порядка, а также все отношения являющиеся одновременно симметричными и транзитивными, но не рефлексивными.

7. Доказать, что операция композиции бинарных отношений ассоциативна.

8. Определить все возможные бинарные отношения на множестве {a,b} и найти среди них все отношения эквивалентности, а также все отношения являющиеся одновременно симметричными и транзитивными, но не рефлексивными.

9. Пусть А и В - конечные множества с мощностью m и n соответственно.

9.1. Сколько существует бинарных отношений между элементами этих множеств?

9.2. Сколько имеется 1-1 - функций из А в В ?

9.3. Сколько существует взаимно однозначных соответствий между А и В ?

10. Доказать, что если f есть функция из А в В и g есть функция из В в С , то f · g есть функция из А в С.

11. Пусть f и g - функции. При каких условиях

11.1. f ^-1 является функцией ;

11.2. f · g является взаимно однозначной функцией ?

12. Доказать, что для того, чтобы отношение rÍ А´В было взаимно однозначным соответствием между А и В, необходимо и достаточно, чтобы r·r^-1 = I_A и r^-1·r=I_B, где I_A и I_B - диагональ соответствующих множеств.

13. Сколько существует бинарных отношений, для которых r^-1=`r?

14. Пусть r - бинарное отношение на множестве А. Доказать, что r=I_A тогда и только тогда: когда r·r₁=r₁·r=r₁ для любого отношения r₁ на множестве А.

15. Доказать, что для любых бинарных отношений справедливы тождества:

15.1. r È r = r Ç r = r;

15.2. (r^-¹)^-¹= r;

15.3. (r₁È r₂)^-¹= r₁^-¹È r₂^-¹,

15.4. (r₁Ç r₂)^-1= r₁^-¹Ç r₂^-¹,

15.5.

16.Найти область определения, область значений, график отношения r, обратное отношение r^-¹, дополнение отношения`r, композиции r·r, r·r^-¹, r^-¹·r для отношения:

16.1. хrу Û х,у Î R и х £ 2у-4;

16.2. хrу Û х,у Î R и х +y<0;

16.3. хrу Û х,у Î R и 2х < 3y-1;

16.4. хrу Û х,у Î R и х £4y+5;

16.5. хrу Û х,у Î R и х /2 < (y+2)/4;

16.6. хrу Û х,у Î [-p/2, p/2], x ³ Sin y;

16.7. хrу Û х,у Î (0,1], y ³ ln x;

16.8. хrу Û х,у Î (0,10], y ³lg x;

16.9. хrу Û х,у Î R и х > 2y+1;

16.10 хrу Û x Î[-p/2,p/2], y Î R и y ³ tg x.

17. Доказать, что для любых отношений r₁ и r₂ справедливы соотношения:

17.1.