Вопросы и задачи для самоконтроля
1. Почему движение тела с одной неподвижной точкой иногда называют сферическим движением?
2. Сколько степеней свободы имеет тело с одной неподвижной точкой? Расскажите об углах Эйлера и корабельных углах.
3. Что понимается под мгновенной осью вращения тела при его сферическом движении? Какие кинематические характеристики при этом называются глобальными?
4. Как связаны локальные и глобальные кинематические характеристики при сферическом движении?
5. Как найти угловое ускорение в случае, если известен годограф вектора угловой скорости?
6. Подвижный конус 1 катится без проскальзывания по неподвижному конусу 2 так, что угловая скорость 
вращения вокруг вертикальной оси постоянна. Ось подвижного конуса в процессе движения остается горизонтальной. Угол при вершине неподвижного конуса 
; оси конусов составляют прямой угол. Получите формулы для угловой скорости 
и углового ускорения 
подвижного конуса.
7. Решите следующие задачи из [2]: 19.1, 19.14, 19.15, 24.26
Плоскопараллельное движение тела
Описание (задание) движения
В ряде случаев движение твердого тела происходит таким образом, что траектории всех его точек являются плоскими кривыми; плоскости их расположения параллельны либо совпадают. Например: маневрирование надводного судна без изменения посадки, качение цилиндра по плоскости, движение шатуна ОА кривошипно-шатунного механизма и т.п. (рис.5.1).
|
|
|
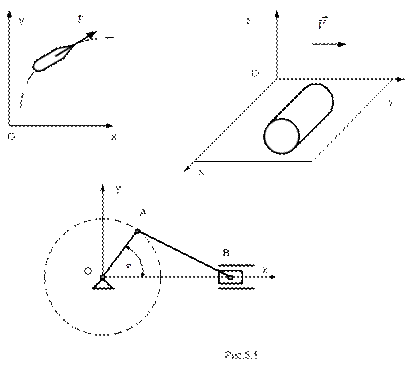
Движение твердого тела называется плоскопараллельным (плоским), если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Частными случаями плоского движения являются поступательное плоское движение и вращение вокруг неподвижной оси. Рассмотрим плоскопараллельное движение твердого тела, точки которого перемещаются в плоскостях, параллельных плоскости 
(рис.5.2). Проведем прямую 
, жестко связанную с телом и перпендикулярную указанной плоскости; все кинематические характеристики точек, принадлежащих прямой , одинаковы.
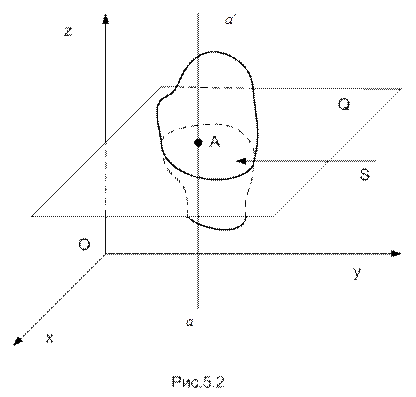
Отметим на прямой какую-либо точку А и проведем через нее плоскость 
, параллельную плоскости 
. Движение плоской фигуры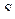 
, являющейся сечением тела плоскостью 
, полностью отражает движение рассматриваемого тела.
Известно (см. введение), что положение плоской фигуры на плоскости определяется тремя независимыми обобщенными координатами, так что число степеней свободы тела, совершающего плоскопараллельное движение (плоской фигуры, совершающей плоское движение), равно трем. Для описания (задания) движения плоской фигуры в неподвижной системе отсчета введем жестко связанную с фигурой координатную систему 
, а так же полусвязанную поступательно движущуюся координатную систему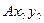 
, оси которой параллельны соответствующим осям неподвижной системы отсчета (рис.5.3).
|
|
|
Тогда положение фигуры 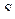на неподвижной плоскости определяется функциями
(5.1)
которые называются уравнениями движения плоской фигуры или уравнениями плоскопараллельного движения твердого тела.
Плоское движение рассматривают как результат сложения двух более простых движений. Первое из них происходит вместе с полусвязанной системой 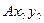(поступательное движение с кинематическими характеристиками точки 
, называемой в этом случае полюсом), а второе представляет собой вращение вместе с осями связанной системы относительно полусвязанной (вращение вокруг полюса). В такой трактовке, называемой методом полюса, первое уравнение в (5.1) определяет движение полюса, а второе описывает вращение плоской фигуры вокруг полюса (точнее, вокруг оси 
). Выбор в качестве полюса другой точки изменяет поступательное движение полусвязанной координатной системы; при этом глобальные кинематические характеристики вращательного движения остаются прежними (инвариантными относительно выбора полюса). В качестве иллюстрации, на рис.5.4 плоская фигура 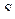и жестко связанный с нею отрезок 
переводится из одного положения в другое, в котором отрезок занимает положение 
.
|
|
|
Если за полюс выбирается точка , то отрезок сначала поступательно перемещается в положение 
, а затем поворачивается на угол 
вокруг полюса до положения . Если за полюс выбирается точка 
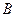, то отрезок сначала поступательно перемещается в положение 
, а затем поворачивается на угол 
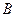вокруг полюса до положения 
. Из рисунка видно, что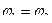 
.
Дата добавления: 2019-03-09; просмотров: 227; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!