ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
СТАТИКА
Задача C1
Жесткая рама (рис. C1.0 – C1.9, табл. C1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действуют пара сил с моментом М = 60 кНм и две силы, величины которых, направления и точки приложения указаны в таблице (например, в условиях № 1 на раму, действуют сила  под углом15° к горизонтальной оси, приложенная в точке D,и сила
под углом15° к горизонтальной оси, приложенная в точке D,и сила  под углом 60° к горизонтальной оси, приложенная в точке Е и т.д.).
под углом 60° к горизонтальной оси, приложенная в точке Е и т.д.).
Определить реакции связен в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять a = 0,5 м.
Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой, через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы  часто удобно разложить ее на составляющие
часто удобно разложить ее на составляющие  и
и  для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда
для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда  .
.




Пример С1. Жесткая пластина ABCD (рис. С1) имеет в точке А неподвижную шарнирную опору, a в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
|
|
|
 Дано: F = 25 кН, α = 60°, Р = 18 кН, γ = 75°, М = 50 кНм, β = 30°, а = =0,5 м.
Дано: F = 25 кН, α = 60°, Р = 18 кН, γ = 75°, М = 50 кНм, β = 30°, а = =0,5 м.
Определить: реакции в точках А и В, вызываемые действующими нагрузками.
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы: силу  пару сил с моментом М, натяжение троса
пару сил с моментом М, натяжение троса  (по модулю Т=Р) и реакции связей ,
(по модулю Т=Р) и реакции связей ,  ,
,  ,
, 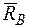 (реакцию неподвижной шарyирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
(реакцию неподвижной шарyирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
Таблица С1
| Силы |
|
|
|
| ||||||
|
|
|
|
| |||||||
| Номер условия | Точка приложения |

| Точка приложения |

| Точка приложения |
| Точка приложения |
| ||
| 0 1 2 3 4 5 6 7 8 9 | H - K - D - E - H - | 30 - 75 - 30 - 60 - 60 - | - D - K - H - D - E | - 15 - 60 - 30 - 60 - 75 | - E - H - - K - D K | - 60 - 30 - - 15 - 30 30 | K - E - E D - H - - | 60 - 30 - 60 75 - 15 - - | ||
|
|
|
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы  относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу
относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу  на составляющие
на составляющие  ,
,  (
(  ,
,  )и учтем, что
)и учтем, что  . Получим:
. Получим:
 ; (1)
; (1)
 . (2)
. (2)
 . (3)
. (3)
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ:  = – 8,5 кН,
= – 8,5 кН,  = – 23,3 кН,
= – 23,3 кН,  = 7,3 кН. Знаки указывают, что силы
= 7,3 кН. Знаки указывают, что силы  и
и  имеют направления, противоположные показанным на рис. С1.
имеют направления, противоположные показанным на рис. С1.
Задача С2
Конструкция состоит из жесткого угольника и стержня, которые в точке C или соединены друг с другом шарнирно (рис. С2.0 – С2.5) или свободно опираются друг о друга (рис. С2.6 – С2.9). Внешними связями, наложенными на конструкцию, являются: в точке А или шарнир или жесткая заделка; в точке В или невесомый стержень ВВ' (рис. 0 и 1) или гладкая плоскость (рис. 2 и 3) или шарнир (рис. 4 – 9); в точке D или невесомый стержень DD ' (рис. 1, 2, 7) или шарнирная опора на катках (рис. 9).


На каждую конструкцию действуют: пара сил с моментом М = =60 кНм, равномерно распределенная нагрузка интенсивности q =
=20 кН/м и еще две силы. Величины этих сил, их направления и точки приложения указаны в табл. С2; там же в столбце «Участок» указано, на каком участке действует распределенная нагрузка (например, в условиях №1 на конструкцию действуют сила  .под углом
.под углом  к горизонтальной оси, приложенная в точке L, сила
к горизонтальной оси, приложенная в точке L, сила  под углом 30° к горизонтальной оси, приложенная в точке E, и нагрузка, распределенная на участке СК).
под углом 30° к горизонтальной оси, приложенная в точке E, и нагрузка, распределенная на участке СК).
|
|
|
Таблица С2
| Силы
|
|
|
|
| Участок | ||||
|
|
|
|
| ||||||
| Номер условия | Точка приложения |

| Точка приложения |

| Точка приложения |

| Точка приложения |

| |
| 0 1 2 3 4 5 6 7 8 9 | K - L - L - E - - H | 60 - 15 - 30 - 60 - - 30 | - L - K - L - H K - | - 60 - 30 - 75 - 60 30 - | H - K - E - K L - - | 30 - 60 - -60 - 75 30 - - | - E - H - K - - E L | - 30 - 60 - 30 - - 15 60 | CL CK AE CL CK AE CL CK CL CK |
Определить реакции связей в точках A, В, С (для рис. 1, 2, 7, 9 еще и в точке D), вызванные заданными нагрузками. При окончательных расчетах принять а = 0,2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а.
|
|
|
| Участок на угольнике | Участок на стержне | ||
| горизонтальный | вертикальный | рис. 1,2,4,7,9 | рис. 0,3,5,6,8 |

| 
| 
| 
|
Таблица С2а
Указания. Задача С2 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы в целом, а затем – равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом аксиому (закон) о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен.
Пример С2. На угольник ABC ( 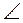 ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. С2а).
ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. С2а).

Рис. С2
Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена сила F, а к угольнику – равномерно распределенная на участке KB нагрузка интенсивности q и пара с моментом М.
Д а н о: f = 10 кН, М = 5 кНм, q = 20 кН/м, а = 0,2 м.
Определить: реакции в точках А, С, D, вызванные заданными .нагрузками.
Решение. 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. С2, б). Проведем координатные оси ху и изобразим действующие на стержень силы: силу F, реакцию N, направленную перпендикулярно стержню, и составляющие XD и УD о реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:
 , (1)
, (1)
 , (2)
, (2)
 . (3)
. (3)
2. Теперь рассмотрим равновесие угольника (рис. С2, в). На него действуют: сила давления стержня  , направленная противоположно реакции
, направленная противоположно реакции  , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой  , приложенной в середине участка KB (численно Q = =q·4a = 16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими ХA,YA, и пары с моментом МA. Для этой плоской системы сил тоже составляем три уравнения равновесия:
, приложенной в середине участка KB (численно Q = =q·4a = 16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими ХA,YA, и пары с моментом МA. Для этой плоской системы сил тоже составляем три уравнения равновесия:
 , (4)
, (4)
 , (5)
, (5)

 (6)
(6)
При вычислении момента силы  разлагаем ее на составляющие
разлагаем ее на составляющие 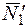 и
и  и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1) – (6), найдем искомые реакции. При решении учитываем, что численно
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1) – (6), найдем искомые реакции. При решении учитываем, что численно  в силу равенства действия и противодействия. Ответ: N = 2I,7 кН, YD = –10,8 кН, ХD = 8,8 кН, YA = =–26,8 кН, YA = 24,7 кН, MA = –42,6 кНм. Знаки указывают, что силы YD, ХA и момент МA имеют направления, противоположные показанным на рисунках.
в силу равенства действия и противодействия. Ответ: N = 2I,7 кН, YD = –10,8 кН, ХD = 8,8 кН, YA = =–26,8 кН, YA = 24,7 кН, MA = –42,6 кНм. Знаки указывают, что силы YD, ХA и момент МA имеют направления, противоположные показанным на рисунках.
Задача С3
Однородный стержень весом P = 24 Н прикреплен шарнирно к невесомым ползунам 1 и 2 (рис С3.0 – С3.9 табл. С3). Коэффициенты трения ползунов о направляющие, вдоль которых они могут скользить, равны соответственно f1 и f2 . К ползунам приложены силы Q1 и Q2, показанные на рисунках. Механизм расположен в вертикальной плоскости.
Определить величину, указанную в таблице в строке «Найти», где обозначено: 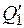 (или
(или  ) – наименьшее значение силы Q1 (или Q2), при котором имеет место равновесие;
) – наименьшее значение силы Q1 (или Q2), при котором имеет место равновесие;  (или
(или  ) – наибольшие значения тех же сил, при которых сохраняется равновесие;
) – наибольшие значения тех же сил, при которых сохраняется равновесие;  (или
(или 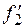 ) – наименьшее значение коэффициента трения, при котором сохраняется равновесие.
) – наименьшее значение коэффициента трения, при котором сохраняется равновесие.
Таблица С3
| Номер условия | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Q1, Н Q2, Н f1 f2 Найти | 60
-
0
0,2

| -
80
0,15
0

| 50
60
0
-
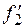
| 60
-
0,2
0

| -
80
0
0,15

| -
100
0,2
0
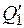
| 80
-
0
0,15

| 60
50
-
0

| -
100
0
0,2

| 80
-
0,15
0

|
Указания. Задача С3 – на равновесие тела под действием плоской системы сил при наличии трения скольжения. При решении задачи следует рассмотреть предельное положение равновесия, когда FТР = fN. Уравнения равновесия будут решаться проще, если их составить в виде уравнений моментов относительно точек, где пересекаются линии действия двух неизвестных сил (вместо одного из таких уравнений можно составить уравнение проекций на ось, перпендикулярную неизвестной силе).
Условие f1 = 0 (или f2 = u) означает, что ползун 1 (или 2) гладкий; соответствующую силу трения на чертеже не изображать и в уравнения не вводить (введение этой силы с тем, чтобы потом положить j = =0, сильно усложнит решение).
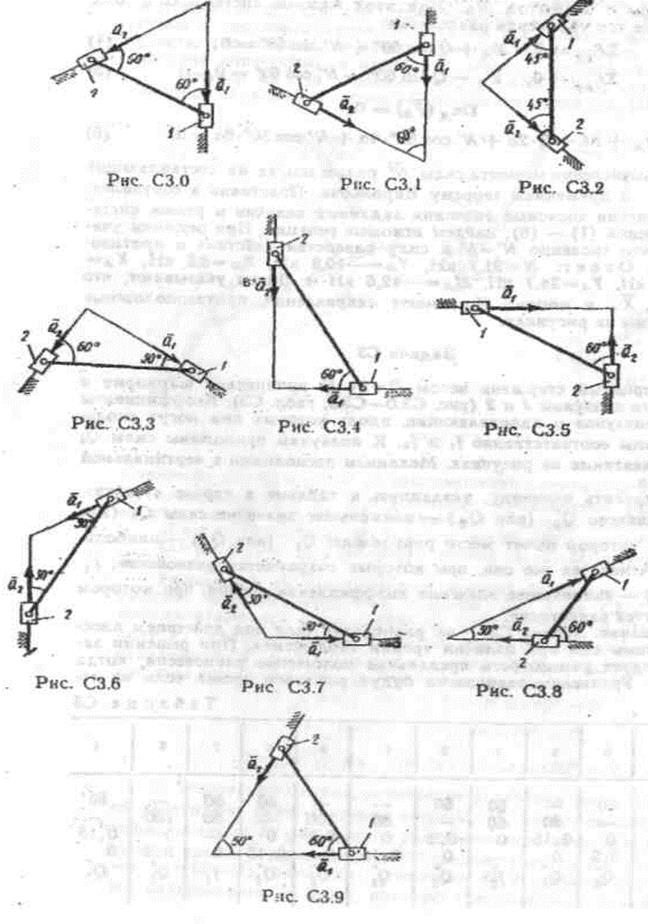
Пример С 3 . Жесткий угольник ADB весом Р (  ADB = 90°), расположенный в вертикальной плоскости, прикреплен шарнирами к ползунам 1 и 2 (рис. С3). Линия действия силы
ADB = 90°), расположенный в вертикальной плоскости, прикреплен шарнирами к ползунам 1 и 2 (рис. С3). Линия действия силы  проходит на расстоянии h от стороны AD, В середине стороны AD приложена горизонтальная сила Q. Коэффициент трения ползуна 1 о направляющие равен f1, ползун 2 гладкий.
проходит на расстоянии h от стороны AD, В середине стороны AD приложена горизонтальная сила Q. Коэффициент трения ползуна 1 о направляющие равен f1, ползун 2 гладкий.

Рис. С3
Дано: Р = 40 Н, BD = b = 0,8 м, h = 0,3 м, а = 0,2 м, f1, = 0,3. Угол между направляющими 120°.
Определить: 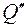 – наибольшее значение силы Q, при котором сохраняется равновесие.
– наибольшее значение силы Q, при котором сохраняется равновесие.
Решение. 1. Рассмотрим предельное равновесие угольника, при котором Q = 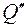 . Изображаем действующие на угольник силы P, Q, нормальные реакции N1, N2 и предельную силу трения FТР приложенную к ползуну 1.
. Изображаем действующие на угольник силы P, Q, нормальные реакции N1, N2 и предельную силу трения FТР приложенную к ползуну 1.
То, что сила Q имеет наибольшую возможную величину, означает, что при ее дальнейшем увеличении равновесие нарушится и под действием силы Q ползун 1 начнет скользить влево, а ползун 2 – вверх. Следовательно, при равновесии сила FTP, удерживающая ползун 1 от скольжения влево, направлена вправо (направление силы FTP при решении подобной задачи надо обязательно установить и показать это направление на рисунке верно).
2. Так как сила трения, выражающаяся через нормальную реакцию, действует лишь на ползун 1, то реакцию N2 можно не определять и составить только два уравнения равновесии, в которые N2 не войдет. Для этого проведем сначала линии действия неизвестных реакций N1 и N2 до их пересечения в точке Е и составим уравнение  , в которое N1 и N2 не войдут. Получим, полагая Q =
, в которое N1 и N2 не войдут. Получим, полагая Q = 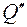 :
:
 , (1)
, (1)
где DE = b tg30  = 0,46 м. Тогда при заданных значениях h и а уравнение (1) примет вид
= 0,46 м. Тогда при заданных значениях h и а уравнение (1) примет вид
 ,
,
откуда находим
 . (2)
. (2)
Равенство (2) не может дать FTP < 0, поскольку направление силы FTP было заранее установлено и показано на рис. С3 верно. Следовательно, должно быть
 > 0,35Р или
> 0,35Р или  > 0,45Р. (3)
> 0,45Р. (3)
Для определения N1, можно составить или уравнение моментов относительно точки, где пересекаются линии действия сил N2 и FTP, или уравнение проекций на ось, перпендикулярную N2. Составим, проведя ось Вх, уравнение  . Получим
. Получим
 . (4)
. (4)
Отсюда, заменяя FTP его значением (2), найдем окончательно;
 . (5)
. (5)
Для определения  учтем, что когда равновесие является предельным, то FTP и N1 связаны соотношением
учтем, что когда равновесие является предельным, то FTP и N1 связаны соотношением
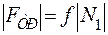 (6)
(6)
Подчеркиваем, что в это равенство входят модули сил. В нашем случае |FTP |= FTP, так как было установлено, что
FTP > 0 и дается равенством (2). Но утверждать, что в равенстве (5) N1 > 0 нет оснований, так как направление N1, может быть и противоположно показанному на рис. С3. Поэтому рассмотрим оба возможных случая:
а)N1 > 0 (реакция N1 направлена так, как показано на рис. С3). Тогда, подставляя в (6) значения FTP и N1 из (2) и (5) и учтя, что f = 0,3, получим
 ,
,
откуда находим
 Н. (7)
Н. (7)
б)  (направление N1 противоположно показанному на рис. С3). Тогда
(направление N1 противоположно показанному на рис. С3). Тогда  и равенство (6) дает
и равенство (6) дает
 ,
,
откуда
 Н. (8)
Н. (8)
Из полученных результатов (7) удовлетворяет неравенству (3), а (8) не удовлетворяет. Следовательно, окончательный ответ будет  H.
H.
Примечания:
1. Если в задаче требуется найти наименьшее значение Q' силы Q, при котором сохраняется равновесие, то это означает, что при дальнейшем уменьшении силы Q она не удержит угольник в равновесии и под действием силы P ползун 2 начнет скользить вниз, а ползун 1 – вправо; следовательно, в этом случае сила FТР, удерживающая ползун 1 от скольжения вправо, будет направлена влево (противоположно показанной на рис. С3). В остальном весь ход решения остается таким же, как в рассмотренном примере.
2. Если в задаче все действующие силы заданы и надо найти наименьший коэффициент трения:  , при котором сохраняется равновесие, то силу FТР (как и реакции) можно направлять в любую сторону и, составив уравнения равновесия, аналогичные, например, уравнениям (1) и (4) в рассмотренном примере, найти из них FТР и N1. При этом, поскольку действующие силы заданы, для FТР и N1 получатся конкретные числовые значения. Эти значения и следует подставить в равенство (6) и найти из него
, при котором сохраняется равновесие, то силу FТР (как и реакции) можно направлять в любую сторону и, составив уравнения равновесия, аналогичные, например, уравнениям (1) и (4) в рассмотренном примере, найти из них FТР и N1. При этом, поскольку действующие силы заданы, для FТР и N1 получатся конкретные числовые значения. Эти значения и следует подставить в равенство (6) и найти из него  . Если при расчетах получится FТР < 0 или N1 < 0, то это означает лишь, что направление соответствующей силы противоположно показанному на рисунке, но результат не изменится, так как в (6) входят модули сил.
. Если при расчетах получится FТР < 0 или N1 < 0, то это означает лишь, что направление соответствующей силы противоположно показанному на рисунке, но результат не изменится, так как в (6) входят модули сил.
Задача С4
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам А, В, С, D (рис. С4.0 – С4.9, табл. С4). Стержни и узлы (узлы расположены в вершинах H, К, L или М прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила P = 200 Н; во втором узле приложена сила Q = 100 H. Сила P образует с положительными направлениями координатных осей x, y, z углы, равные соответственно  , а сила Q – углы
, а сила Q – углы  направления осей x, y, z для всех рисунков показаны на рис. С4.0.
направления осей x, y, z для всех рисунков показаны на рис. С4.0.
Грани параллелепипеда, параллельные плоскости ху, – квадраты. Диагонали других (боковых) граней образуют с плоскостью ху угол  , а диагональ параллелепипеда образует с этой плоскостью угол
, а диагональ параллелепипеда образует с этой плоскостью угол  . Определить усилия в стержнях.
. Определить усилия в стержнях.
На рис. С4.10 в качестве примера показано, как должен выглядеть чертеж С4.3, если по условиям задачи узлы находятся в точках L и М, а стержнями являются LM, LA, LB; MA, MC, MD. Там же показаны углы 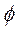 и
и  .
.
Указания. Задача С4 – на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть аксиому (закон) о равенстве действия и противодействия; начинать с узла, где сходятся три стержня. Изображать чертеж можно без соблюдения масштаба, так чтобы лучше были видны все 6 стержней. Стержни следует пронумеровать, в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, N1, N2 и т. д.).
Таблица С4
| Номер условия | 0 | 1 | 2 | 3 | 4 |
| Узлы | H, M | L, M | K, M | L, H | K, H |
| Стержни | HM, HA HB, MA MC, MD | LM, LA LD, MA MB, MC | KM, KA KB, MA MC, MD | LH, LC LD, HA HB, HC | KH, KB KC, HA HC, HD |
| Номер условия | 5 | 6 | 7 | 8 | 9 |
| Узлы | M, H | L, H | K, H | L, M | K, M |
| Стержни | MH, MB MC, HA HC, HD | LH, LB LD, HA HB, HC | KH, KC KD, HA HB, HC | LM, LB LD, MA MB, MC | KM, KA KD, MA MB, MC |


Пример С4. Конструкция состоит из невесомых стержней 1, 2, ...., 6, соединенных друг с другом (в узлах К и М) не неподвижными опорами А, В, С, D шарнирами (рис. С4). В узлах К и M приложены силы Р и Q, образующие с координатными осями углы  соответственно (на рисунке показаны только углы
соответственно (на рисунке показаны только углы  ).
).
Дано: 
 .
.
Определить: усилия в стержнях 1 – 6.

Рис. С4
Решение. 1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. На узел действуют сила Р и реакции N1, N2, N3 стержней, которые направим по стержням от узла, считая стержни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:
 , (1)
, (1)
 , (2)
, (2)
 . (3)
. (3)
Решив уравнения (1), (2), (3) при заданных числовых значениях силы Р и углов, получим: N1 = 349 Н, N2 = 345 Н, N3 = 141 Н.
2. Рассмотрим равновесие узла М. На узел действуют сила Q и реакции  ,
,  ,
,  ,
,  стержней. При этом по закону о равенстве действия и противодействия реакция N'2 направлена противоположно
стержней. При этом по закону о равенстве действия и противодействия реакция N'2 направлена противоположно  , численно же
, численно же  . Составим уравнения равновесия:
. Составим уравнения равновесия:
 , (4)
, (4)
 , (5)
, (5)
 . (6)
. (6)
При определении проекций силы  на оси x и y в уравнениях (4) и (5) удобнее сначала найти проекцию
на оси x и y в уравнениях (4) и (5) удобнее сначала найти проекцию  этой силы на плоскость xOy (по величине
этой силы на плоскость xOy (по величине  ), а затем найденную проекцию на плоскость спроектировать на оси.
), а затем найденную проекцию на плоскость спроектировать на оси.
Решив систему уравнений (4), (5), (6) и учитывая, что  Н, найдем, чему равны N4, N5, N6.
Н, найдем, чему равны N4, N5, N6.
Ответ: N1 = 349 Н, N2 = –345 Н, N3 = 141 Н, N4 = 50 H, N5 = =329 H, N6 = –66 Н. Знаки показывают, что стержни 2 и 6 сжаты, остальные – растянуты.
Задача С5
Две однородные прямоугольные тонкие плиты, сваренные под прямым углом друг к другу, закреплены сферическим шарниром (или подпятником) в точке A, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С5.0–С5.7) или же двумя подшипниками в точках А и В и двумя невесомыми стержнями 1 и 2 (рис. С5.8, С5.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
Размеры плит в направлениях, параллельных координатным осям x, y, z, равны соответственно или 2а, 3а и а (рис. 0–4), или 2а, 3а, 4а (рис. ,5–9); вес большей плиты P1 = 3 кН, вес меньшей плиты P2 = 2 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху горизонтальная).
На плиты действуют пара сил с моментом M = 4 кНм, лежащая в плоскости одной из плит, и две силы. Величины этих сил, их направления и точки приложения указаны в табл. С5; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости ху, сила F2 в плоскости, параллельной xy, и сила F3 в плоскости, параллельной yz. Точки приложения сил (D, Е, Н, К) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а = 0,6 м.
Таблица С5
| Силы |
|
|
|
| ||||
| Номер условия | F1 = 6 кН | F2 = 8 кН | F3 = 10 кН | F4 = 12 кН | ||||
| Точка приложения | 
| Точка приложения | 
| Точка приложения | 
| Точка приложения | 
| |
| 0 | E | 60 | H | 30 | - | - | - | - |
| 1 | - | - | D | 60 | E | 30 | - | - |
| 2 | - | - | - | - | K | 60 | E | 30 |
| 3 | K | 30 | - | - | D | 0 | - | - |
| 4 | - | - | E | 30 | - | - | D | 60 |
| 5 | H | 0 | K | 60 | - | - | - | - |
| 6 | - | - | H | 90 | D | 30 | - | - |
| 7 | - | - | - | - | H | 60 | K | 90 |
| 8 | D | 30 | - | - | K | 0 | - | - |
| 9 | - | - | D | 90 | - | - | H | 30 |


Указания. Задача С5 – на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) – две составляющие; лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы  часто удобно разложить ее на две составляющие
часто удобно разложить ее на две составляющие  и
и 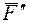 , параллельные координатным осям (или на три); тогда по теореме Вариньона
, параллельные координатным осям (или на три); тогда по теореме Вариньона  и т. д.
и т. д.

Рис. С5
Пример С5. Горизонтальная прямоугольная плита весом Р (рис. С5) закреплена сферическим шарниром в точке А, цилиндрическим подшипником в точке В и невесомым стержнем DD '. На плиту в плоскости, параллельной xz, действует сила  , а в плоскости, параллельной xz, – пара сил с моментом M.
, а в плоскости, параллельной xz, – пара сил с моментом M.
Дано:
 : •
: •
Определить: реакции опор А, В и стержня DD '.
Решение. 1. Рассмотрим равновесие плиты. На плиту действуют заданные силы  ,
,  и пара с моментом М, а также реакции связей.
и пара с моментом М, а также реакции связей.
Реакцию сферического шарнира разложим на три составляющие  ,
,  ,
,  , цилиндрического подшипника – на две составляющие
, цилиндрического подшипника – на две составляющие  ,
,  (в плоскости, перпендикулярной оси подшипника); реакцию
(в плоскости, перпендикулярной оси подшипника); реакцию 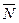 стержня направляем вдоль стержня от D к D ', предполагая, что он растянут.
стержня направляем вдоль стержня от D к D ', предполагая, что он растянут.
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
 ; (1)
; (1)
 ; (2)
; (2)
 ; (3)
; (3)
 ; (4)
; (4)
 ; (5)
; (5)
 .(6)
.(6)
При определении моментов силы 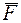 относительно осей разлагаем ее на составляющие
относительно осей разлагаем ее на составляющие  и
и  , параллельные осям x и y (
, параллельные осям x и y (  ,
,  ), и применяем теорему Вариньона (см. Указания). Аналогично можно поступить при определении моментов реакции
), и применяем теорему Вариньона (см. Указания). Аналогично можно поступить при определении моментов реакции  .
.
Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.
Ответ: 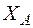 = 3,4 кН,
= 3,4 кН,  = 5,1 кН,
= 5,1 кН,  = 4,8 кН,
= 4,8 кН,  = –7,4кН,
= –7,4кН,  = 2,1 кН, N = 5,9 кН. Знак минус указывает, что реакция
= 2,1 кН, N = 5,9 кН. Знак минус указывает, что реакция  имеет направление, противоположное показанному на рис. С5.
имеет направление, противоположное показанному на рис. С5.
Задача С6
Плоское тело состоит из четырех (либо из трех) квадратов I-IV (рис. С6) со стороной R и двух из трех элементов, изображенных на рис. С6-1, С6-2, С6-3. Число квадратов, входящих в тело, и их номера указаны во втором столбце таблицы С6. Номер строки, указывающей номера квадратов I-IV, определяется из первого столбца таблицы С6 и этот номер совпадает с предпоследней цифрой шифра. Номер строки, указывающей элементы, присоединяемые к квадратам, берется так же из первого столбца таблицы С6, и этот номер совпадает с последней цифрой шифра. В таблице С6 в столбцах элементы 1, 2 и 3 указывается, какая сторона элемента совпадает с соответствующей стороной одного из квадратов при параллельном переносе элементов до совпадения указанных сторон.
Элемент 1 (рис. С6-1) – равнобедренный прямоугольный треугольник со сторонами  . Элемент 2 (рис. С6-2) представляет собой часть площади квадрата со стороной R, из которого вырезана четверть круга радиуса R. Элемент 3 (рис. С6-3) – четверть круга радиуса R.
. Элемент 2 (рис. С6-2) представляет собой часть площади квадрата со стороной R, из которого вырезана четверть круга радиуса R. Элемент 3 (рис. С6-3) – четверть круга радиуса R.

Если площадь присоединяемого к квадратам элементов 1-3 не совпадает с имеющейся уже площадью квадратов I-IV, то это дополнительная площадь тела; если совпадает, то площадь присоединяемого элемента есть отверстие в квадрате. Определить координаты центра тяжести однородного плоского тела.
Указания. Задача С6 – на определение координат центров тяжести однородных плоских тел. Тело разбивается на отдельные тела, координаты центров тяжести которых известны: квадраты, прямоугольники, треугольники, секторы. Координаты центров тяжести плоских тел определяются по формулам
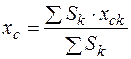 ;
; 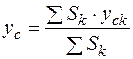 ,
,
где  – площадь k-того тела;
– площадь k-того тела;  – координаты центра тяжести k-того элемента тела;
– координаты центра тяжести k-того элемента тела; 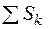 – площадь тела.
– площадь тела.
Таблица С6
| Номера рисунков и элементов | Квадрат (рис. 6) | Элементы | |||
| 1 | 2 | 3 | |||
| 0 | I, II, III, IV | D1B1→AO | P2b→PB | - | |
| 1 | I, II, III, IV | D1B1→AO | P2b→AK | - | |
| 2 | I, II, III, IV | A1B1→PB | - | aO3→BS | |
| 3 | I, II, III, IV | A1B1→PB | - | aO3→ON | |
| 4 | I, II, III | D1B1→KN | P2b→BS | - | |
| 5 | I, II, III | D1B1→KN | P2b→KD | - | |
| 6 | I, II, III | D1B1→KN | - | O3b→PA | |
| 7 | I, II, III | D1B1→KN | - | aO3→NV | |
| 8 | I, II, III | D1B1→KN | aP2→KS | - | |
| 9 | I, II, III, IV | D1B1→BK | - | aO3→NV | |
При решении задачи можно воспользоваться методом отрицательных площадей: тело с отверстием можно рассматривать как тело без отверстия и отдельно тело, площадь которого равна площади отверстия, но отрицательная. При рациональном решении задачи число элементов, на которые разбивается плоское тело, должно быть минимальным.
Оси координат, относительно которых определяются координаты центров тяжести тел, указаны на рис. С6. После присоединения к квадратам I-IV элементов 1-3 внешний контур полученного тела обвести более толстой линией.
Пример С6. Плоское тело (рис. С6–4) состоит из четырех квадратов I, II, III, IV (рис. С6) со стороной R. На квадрат II наложен элемент 2 (рис. С6–2), который рассматривается как отверстие в квадрате II. К квадрату III присоединена четверть круга радиуса R (элемент 3, рис. С6–3), а к квадрату IV – треугольник (элем. 1, рис. С6–1). Определить: координаты 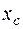 и
и  полученного плоского тела.
полученного плоского тела.
Решение. Разбиваем тело (рис. С6–4) на тела, координаты центров тяжести которых известны. Определяем площадь  и координаты
и координаты  и
и  каждого элемента.
каждого элемента.
1. Прямоугольник DADV. Его центр тяжести С1 находится на пересечении диагоналей

Площадь  ;
;  ,
,  .
.
2. Квадрат APBK
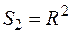 ;
;  ,
,  .
.
3. Треугольник B1D1A1.
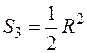 ; центр тяжести треугольника С3 находится в точке пересечения его медиан. Так как медианы точкой их пересечения делятся на части
; центр тяжести треугольника С3 находится в точке пересечения его медиан. Так как медианы точкой их пересечения делятся на части  и
и  , то
, то  ,
,  .
.
4. Четверть круга  .
.
 . Центр тяжести С4 однородного сектора лежит на биссектрисе центрального угла. Причем отрезок SC4 определяется выражением:
. Центр тяжести С4 однородного сектора лежит на биссектрисе центрального угла. Причем отрезок SC4 определяется выражением:
 , где
, где 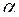 – половина центрального угла
– половина центрального угла  (в знаменателе
(в знаменателе  – в радианах). В данной задаче
– в радианах). В данной задаче 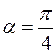 . Получаем
. Получаем
 .
.
Тогда координаты центра тяжести С4 равны
 ;
;
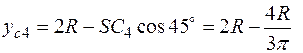 .
.
5. Четверть круга O3ab. По аналогии с четвертым элементом
 ,
,  ;
;
 .
.
Координаты центра тяжести тела точки С (рис. С6-4) определяется по формулам:






Ответ:  ;
;  . Указываем центр тяжести тела на рис. С6–4.
. Указываем центр тяжести тела на рис. С6–4.
Дата добавления: 2019-03-09; просмотров: 3514; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



 =10 кН
=10 кН =20 кН
=20 кН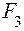 =30 кН
=30 кН =40 кН
=40 кН

 =10 кН
=10 кН =30 кН
=30 кН


