Оценка параметров модели Брауна

⇐ ПредыдущаяСтр 5 из 5

t	y_t	a₀	a₁
0		16,68	10,48
1	27,3	27,231	10,493	27,160	0,140	0,513
2	41.8	39,803	10,859	37,724	4,076	9,751
3	42,8	46,652	10,152	50,662	-7,862	18,370
4	56,2	56,496	10,097	56,804	-0,604	1,075
5	72,5	69,606	10,629	66,594	5,906	8,147

32	418,1	419,625	6,628	421,213	-3,113	0,744
33	424,6	425,410	6,479	426,254	-1,654	0,389
34	435,1	433,527	6,768	431,890	3,210	0,738
35	439,8	440,043	6,724	440,295	-0,495	0,113

5) По модели со скорректированными параметрами а_0(t) ходим прогноз на следующий момент времени t = 1, t = 2:

Возврат к пункту 3.

Вычисления повторяем до конца наблюдений.

6) Параметры модели, полученные в последний момент времени (t = 35), используем для построения прогноза на три недели вперед (t = 1, 2, 3);

Результаты прогнозирования по модели Брауна представлены графически на рис. 5.1.

Рис. 5.1. Исходные данные, результаты моделирования (альфа = 0,3) и точечный прогноз

В моделях Брауна и Хольта параметры сглаживания характеризуют степень адаптации модели к изменению ряда наблюдений. Они определяют скорость реакции модели на изменения, происходящие в развитии. Чем они больше, тем быстрее реагирует модель на изменения. Обычно для устойчивых рядов их величина большая, а для неустойчивых - маленькая. В различных методах прогнозирования используется различный подход к их определению. Их можно взять фиксированными, а наилучшее значение определить методом подбора, чтобы ошибка прогноза на один шаг вперед была наименьшей. При использовании компьютера это не представляет труда. Альтернативу этому подходу составляет динамическое изменение параметров сглаживания. В методах эволюции и симплекс-планирования параметры адаптации постоянно меняются на каждом шаге. Для каждого параметра сглаживания формируется несколько значений.

Модели и методы авторегрессии

Авторегрессионные модели широко используются для описания стационарных случайных процессов. Характерной особенностью стационарных временных рядов является то, что их вероятностные свойства рядов не изменяются во времени. Иначе говоря, функции распределения стационарных динамических рядов не меняются при сдвиге времени.

Модель, в которой расчетные значения уровней ряда определяются как линейная функция от предыдущих наблюдений, называют авторегрессионной. Если текущая величина уровня ряда у_t зависит только от одного предшествующего значения у_t-1 то такая модель является авторегрессионной моделью первого порядка АР (1), если у_t, зависит от двух предшествующих уровней у_t-1, и у_t-2, моделью второго порядка АР (2) и т.д. до порядка р, т.е. АР (р).

Если АР-модель имеет первый (р = 1) или второй порядок (р = 2), то она приобретает соответственно следующий вид:

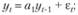
Идентификация АР(р) модели состоит в определении ее порядка р. Одной из предпосылок построения модели этого типа является применение их к стационарному процессу. Поэтому в более широком смысле идентификация модели включает также выбор способа трансформации исходного ряда наблюдений, как правило, имеющего некоторую тенденцию, в стационарный (или близкий к нему) ряд. Один из наиболее распространенных способов решения этой проблемы - последовательное взятие разностей, т.е. переход от исходного ряда к ряду первых, а затем и вторых разностей.

"Чистые" авторегрессионные процессы имеют плавно затухающую автокорреляционную функцию (АКФ). В этом случае в качестве порядка модели выбирается лаг, после которого все частные автокорреляционные функции (ЧАКФ) имеют незначительную величину. Однако на практике редко встречаются процессы, которые легко было бы идентифицировать. Поэтому порядок модели обычно определяется методом проб из нескольких альтернатив. В число кандидатов включаются модели, у которых порядок соответствует ЧАКФ, превышающей стандартное отклонение 1/N. При обработке разностных рядов иногда ориентируются на АКФ, выбирая модели, у которых порядок соответствует максимальному ее значению, при условии, что оно превышает стандартное отклонение.

Ряды без тенденции, как правило, не представляют интереса для экономистов. АР-модели вообще не предназначены для описания процессов с тенденцией, однако они хорошо описывают колебания, что весьма важно для отображения развития неустойчивых показателей.

Чтобы применить АР-модели к экономическим процессам с тенденцией, на первом этапе формируют стационарный ряд, исключая тенденцию, путем перехода от исходного ряда к ряду разностей соседних значений членов ряда. Например, переход от исходного ряда y_t(t =1,2,..., п) к ряду ∆y_t(t =1,2,..., п - d) первых (d = 1) или вторых (d = 2) разностей осуществляется следующим образом:

t = 1, 2,..., п при d = 0;

t= 1,2,..., п - 1 при d = 1;

t = 1,2,..., п - 2 при d = 2.

Первоначальный (исходный) ряд является интегрированным рядом первого порядка, когда его первые разности образуют стационарный ряд динамики. Если для формирования стационарного временного ряда требуется получить ряд вторых разностей, то исходный ряд называется интегрированным рядом второго порядка и т.д.

После перехода к разностным рядам авторегрессионная модель порядка т первых разностей (приростов) и вторых разностей приобретает соответственно такой вид:

Таким образом, АР-модели разностных временных рядов характеризуются двумя параметрами: р (порядок авторегрессии) и d (порядок конечных разностей), поэтому записываются как АР (р, d).

Простейшим способом определения наиболее подходящего разностного ряда является вычисление для каждого ряда (d = 0, 1, 2) его дисперсии. Для дальнейшей обработки выбирается ряд, у которого величина этого показателя минимальна.

Для идентификации порядка модели может быть использована частная автокорреляционная функция. Если для т лагов частные коэффициенты автокорреляции статистически значимы, а затем для лагов т + 1 и далее резко падают до нулевого значения, то это указывает на авторегрессионный процесс порядка т.

При моделировании нестационарных по своей природе экономических процессов авторегрессионная функция объединяется с другими методами анализа динамики: скользящей средней, трендом, сезонной волной. Объединение разных моделей в единое целое существенно расширяет сферу их использования.

Построение моделей авторегрессии и получение прогнозных оценок исходного ряда возможно только с использованием программных средств. При грамотном использовании хорошие результаты дает модель Бокса - Дженкинса.

Данную модель также называют авторегрессионной интегрированной моделью скользящего среднего или сокращенно АРИСС (р, d, q).

При построении АРИСС-моделей с использованием программных средств осуществляются:

а) идентификация динамического ряда (определение размерности операторов конечной разности d, авторегрессии р и скользящего среднего q);

б) оценивание параметров модели;

в) проверка адекватности модели.

Пример 5.4. Рассмотрим построение прогноза объема продаж с использованием программы SPSS.

В результате расчетов в качестве лучшей выбрана модель ARIMA (1, 1, 0). Ниже в табл. 5.8 и 5.9 приведены расчеты построения прогноза объема продаж, выполненные с использованием программы SPSS. На рис. 5.2 представлены результаты аппроксимации и прогнозирования по этой модели. Построенная модель характеризуется высоким коэффициентом детерминации 0,986 и низким значением средней относительной ошибки аппроксимации 6,48%.

Таблица 5.8

Параметры модели АРПСС

					Оценка	Стандартная ошибка	t	Знач.
Y-Модель_1	Y	Нет преобразования	Константа		12,175	2,144	5,679	,000
			АР	Лаг 1	-,390	,162	-2,400	,022
			Дифференцирование		1

Таблица 5.9

Дата добавления: 2019-03-09; просмотров: 318; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 45

Мы поможем в написании ваших работ!